高中生对圆锥曲线的学习现状及问题分析
孙艳婷 李云飞


【摘 要】 “圆锥曲线”内容是高中数学十分重要的一部分,在数学知识的体系中起着承上启下的作用,不仅在高中学习以及高考中占据一定的地位,与我们的日常生活也紧密相关.可对于这部分知识,学生们的得分往往不尽人意,那么高中生对圆锥曲线问题的学习现状究竟如何呢?为此,笔者对部分高中生开展了圆锥曲线认知水平的调查.
【关键词】 圆锥曲线;高中数学;学习现状
1 研究背景
1.1 圆锥曲线在高中数学教学中的重要性
1.1.1 “圆锥曲线”在高中数学课程中的重要性
“圆锥曲线”是苏教版高二数学选择性必修第一册(2019版)第3章的内容,在整个高中数学学习的过程中起着十分重要的作用.首先,对于高二的学生来说,在初中时期就已经接触到了关于求解直线与圆的问题,在初中的基础上,高中阶段对这部分知识进行了进一步的拓展与加深,学生此时已经具备了一定的数学抽象思维的能力,在这个阶段进行圆锥曲线的学习,学生既可以同化之前所学习过的知识,又为后续解决一些解析几何综合应用的问题起到铺垫作用,进一步完善关于解析几何问题的解决方法,为学生之后学习空间解析几何打下良好的基础.
1.1.2 “圆锥曲线”蕴含着数学核心素养
圆锥曲线整个模块的核心思路是希望借助直线与圆锥曲线方程的代数关系,研究几何问题,这就构建了极强的数与形的对应关系.需要我们学会运用数形结合的思想、函数与方程的思想、转化与化归思想和分类讨论思想.学习圆锥曲线这部分知识时,必然要涉及到直线与曲线方程联立解题,而这就需要培养学生的直观想象能力,在具体解体的的过程中,也要加强学生的运算能力[1HYPERLINK\l"_ENREF_1"\o"张鑫萌,2020#21"].学生要能够发现已有知识和新知识之间的联系,从而逐渐发现学习数学的乐趣,将枯燥的数学学习转化为获取新知并成功解决问题的动力,教师更要引导学生形成解决问题的思路,加深学生对事物本质和发展规律的理解和认知.
1.1.3 “圆锥曲线”的广泛应用
“圆锥曲线”不仅仅在高中数学课程中有着极其重要的地位,在其他的领域中也有着举足轻重的作用,比如物理学中的天体运动问题,也常常需要用到圆锥曲线的数学知识和方法来解决物理问题,还有实际生活中的建筑,如发电厂冷却塔的外形线等的问题也经常要用到圆锥曲线相关知识来解决.由此可见,通过学习圆锥曲线知识既可以解决数学问题,又可以帮助解决实际自然生活以及物理学问题.
1.2 《课标》以及考纲对圆锥曲线部分的要求
2017 年国家教育部颁发的《普通高中数学课程标准》中,圆锥曲线属于几何与代数这一主线,是平面解析几何的核心内容.笔者根据《普通高等学校招生全国统一考试大纲的说明》和《课标》对圆锥曲线知识的要求,将此以表格形式呈现出来:
2 高中生对圆锥曲线的学习现状调查研究
2.1 调查方法
此次调查的方法采用的是:普遍调查的方法[2HYPERLINK\l"_ENREF_2"\o"何西,2018#17"].此次考试本年级共有698名学生参加测试,采取一份试卷两人阅评的方式,高二的教研组的13名教师中批改圆锥曲线试题的共有3名,分值误差在2分以上是将采取第三轮评卷以保证学生分数的公平性和准确性.系统会根据学生的分数进行归类和统计,从而得出科学的依据.
2.2 调查背景
此次调查是对高二学生的阶段性测试,其中圆锥曲线占比50%左右,有关圆锥曲线考题单选题为第4、5、6、7、8 ,多选题为10、11、12题,解答题为18、22题.此次我选择理科实验1班、理科普通3班、文科实验5班、文科普通6班作为调查对象,具体情况如下:
以上是江苏省某市2020届高二学生第一次月考成绩整理得到的数据.
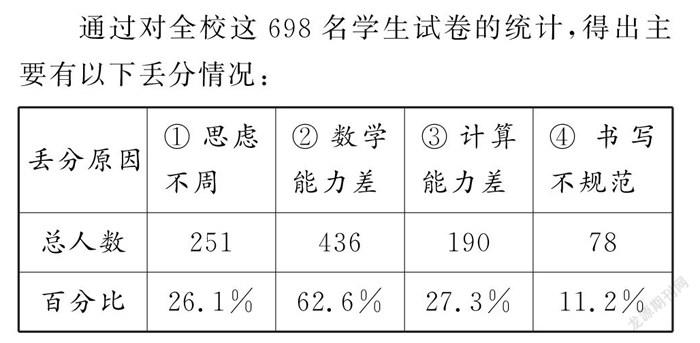
通过对全校这698名学生试卷的统计,得出主要有以下丢分情况:
通过对以上数据的分析,不难发现要想使学生在圆锥曲线部分少丢分,必须要从以上几方面入手,找出问题最根本所在.
(1)忽略题目中关键条件以及不能准确分析中解题的关键要素(思虑不周)
解决此题的重要思路是通过数形结合的思想先将直线方程与椭圆方程进行联立,再通过跟与系数关系,结合图形,完成从形到数的转化进而将问题解决.在解题时忽略了已知条件,未能分析解题的关键要素从而失分.
(2)没能掌握圆锥曲线定义,“数形结合”能力以及解题策略差(数学能力差)
圆锥曲线重点考察数形结合能力,不能考虑到将直线与方程进行联立解题说明并没有掌握圆锥曲线真正的考察内容,缺失了数形结合的思想从而导致失分.
(3)复杂计算不敢算或计算错误(计算能力差)
学生对于计算能力的掌握实际上一直是弱项,在整个数学学习的过程中,没有大量的练习,是不可能有突破性的进步和提升的,在圆锥曲线的学习中,此方面处于弱势的同学会表现得更加明显,除了大量的练习以外还需要学生的细心和耐心,在高压强度的学习下,要想学生能有此认真平稳的态度,这并非易事.
(4)书写不公正卷面不清晰以及笔记勾连(书写不规范)
卷面整潔是考试中获得优胜必不可少的一部分.
3 提高学生生对圆锥曲线的学习能力的教学策略
我们把得分在120分及以上同学作为优秀生,90-120分之间的同学作为普通生,0-90分之间的同学作为困难生.通过对抽调的试卷分析以及对不同程度的学生的得分情况来看,得出了学生在圆锥曲线失分的主要地方,根据学生试卷反映情况以及数据的统计分析,我们得出了以下几方面解决策略.
3.1 培养数形结合思想,有策略有方法的解决问题
数学解题思维是学生在解决问题时的重要突破点,也是数学教师口中经常强调的.做题要有一定的逻辑顺序,同时也要因人而异,找到属于自己的一套方式方法.每个同学解题的切入点不同,所体现出的解题思维自然有所区别.能否形成数学思维,要靠平时的训练与培养.因此在学习圆锥曲线的过程中,教师作为教育的主导者,要潜移默化的引导学生发散思维,在不断地练习中培养学生的数形结合能力,将思想作为指导,方法作为实施策略,是解决数学问题的有效方法.
通过调查也能看出:学生在解决问题的主要影响因素有:(1)数学语言转化意识不足,不能很好的理解题目;(2)“数”与“形”之间转化能力弱,不能根据题中所给信息制定一个可执行的解题策略;(3)有时尽管是正确的方向却由于未检验或漏掉重要信息而导致解题失败.
数学思想是数学的灵魂,应该培养学生多元表征数学问题的能力,这需要学生有清晰的解题方案和方法步骤.数学不单单是一门“计算”的学科,在解决问题的过程中多方面培养人的思维的有序性,逻辑的缜密性才是学习的最终目的.波利亚的解题研究在这方面可以给我们提供很好的理论支撑以及可实施的具体方法.
(1)理解题目:确定未知量、数据、条件以及舍去题目中的多余部分.
(2)拟定方案:找出已知数据与未知量之间的联系,观察未知量,回忆曾经解过的与其相似的题目或引入某个辅助元素从而拟定一套可执行的方案,此时就要拥有一定的数形结合能力作为解题的依据.
(3)执行方案:执行解题方案并检查每一个步骤.
(4)回顾:检验已经得到的回答,此时可以从解出的具体数值带回已知条件,图形也可以帮助我们进行检验判断.
将这一解题策略具体运用到学生解决圆锥曲线的过程中,不仅可以加强他们对已知与未知之间的联系,巩固深化脑中已有的知识,再建立起旧知识与新知识之间的桥梁,将完整的解题策略反复熟练运用会显著提高学生的数学能力.
3.2 加强学生对知识的运用、掌握归纳的结论
很多的同学在做解析几何时,书写的很繁琐,尤其是对于圆锥曲线一些常见的二级结论陌生,甚至根本不了解.教师要在此时发挥主导作用,不仅要将一些常见圆锥曲线的二级结论给学生推导整理,更要让他们熟记于心.在解题过程中即使不能熟练运用至少也要能自己推导出来所需要的公式或做题方法,掌握后常加以运用,熟能生巧说的也是这个道理.
3.3 提高学生的运算能力
数学运算是由低级到高级、由简单到复杂、由具体到抽象的过程,这就决定了数学运算具有层次性,只有简单的、低级的、具体的运算过了关,才能进行深层次的复杂、高级、抽象运算.如果简单的基本运算技能都没能掌握,那么复杂的运算学生更无法解决[3HYPERLINK\l"_ENREF_3"\o"石伟娜,2016#19"].所以,在实际教学中,教师要注重学生有关运算的基础的练习,常以板书示范,在教师眼中显而易见的计算环节对于很多学生并不能心领神会,要关注学生的状态与反应,及时沟通才能达到最佳教学效果.
3.4 督促学生正确、规范书写
对于高中生来说,好的书写就已经赢了第一步.事實上,良好的书写习惯不仅对于数学学科是有利的,对于其他科目一样是十分有帮助的.而在日常教学过程中,我们不难发现,很多学生粗心大意,将原本计算正确的题目由于书写潦草或者书写失误导致最终结果错误,例如,将2n+1写成2n+1,lg2·32写成lg2·32等等,由于这样的问题造成成绩不理想的结果实在是让人觉得可惜,而这是完全可以避免的.因此教师要多提醒学生,在平时的作业以及测试中将“好的书写”提上日程,并不断督促学生形成良好的书写习惯.
4 研究结论与不足
本文存在三点不足:(1)在此次调查中,只以一个学校作为调查样本,调查容量较小,而且参考的圆锥曲线题目样卷有限,具有一定的局限性;(2)本文没有对学生如何形成这些学习问题没有进行深入分析,论文探讨内容较浅;(3)由于时间以及本人的个人原因,使得此次调查的深度和广度不够,文中提到的建议与方法还需要进一步实践与探究.
参考文献:
[1]张鑫萌.基于ACT-R理论的圆锥曲线教学设计案例研究.2020,天津师范大学.
[2]何西.高中数学圆锥曲线学习障碍及应对策略.2018,四川师范大学.
[3]石伟娜.高二理科生运算能力的调查研究.2016,河北师范大学.

