时标上一些新的非线性Gronwall-Bellman积分不等式*
朱凡伟, 孟凡伟
(曲阜师范大学数学科学学院,273165,山东省曲阜市)
0 引 言
在20世纪80年代,Hilger创立了时标理论[1],以统一连续和离散分析. 此后越来越多的学者开始关注这一领域. 近年来,作为最基础的学科之一,时标上的动力学方程也得到了广泛的研究,并考虑了两个自变量的非线性不等式[2]. Gronwall-Bellman不等式[3,4]在许多应用中被用来研究不同动力学方程的解的有界性、全局存在性、稳定性等[5]. Pchpatte 不等式一直是一些研究人员讨论的主题[6-8]. 不等式被用作研究时标上动力学方程定性性质的重要工具[9-11].
本文给出了一些基于Gronwall-Bellman不等式的动态不等式,并利用基本动态不等式建立了大部分结果,其不仅推广了文献 [12] 中研究的一些动态不等式,还统一了一些连续时间和相应的离散时间的情况.
本文的结构如下:第1节介绍了时标上微积分的一些基本定义和引理[13,14];第2节在任意时间尺度上建立了一些新的 Gronwall-Bellman 不等式;第3节举例研究所得结果的应用.
1 预备知识
定义1假设是一个时标. 前跳算子σ:→定义为σ(t):=inf{s∈:s>t}, ∀t∈.后跳算子 ρ:→同样定义为 ρ(t):=sup{s∈:s 定义2 假设f:→是一个函数并且t∈k,将fΔ(t) 定义为一个数,只要它存在,其性质是:对任意ε>0,存在t的一个邻域U=(t-δ,t+δ),对任意δ>0,使得 |[f(σ(t))-f(s)]-fΔ(t)[σ(t)-s]|≤ε|σ(t)-s|s∈U, 称fΔ(t) 为f在t处的Delta或Hilger导数. 注1如果=,那么fΔ即为前向差 Δf(Δf(t)=f(t+1)-f(t)); 如果=,那么fΔ即为通常的导数f′. 定理1假设f,g:→且t∈k,下列结论成立: (ⅲ) 若f在t点是可微的,那么f(σ(t))=f(t)+μ(t)fΔ(t). (ⅳ) 若f和g在t点都可微,那么fg满足(fg)Δ(t)=fΔ(t)g(t)+f(σ(t))gΔ(t). 引理2[19]设u,v≥0 且p≥0,那么(u+v)p≤Kp(up+vp),其中Kp=1,0≤p≤1 或Kp=2p-1,p>1. 定义3R为所有回归函数和rd-连续函数的集合, R+={p∈R:1+μ(t)p(t)>0,t∈}. 引理3[20]若p∈R 且 t∈0,那么指数函数ep(t,t0) 是下列初值问题的唯一解, 引理4[15]假设y,f∈Crd(,) 且p∈R+. 若yΔ(t)≤p(t)y(t)+f(t),则 引理5[13](基本动态不等式) 设v(t) 是定义在k上的正函数,b(t) 和k(t) 是定义在k上的非负函数,并且b(t) 是回归函数,α>0 且α≠1 是一个常数. 若 vΔ(t)≤b(t)v(t)+k(t)vα(t) 对所有的t∈k成立且满足v1-α(t0)+(1-α)k(s)(e⊖b(σ(s),t0))1-αΔs>0,那么 对所有t∈k成立. 在本节中,为了便于阅读,假设t>t0,0=[t0,∞)∩k. 定理1 假设m,n,p,α,β,γ,q是非负常数且满足γ≥n>0,γ≥m>0,γ≥α>0,γ≥β>0,γ,p,q>0.v,a,f,g,k,b,c∈Crd(0,R+) ,ρ∈(0,0) 且ρ(t) (1) 其中t∈0. (ⅰ) 若 0 (2) 其中 (3) (4) (5) θ(t)=h1(t)+ρΔ(t)l1(ρ(t)). (6) (ⅱ)若 0 (7) 其中t2∈0满足条件 (8) 此外,若(8)式对所有t∈0成立,显然不等式 (7) 在t∈0上成立,其中 (9) (10) (11) (ⅲ) 若 1 (12) 其中t3∈0满足条件 (13) 此外,若(13)式对所有t∈0成立,显然不等式 (12) 在t∈0成立,其中 (14) (15) (16) 证明设 可以得出 vγ(t)≤a(t)+z(t). (17) 由于z(t) 是非负函数,通过(17)式和引理 1,得 (18) 情形1 若 0 (19) (20) 由(18),(19)和(20)式,可以得出 其中h1(t),l1(t) 和L1(t) 被定义为(3),(4)和(5)式.任取一点T∈0,当t∈[t0,T]∩时, 将上式的右半部分定义为u(t),可以看出来 z(t)≤u(t),u(t0)=L1(T), (21) 因此, uΔ(t)=h1(t)z(t)+ρΔ(t)l1(ρ(t))z(ρ(t)). 此外,对任意t∈[t0,T]∩,有ρ(t)∈[t0,T]∩,通过(21)式得z(ρ(t))≤u(ρ(t))≤u(t),那么 uΔ(t)≤h1(t)u(t)+ρΔ(t)l1(ρ(t))u(t)=[h1(t)+ρΔ(t)l1(ρ(t))]u(t)=θ(t)u(t). 由引理2.8有 u(t)≤L1(T)eθ(t,t0). (22) 设 (22)式中t=T,因为T是从0中任取的,接下来将T替换成t,由 (17) 和(21)式,得 情形2 若 0 (23) 由(18),(19)和(23)式,有 其中K1(t) 被定义为 (10)式. 任取一点T*∈0,当t∈[t0,T*]∩时, 将上述不等式的右半部分定义为χ1(t),可以看出来 z(t)≤χ1(t),χ1(t0)=K1(T*), (24) 因此 此外,对任意t∈[t0,t2]∩,有ρ(t)∈[t0,t2]∩. 由(24)式可得z(ρ(t))≤χ1(ρ(t))≤χ1(t),那么 其中A1(t),J1(t) 被定义为(9)和(11)式. 由引理 2.9得 (25) 设(25)式中t=T*,因为T*是从0中任选的,接下来将T*替换为t,由 (17)和(24)式,可得(7)式,其中 情形3 若 1 (26) 由(18),(20)和(26)式,可得 其中H1(t)被定义为(15)式,任取一点T◇∈0,当t∈[t0,T◇]∩时, 将上式的右半部分定义为G1(t),可以看出 z(t)≤G1(t),G(t0)=H1(T◇), (27) 因此 此外,对任意t∈[t0,t3]∩,有ρ(t)∈[t0,t3]∩,且由(27)式得z(ρ(t))≤G1(ρ(t))≤G1(t),那么 其中B1(t) 和Q1(t) 被定义为(14)式和(16)式.其余证明与情形2相同,此处省略. 这就完成了证明. 注1如果=,f(t)=g(t)=0,γ=1,定理1退化为文献[12]中的定理 2.1. 如果a(t)=c,g=f,γ=m=0,b(t)=0,γ=p=1,定理1退化为文献 [13] 中的定理 4.1. 定理2 假设m,n,p,q是非负常数且满足q≥n>0,q≥m>0,p>0.v,f,b,a,c∈Crd(0,+), 其中t∈0. (ⅰ) 若0 其中 满足所有的t∈0. (ⅱ) 若1 (28) 其中t1∈0满足条件 (29) 此外,若(29)式对所有t∈0成立,显然不等式 (28) 在t∈0上成立,其中 证明设 (30) 由于z(t) 是非负函数,得出vq(t)≤a(t)+z(t).由引理1,得 (31) 将(31)式代入(30)式中,得 接下来需要讨论p的范围,其余的证明与定理 2.1 中方法相同,此处省略. 这就完成了证明. 注2如果p=q=1,m=0,a(t)=c, 定理2退化为文献[13]中的定理 4.1. 如果=,f=0,p=n=1,a(t)=c, 定理2退化为文献[22]中的定理 2.3. 如果=,f=0,q=1, 定理 2 退化为文献 [18] 中的定理2.1. 给出上述结果的例子. 例1 某些非线性积分不等式在探索一些微分积分的定性性质方面发挥了作用. 考虑下列动态方程 (32) 满足条件vq(t0)=c,c是常数,其中v∈Crd(0,+),F∈Crd(0×+×+,+) 和G∈Crd(0×+,+) 是有界的,且满足 |F(t,M,N)|≤b(t)(|M|m+|N|)p,t∈0, (33) |G(t,W)|≤c(t)|W|n,0≤t<∞, (34) q≥n>0,q≥m>0,p>1.b,c∈Crd(0,+). 若∀t∈0, 并且 (35) (36) 证明对方程 (32) 两边从t0到t进行积分,得 再由(33)和(34)式可得 这是定理1的一种特殊形式 (当f=0,a(t)=c时),得到下列不等式 其中 上述不等式和假设(35)式,(36)式的逼近表明了(32)式的所有解在0上的有界性.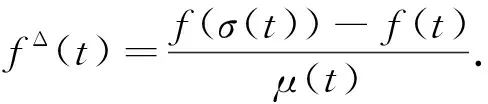
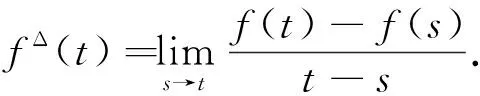

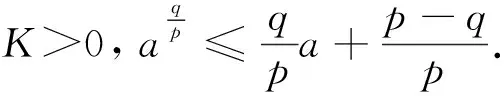

2 主要结果



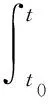



3 应 用

