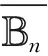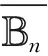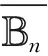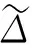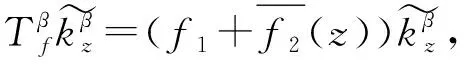Hardy-Sobolev空间上的投影Toeplitz算子*
林惠娜, 何 莉
(广州大学数学与信息科学学院,510006,广东省广州市)
0 引言及预备知识
对任意f∈H(n),定义H(n) 上f关于z的径向导数
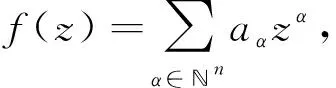
令dσ是n上的正规化面积测度,σ(n)=1. 令dv是n上的体积测度.对t>-1,令dvt(z)=ct(1-|z|2)tdv(z),其中ct是正规化的常数,使vt(n)=1. 当0 的全体可测函数所成空间.Lp(n,dvt)是由n上满足条件 的全体全纯函数所成空间. 对任意的ζ∈n,f∈H2,有进一步,f(ζ)∈L2(n,dσ),因此,H2上内积及其诱导范数分别为 对β∈,定义单位球上的 Hardy-Sobolev 空间 命题1[5]设β∈和f∈H(n),则下列条件等价: 进一步,如果N是大于β的非负整数,则上述条件还等价于 记 假设φ为n上二阶连续可微的函数,对一切1≤i,j≤n,若在n上满足则称φ为多重调和函数. 记多重调和 Hardy-Sobolev 空间是由Sobolev空间中所有的多重调和函数所成空间,则众所周知,n上的实值函数是多重调和的当且仅当该函数为n上全纯函数的实部. 因此,任意多重调和函数可唯一分解为其中对其中定义的范数为更多细节见文献 [10]. 从下文起,除非特别申明,将设β<0,且将对 Hardy-Sobolev 空间的研究转化为加权 Bergman 空间. 其中dv-2β-1(z)=c-2β-1(1-|z|2)-2β-1dv(z)为n上正规化的体积测度.令表示从到的正交投影. 设z=(z1,…,zn),w=(w1,…,wn) 是n中的任意两点,记则 其中函数Bf称为f的 Berezin 变换,详见文献 [11]. 命题4设f和g是n上的有界多重调和函数. 若f是共轭全纯函数且fg在n上是实值的,则在上, 由于g是n上的有界多重调和函数,因此存在全纯函数g1和g2,使得所以 又因为 结合以上两个结论,不难得到以下推论. 事实上,还可以得到以下结果. 证明若在n上,f≡0 a.e. 或者f≡1 a.e.,则是上的投影算子. 反之,若 Toeplitz 算子则在n上,f=1 a.e.. 若 Toeplitz 算子则存在非零函数为的核. 直接计算可知, 因此对z∈n,f(z)|h(z)|2=0 a.e..因为所以在n上,f=0 a.e.. 定理12设f和g是n上连续到边界的多重调和函数. 如果下列条件之一成立,则是投影算子. 定理13设f和g是n上有界多重调和函数. 如果下列条件之一成立,则是自伴算子. 证明若在n上,f是共轭全纯的且fg是实值函数,则 猜想14 设f和g是n上有界多重调和函数. 如果是自伴算子,则下列条件之一成立. 由文献[7]可知,猜想 14 对于n=1是成立的,尽管暂时无法完全证明这个猜想,仍可得到部分结果. 引理15设u是n上的二阶连续可微函数,u和属于L1(n,dvt), 则 同理可得 通过比较上面两个等式,可得 结合引理 15,并将不变 Laplace 算子作用于上式两边可得 由文献 [13] 可知, 是有界的. 因此 这说明对 ∀z,w∈n, 本文仅推导到这里,后续工作仍在考虑当中. (b) 对z∈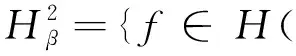
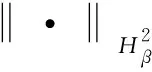
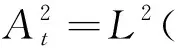
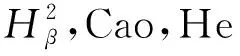

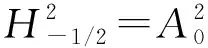

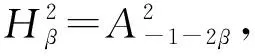


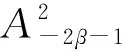
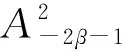


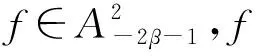
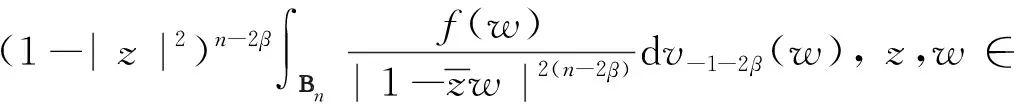



1 Hardy-Sobolev 空间上的 Toeplitz 算子
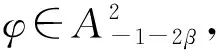




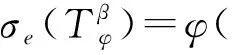

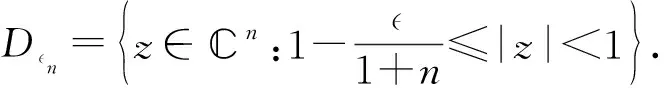
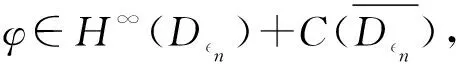



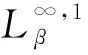

2 Hardy-Sobolev 空间上的算子乘积