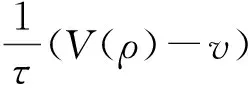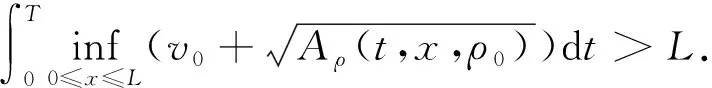非自治拟线性双曲组的节点状态精确边界能控性及渐近稳定性*
王利彬
(复旦大学数学科学学院,200433,上海市)
0 引 言
近年来,双曲型方程组的精确边界能控性问题被广泛关注和研究(见文献[1,2,5,6]等). 特别地,通过一个模块结构的构造性方法,对一维拟线性双曲型方程组
(0.1)
的局部精确边界能控性建立了完善的理论[6]. 概括起来,这个方法主要基于3个基本结论: 混合初边值问题半整体经典解的存在唯一性; 在没有零特征值的条件下,时间变量t和空间变量x的地位可交换; 单边混合初边值问题在最大决定区域内的经典解是唯一的.
2011年,从气体通过管道网输运以满足用户需求这一实际问题出发,Gugat等人提出了一类新的边界能控性问题. 与通常的精确边界能控性不同,这类能控性不是要求在边界控制的作用下混合初边值问题的解在某个适当大的时间T(>0)达到给定的终态,而是要求在边界控制的作用下解在某个适当大的时间T以后在一个或几个节点处满足给定的状态[4]. 同样利用一个基于上述3个基本结论的构造性方法,他们的这一结果很快被推广到具一般非线性边界条件的一阶拟线性双曲组(0.1)式,并称这类能控性为节点状态的精确边界能控性[7].
然而,在实际应用中,我们常会遇到非自治的拟线性双曲组,即(0.1)式中的A或F显含t的情形. 比如,交通流方程组[3,13]
我们将在第3节对它进行详细讨论.
对于非自治拟线性双曲组,是否也有与自治情形类似的精确边界能控性和节点状态精确边界能控性呢?前一问题已得到完满解决[12],对后一问题,若节点状态给在有限时间区间上时作者已于近期获得结果,但在无穷时间区间上,到目前为止,还没有相关结果. 本文将致力于解决这一问题,即:非自治一阶拟线性双曲组在无穷时间区间上的节点状态精确边界能控性及其渐近稳定性.
本文具体安排如下:在第1节,将给出节点状态精确边界能控性的定义和本文的主要结论;然后,在第2节给出主要结论的证明;最后,在第3节中将给出主要结论在交通流系统中的应用.
1 定义及主要结果
考虑如下的非自治一阶拟线性双曲组
(1.1)
其中t是时间变量,x是空间变量,u=(u1,…,un)T是(t,x)的未知向量函数,A(t,x,u)∈C1是给定的n×n矩阵函数,F(t,x,u)是给定的C1模有界的n维向量值函数,且满足
F(t,x,0)=0.
(1.2)
由(1.2)式知,u=0是(1.1)式的一个平衡态.
由双曲性,矩阵A(t,x,u)在所考察的区域上有n个实的特征值λr(t,x,u)及一组完备的左(相应地,右)特征向量li(t,x,u)=(li1(t,x,u),…,lin(t,x,u))(相应地ri(t,x,u)=(r1i(t,x,u),…,rni(t,x,u))T)(i=1,2,…,n),即
li(t,x,u)A(t,x,u)=λi(t,x,u)li(t,x,u)(相应地A(t,x,u)ri(t,x,u)=λi(t,x,u)ri(t,x,u)),
(1.3)
det|lij(t,x,u)|≠0(相应地det|rji(t,x,u)|≠0).
(1.4)
不失一般性,假设在所考察的区域上有
li(t,x,u)rj(t,x,u)≡δij(i,j=1,2,…,n),
(1.5)
(1.6)
其中δij表示Kronecker符号.
假设λi,li和ri(i=1,2,…,n)均为C1模有界的函数且在所考察的区域上双曲组(1.1)没有零特征值,即
λr(t,x,u)<0<λs(t,x,u)(r=1,2,…,m;s=m+1,…,n),
(1.7)
其中1≤m vi=li(t,x,u)u(i=1,2,…,n) (1.8) 为方程组(1.1)的对角化变量. 注意到(1.7),对于方程组(1.1)的前向混合初边值问题,我们给如下的初始条件 t=0:u=φ(x),0≤x≤L (1.9) 和边界条件 x=0:vs=Gs(αs(t),v1,…,vm)+Hs(t)(s=m+1,…,n), (1.10) x=L:vr=Gr(αr(t),vm+1,…,vn)+Hr(t)(r=1,2,…,m), (1.11) 其中φ,Gi,αi(t)和Hi(i=1,2,…,n)均为C1函数,并且αi(t)(i=1,2,…,n)可为向量值函数. 不失一般性,假设Gi满足 Gi(αi(t),0,…,0)≡0(i=1,2,…,n). (1.12) (1.13) 然后, (1.14) 要实现节点状态的精确边界能控性,仅需要求初值,给定的节点状态和已知的边界函数具有适当小的C1模. 具体地说,有以下定理. 定理1 令T满足 (1.15) 这个定理的证明将在2.1节中给出. 下面考察能控性的渐近稳定性. 与自治情形类似[11],假设节点状态和已知的边界函数具有指数或多项式衰减性,那么可以得到边界控制函数和相应的混合初边值问题的解也具有同样的衰减性. (1.16) (1.17) 其中a是正常数,则一定存在边界控制Hs(t)(s=m+1,…,n),满足 eat(|Hs(t)|+|h′s(t)|)≪1(s=m+1,…,n),∀t≥0, (1.18) 使得混合初边值问题(1.1)及(1.9)~(1.11)在区域R={(t,x)|0≤t<+∞,0≤x≤L}上存在唯一的C1解u=u(t,x),满足 eat(|u(t,x)|+|ut(t,x)|)≪1,∀t≥0,0≤x≤L, (1.19) (1.20) (1.21) 其中μ是正常数,则一定存在边界控制Hs(t)(s=m+1,…,n),满足 (1+t)μ(|Hs(t)|+|h′s(t)|)≪1(s=m+1,…,n),∀t≥0, 使得混合初边值问题(1.1)及(1.9)~(1.11)在区域R={(t,x)|0≤t<+∞,0≤x≤L}上存在唯一的C1解u=u(t,x),满足 (1+t)μ(|u(t,x)|+|ut(t,x)|)≪1,∀t≥0,0≤x≤L, 定理2和定理3的证明将分别在2.2节和2.3节中给出. 注2 对于方程组(1.1),如果初始条件(1.9)被取在t=T0时刻,其中T0是一个任意给定的正数,那么条件(1.15)应被 替代,此时,定理1、定理2和定理3中的相应结论依然成立. 这意味着控制时间T虽然依赖于T0,但系统的节点状态精确边界能控性总能实现. 这一性质与非自治双曲组的精确边界能控性明显不同[9]. 注3 对于节点x=0,可以类似地定义和讨论其节点状态精确边界能控性,此时,节点状态给在x=0上,边界控制取为Hr(t)(r=1,2,…,m),而(1.15)应被替代为 在这一节,将用引言中提到的构造性方法来证明本文的主要定理. 首先,由(1.7)和(1.15)式知, 存在适当小的ε0>0和T1∈(0,T),使得 (2.1) 在区域R(T1)={(t,x)|0≤t≤T1,0≤x≤L}上,考虑方程组(1.1)具初始条件(1.9)、边界条件(1.11)及如下人工边界条件 x=0:vs=gs(t)(s=m+1,…,n) (2.2) 的前向混合初边值问题,其中gs(t)是任意给定的C1[0,T1]模适当小的C1函数,且在点(t,x)=(0,0)处满足C1相容性条件. 由非自治拟线性双曲组半整体C1解理论[12]可知,此前向混合初边值问题在区域R(T1)上存在唯一的C1解u=uf(t,x),其C1模充分小. 特别有 |uf(t,x)|≤ε0,∀(t,x)∈R(T1). (2.3) 由T1 (2.4) 由于方程组(1.1)没有零特征值,交换t和x的地位得到 (2.5) 对方程组(2.5),考虑半无界区域R={(t,x)|0≤t<+∞,0≤x≤L}上的左向混合初边值问题,其边界条件由原初始条件(1.9)导出 t=0:vr=vr(x)≜lr(0,x,φ(x))φ(x)(r=1,2,…,m),0≤x≤L, (2.6) 初始条件为 x=L:u=u(t),t≥0, (2.7) 其中u(t)由隐式关系 (2.8) 确定,这里vs(t)(s=m+1,…,n)已知,vr(t)(r=1,2,…,m)由边界条件(1.11)给出,即 vr(t)=Gr(αr(t),vm+1(t),…,vn(t))+Hr(t)(r=1,2,…,m), (2.9) 从而u(t)满足边界条件(1.11). 注意到(1.12)式,由(1.11)式有 (2.10) (2.11) 其中θ∈(0,1). 然后,注意到(1.6)式,Hr(t)和αr(t)(r=1,2,…,m),以及vs(t)(s=m+1,…,n) 具有适当小的C1模,从(2.8)式可以得到u(t)在区间[0,+∞)上满足 (2.12) 于是,用类似于文献[11]中定理3.1的证明方法可以获得: 这个左向问题存在唯一的C1解u=u(t,x),其C1模充分小,特别有 |u(t,x)|+|ut(t,x)|≤ε0,∀t≥0,0≤x≤L. (2.13) 显然,u=u(t,x)满足方程组(1.1)及边界条件(1.11),下面验证其还满足初始条件(1.9). 事实上,u=u(t,x)和u=uf(t,x)均为单边混合初边值问题(2.5)、(2.6)及 (2.14) 在最大决定区域Ω上的C1解. 由唯一性有 u(t,x)≡uf(t,x),∀(t,x)∈Ω. (2.15) 注意到(2.3)和(2.13)式,由T1的选取(2.1)式易知,Ω包含初始轴t=0上的区间[0,L],从而u=u(t,x)满足初始条件(1.9). 最后,把u=u(t,x)代入到边界条件(1.10)中,即得到在整个时间区间t≥0上的边界控制函数Hs(t)(s=m+1,…,n),并且由(1.12)和(2.13)式可知‖Hs‖C1[0,+∞)充分小. 定理2的证明过程与定理1的证明类似,我们仅仅指出本质不同之处. 注意到(1.16)~(1.17),代替(2.12),从(2.8)可以得到 (2.16) 于是,用类似于文献[11]中定理3.3的证明方法可以获得: 这个左向问题存在唯一的C1解u=u(t,x),且满足 eat(|u(t,x)|+|ut(t,x)|)≪1,∀t≥0,0≤x≤L. (2.17) 最后,把u=u(t,x)代入到边界条件(1.10)中,即得到在整个时间区间t≥0上相应的边界控制函数Hs(t)(s=m+1,…,n),并且由(1.12)和(2.17)可知(1.18)成立. 定理3的证明与定理1和定理2的证明类似,注意到(1.20)~(1.21)式,仅需将(2.16)式中的权eat换成(1+t)μ,并利用类似于文献[11]中定理3.5的证明方法即可获得我们需要的结论,至于细节不再赘述. 本节考虑交通流方程组 (3.1) A(t,x,ρ0)≡0, (3.2) Aρ(t,x,ρ0)>V2(ρ0), (3.3) 其中ρ0为正常数. 记V(ρ0)为v0,由(3.2)式知,(ρ0,v0)为(3.1)式的一个平衡态. 由(3.3)式知,在(ρ,v)=(ρ0,v0)的一个邻域,方程组(3.1)是严格双曲的,其特征值为 相应的左特征向量可取为 (3.4) 考虑方程组(3.1)具如下初始条件 和速度边界条件 x=0:v=v0+h2(t), (3.5) x=L:v=v0+h1(t) (3.6) 从而得到 显然,(ρ,v)=(ρ0,v0)等价于(V1,V2)=(0,0),并且可将(3.5)~(3.6)改写为 x=0:V2=-V1+2h2(t),x=L:V1=-V2+2h1(t). 其中a和μ为正常数,则相应地由定理1~定理3之一可得该交通流系统在节点x=L上有节点状态精确边界能控性和相应的渐近稳定性,h2(t)为控制函数. 对节点x=0可进行相应的讨论. 此外,若速度边界条件(3.5)~(3.6)换成密度边界条件 x=0:ρ=ρ0+H2(t),x=L:ρ=ρ0+H1(t), 或流量边界条件 x=0:ρv=ρ0v0+H2(t),x=L:ρv=ρ0v0+H1(t), 在适当的条件下,也可到相应的结果.
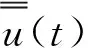
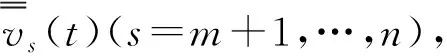

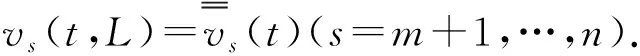

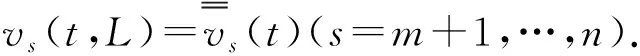
2 主要定理的证明
2.1 定理1的证明


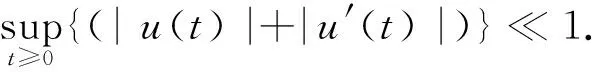
2.2 定理2的证明
2.3 定理3的证明
3 应 用