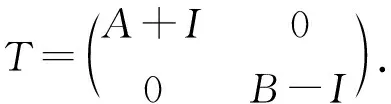算子及其函数的(UWπ)性质与(ω)性质*

车雨红, 戴 磊, 郭志华

(①渭南师范学院数学与统计学院,714099,渭南市; ②陕西师范大学数学与统计学院,710119,陕西省西安市)

0 引言及预备知识

在本文中,H表示无限维复可分的Hilbert空间,B(H)为H上的有界线性算子的全体. 对T∈B(H),用N(T)和R(T)表示T的零空间和值域. 根据T的零空间N(T)的维数n(T)与R(T)的余维数d(T)的有限性可以定义半Fredholm算子:若n(T)<∞且R(T)为闭集,称T为上半Fredholm算子. 若T为上半Fredholm算子且n(T)=0,称T为下有界算子. 若d(T)<∞,称T为下半Fredholm算子. 若n(T)<∞且d(T)<∞,则称T为Fredholm算子. 当算子T为半Fredholm算子时(上半Fredholm算子或者下半Fredholm算子),其指标定义为ind(T)=n(T)-d(T). 若ind(T)=0,称T为Weyl算子. 算子T的升标asc(T)为满足N(Tn)=N(Tn+1)的最小的非负整数,若这样的整数不存在,记asc(T)=+∞;算子T的降标des(T),为满足R(Tn)=R(Tn+1)的最小的非负整数,同样当这样的整数不存在时,记des(T)=+∞. 若asc(T)<∞且des(T)<∞,可以证明asc(T)=des(T). 若算子T有有限的升降标,称T为Drazin可逆算子. 算子T称为是Browder算子,若T为具有有限升标和有限降标的Fredholm算子. 可以证明T为Browder算子当且仅当T为半Fredholm 算子且当0<|λ|充分小时,T-λI可逆. 用σ(T)表示算子T∈B(H)的谱集. 通过上述叙述,可以定义算子T的上半Fredholm谱σSF+(T)、逼近点谱σa(T)、Drazin谱σD(T)以及Browder谱σb(T)为

可以看出算子值域的闭性以及算子的Kato性质在算子理论中是重要的. 设ρk(T)={λ∈:其余集σk(T)=ρk(T)称为算子T的Kato谱. 记σc(T)={λ∈:R(T-λI)不闭}. 另外,记σ0(T)为算子T的所有正规特征值组成的集合,即σ0(T)=σ(T)σb(T).若集合E为复数集的子集,则分别用isoE、accE和∂E表示集合E的孤立点的全体、聚点的全体以及边界点的全体.

1909年,Weyl H[1]发现Hilbert空间中自伴算子的Weyl谱恰好等于该算子的谱集除去有限重的孤立特征值,这个结论被称作Weyl定理. 之后,许多数学工作者将Weyl定理进行了变型和推广,定义了(ω)性质以及(UWπ)性质等[2-4]. (UWπ)性质和(ω)性质是Weyl定理的新的变型,近年来备受关注[5-7]. 在本文中,讨论了有界线性算子的(UWπ)性质和(ω)性质之间的关系,给出了有界线性算子同时满足(UWπ)性质和(ω)性质的条件,并且讨论了算子函数同时满足(UWπ)性质和(ω)性质的条件.

1 有界线性算子的(UWπ)性质和(ω)性质

首先给出(UWπ)性质[4]和(w)性质[2]的定义.

对T∈B(H),若σa(T)σea(T)=PD(T),则称T满足(UWπ)性质,其中PD(T)=σ(T)σD(T)={λ∈σ(T):T-λI是Drazin可逆算子};若σa(T)σea(T)=π00(T),称T满足(ω)性质,其中π00(T)={λ∈isoσ(T):0

首先通过举例,讨论一下(UWπ)性质和(ω)性质之间的关系.

注解1.1(1) 算子具有(ω)性质,并不能推出其具有(UWπ)性质.

例如，设T∈B(l2)定义为T(x1,x2,x3,…)=(0,x2,x3,…).经计算得σa(T)={0,1},σea(T)={1},π00(T)={0},PD(T)={0,1},则T具有(ω)性质,但不具有(UWπ)性质.

(2) 算子具有(UWπ)性质并不能推出其具有(ω)性质.

(3) 存在算子既不具有(UWπ)性质,又不具有(ω)性质.

例如，设A,B∈B(l2)定义为

A(x1,x2,x3,…)=(0,x1,x2,…);B(x1,x2,x3,…)=(0,x2,x3,…),

(4) 当算子T既具有(UWπ)性质,又具有(ω)性质时,一定有π00(T)=PD(T)=σ0(T).

由注解1.1可以看出,虽然(UWπ)性质和(ω)性质从形式上来看具有关联,但是它们之间并没有必然的联系. 下面讨论算子T同时满足(UWπ)性质和(ω)性质的充要条件.

定理1.1设T∈B(H),则下列叙述等价：

(1)T同时具有(UWπ)性质和(ω)性质;

(2)σb(T)=[σea(T)∩accσ(T)]∪{λ∈σ(T):n(T-λI)=0}∪{λ∈σD(T):n(T-λI)=∞};

(3)σb(T)=σD(T)=[σea(T)∪accσ(T)]∪{λ∈σ(T):n(T-λI)=0}∪{λ∈:n(T-λI)=∞}.

证明下证(1)和(2)等价. 设σb(T)=[σea(T)∩accσ(T)]∪{λ∈σ(T):n(T-λI)=0}∪{λ∈σD(T):n(T-λI)=∞}. 由于 [σa(T)σea(T)]∩[σea(T)∩accσ(T)]=∅,[σa(T)σea(T)]∩{λ∈σ(T):n(T-λI)=0}=∅,且[σa(T)σea(T)]∩{λ∈σD(T):n(T-λI)=∞}=∅,故[σa(T)σea(T)]∩σb(T)=∅,从而σa(T)σea(T)⊆σ0(T)⊆π00(T)且σa(T)σea(T)⊆σ0(T)⊆PD(T).

又[PD(T)∪π00(T)]∩{[σea(T)∩accσ(T)]∪{λ∈σ(T):n(T-λI)=0}∩{λ∈σD(T):n(T-λI)=∝}}=∅,故[PD(T)∪π00(T)]∩σb(T)=∅,从而 [PD(T)∪π00(T)]⊆σ0(T)⊆σa(T)σea(T).因此,T同时具有(UWπ)性质和(ω)性质.

反之,设(1)成立,即T同时具有(UWπ)性质和(ω)性质. 包含关系σb(T)⊇[σea(T)∩accσ(T)]∪{λ∈σ(T):n(T-λI)=0}∪{λ∈σD(T):n(T-λI)=∞}显然成立. 反之,∀λ0∉[σea(T)∩accσ(T)]∪{λ∈σ(T):n(T-λI)=0}∪{λ∈σD(T):n(T-λI)=∞}.不妨设λ0∈σ(T),则n(T-λ0I)>0,即λ0∈σa(T).

断言:λ0∈PD(T).

事实上,若不然,设λ0∉PD(T),即λ0∈σD(T). 由λ0∉{λ∈σD(T):n(T-λI)=∞}知n(T-λ0I)<∞.

若λ0∉σea(T),则λ0∈σa(T)σea(T). 由于T满足(UWπ)性质,于是λ0∈PD(T),矛盾.

若λ0∉accσ(T),即λ0∈isoσ(T). 此时可看出λ0∈π00(T). 由T具有(w)性质可知λ0∈σ0(T)⊆PD(T). 再次得到矛盾.

于是断言成立,即λ0∈PD(T). 由于T满足(UWπ)性质知λ0∈σ0(T),于是λ0∉σb(T).

(1)和(3)等价可类似得证.

对T∈B(H),若isoσ(T)⊆σp(T),则称T为isoloid算子,其中σp(T)表示算子T的特征值.

再结合定理1.1可得下列推论.

推论1.1设T∈B(H),则下列叙述等价:

(1)T为isoloid算子且T同时具有(UWπ)性质和(ω)性质;

(2)σb(T)=[σea(T)∩accσ(T)]∪[ρa(T)∩σ(T)]∪{λ∈σD(T):n(T-λI)=∞};

(3)σb(T)=σD(T)=[σea(T)∩accσ(T)]∪[ρa(T)∩σ(T)]∪{λ∈σD(T):n(T-λI)=∞}.

在(UWπ)性质和(ω)性质中,[σa(T)σea(T)∪PD(T)∪π00(T)]∩[accσea(T)∪accσk(T)]=∅.下面利用accσea(T)∪accσk(T)刻画(ω)性质和(UWπ)性质.

推论1.2设算子T∈B(H),则下列叙述等价:

(1)T同时具有(UWπ)性质和(ω)性质;

(2)σb(T)=accσea(T)∪accσk(T)∪{λ∈σ(T):n(T-λI)=0}∪[acc {λ∈:n(T-λI)

(3)σb(T)=σD(T)=accσea(T)∪accσk(T)∪{λ∈σ(T):n(T-λI)=0}∪[acc {λ∈:n(T-λI)

(4)σb(T)=accσea(T)∪acc isoσ(T)∪{λ∈σ(T):n(T-λI)=0}∪[acc {λ∈:n(T-λI)

(5)σb(T)=σD(T)=accσea(T)∪acc isoσ(T)∪{λ∈σ(T):n(T-λI)=0}∪[acc {λ∈:n(T-λI)

证明(1)⟹(2). 只需证σb(T)⊆accσea(T)∪accσk(T)∪{λ∈σ(T):n(T-λI)=0}∪[acc {λ∈:n(T-λI)

对任意的λ0∉accσea(T)∪accσk(T)∪{λ∈σ(T):n(T-λI)=0}∪[acc {λ∈:n(T-λI)0,于是λ0∈σa(T). 由λ0∉accσea(T)∪accσk(T)知,∃>0使得当0<|λ-λ0|<时,其中是上半Fredholm算子且ind(T)≤0},并且若存在λ1满足0<|λ1-λ0|<使得λ1∈σa(T),则λ1∈σa(T)σea(T)=π00(T),即λ1∈σ0(T),于是N(T-λ1I)=N(T-λ1I)∩R[(T-λ1I)k]={0},其中k为T-σ1I的升标,从而T-σ1I可逆,得到矛盾. 于是λ0∈isoσa(T).

断言:λ0∉σD(T).

事实上,若λ0∈σD(T),由λ0∈isoσa(T)以及λ0∉{λ∈isoσa(T)∩σD(T):n(T-λI)=∞}知0

情形1 设λ0∉acc {λ∈:n(T-λI)

根据λ0∈isoσa(T),此时λ0∈isoσ(T),于是λ0∈π00(T). 由T具有(ω)性质知λ0∈σ0(T),这与λ0∈σD(T)矛盾.

情形2 设λ0∉σc(T).

此时T-λ0I是上半Fredholm算子,且n(T-λ0I)>0. 由λ0∈isoσa(T)知λ0∈σa(T)σea(T). 由算子T具有(ω)性质知,λ0∉σD(T),再次矛盾. 于是断言λ0∉σD(T)成立,即λ0∈PD(T). 由算子T具有(UWπ)性质知λ0∉σb(T).

(2)⟹(1). 由条件知,

accσea(T)∪accσk(T)⊆σea(T)∩accσ(T),

acc {λ∈:n(T-λI)

{λ∈isoσa(T)∩σD(T):n(T-λI)=∞}∪{λ∈σD(T):n(T-λI)=∞}.

从而σb(T)⊆[σea(T)∩accσ(T)]∪{λ∈σ(T):n(T-λI)=0}∪{λ∈σD(T):(T-λI)=∞}.

所以σb(T)=σea(T)∩accσ(T)]∪{λ∈σ(T):n(T-λI)=0}∪{λ∈σD(T):n(T-λI)=∞},由定理1.1可知T同时具有(UWπ)性质和(ω)性质.

同理可证(1)和(3)的等价性,(1)和(4)的等价性以及(1)和(5)的等价性.

注解1.2在推论1.2中,当算子T同时具有(UWπ)性质和(ω)性质时,σb(T)分解的5部分缺一不可.

例1设T∈B(l2)定义为T(x1,x2,x3,…)=(x2,x3,x4,…). 经计算得

(1)σa(T)=σea(T)={λ∈:|λ|≤1},π00(T)=PD(T)=∅,则算子T同时具有(UWπ)性质和(ω)性质;

(2) accσk(T)∪{λ∈σ(T):n(T-λI)=0}∪[acc {λ∈:n(T-λI)

从而accσea(T)不能缺失.

例3设T∈B(l2)定义为T(x1,x2,x3,…)=(0,x1,x2,x3,…). 经计算得σb(T)≠accσea(T)∪accσk(T)∪[acc {λ∈:n(T-λI)

同理可证得下列结论.

推论1.3 设算子T∈B(H),则下列叙述等价:

(1)T为isoloid算子且具有(UWπ)性质和(ω)性质;

(2)σb(T)=accσea(T)∪accσk(T)∪[ρa(T)∩σ(T)]∪[acc {λ∈:n(T-λI)

(3)σb(T)=accσea(T)∪acc isoσ(T)∪[ρa(T)∩σ(T)]∪[acc {λ∈:n(T-λI)

(4)σb(T)=σD(T)=accσea(T)∪acc isoσ(T)∪[ρa(T)∩σ(T)]∪[acc {λ∈:n(T-λI)

由升降标及谱集之间的关系知，当λ0∈∂σ(T)且des(T-λ0I)<∞时,λ0∈PD(T)[8,定理2.1〗. 下面继续讨论,算子T具有(UWπ)性质和(ω)性质的判定条件. 令ρdes(T)={λ∈:des(T-λI)<∞},σdes(T)=ρdes(T). 由文献[8]中引理2.4知,ρdes(T)⊆为开集,从而σdes(T)为闭集.

在上面的定理及推论中,将“{λ∈isoσa(T)∩σD(T):n(T-λI)=∞}”或者“{λ∈σD(T):n(T-λI)=∞}”改为“{λ∈σdes(T):n(T-λI)=∞}”,结论仍然成立.

推论1.4设T∈B(H),则

(1)T同时具有(UWπ)性质和(ω)性质当且仅当σb(T)=accσ(T)∪{λ∈σdes(T):n(T-λI)=∞}=σea(T)∪{λ∈σ(T):n(T-λI)=0}.

(2)T为isoloid的且同时具有(UWπ)性质和(ω)性质当且仅当σb(T)=accσ(T)∪{λ∈σdes(T):n(T-λI)=∞}=σea(T)∪[ρa(T)∩σ(T)].

2 算子函数的(UWπ)性质和(ω)性质

当算子T同时具有(UWπ)性质和(ω)性质时,并不能推出其算子函数同时具有(UWπ)性质和(ω)性质. 例如:设A,B∈B(l2)定义为

A(x1,x2,x3,…)=(0,x1,x2,…);B(x1,x2,x3,…)=(x2,x3,…),

下面讨论算子函数同时具有(UWπ)性质和(ω)性质的条件. 需要下列事实[9,定理2.2〗:对任意的多项式p,p(σea(T))=σea(p(T))当且仅当∀λ,μ∈ρSF+(T),都有ind(T-λI)·ind(T-μI)≥0.

定理2.1设T∈B(H),则对任意的多项式p,p(T)同时具有(UWπ)性质和(ω)性质当且仅当

(1)T同时具有(UWπ)性质和(ω)性质;

(2) ∀λ,μ∈ρSF+(T),ind(T-λI)·ind(T-μI)≥0;

(3) 若σ0(T)≠∅,则σb(T)=[σea(T)∩accσ(T)]∪{λ∈:n(T-λI)=∞}.

证明必要性.

(1) 显然成立.

(2) 若存在λ0,μ0∈ρSF+(T),使得ind(T-λ0I)>0,ind(T-μ0I)<0. 显然T-λ0I为Fredholm算子. 设ind(T-λ0I)=n>0,ind(T-μ0I)=-m<0,其中m为正整数或者+∞. 若m为正整数,设p(x)=(x-λ0)m(x-μ0)n. 则p(T)为Weyl算子且n(p(T))>0,即0∈σa(p(T))σea(p(T)). 由于p(T)满足(ω)性质,于是p(T)为Browder算子,从而T-λ0I为Browder算子,即ind(T-λ0I)=0,这就与ind(T-λ0I)=n>0矛盾;若m=+∞,设p(x)=(x-λ0)(x-μ0),同样可知0∈σa(p(T))σea(p(T)). 类似于上面证明,再次得到矛盾.

(3) 若σ0(T)≠∅,此时一定有σa(T)=σ(T). 事实上,取λ1∈σ0(T). 设T-λ2I下有界,令p(T)=(T-λ1I)(T-λ2I),则0∈σa(p(T))σea(p(T)). 由p(T)满足(ω)性质知p(T)为Browder算子,从而T-λ2I为Browder算子. 结合T-λ2I为下有界算子,于是T-λ2I可逆. 所以σa(T)=σ(T).

任给λ0∉[σea(T)∩accσ(T)]∪{λ∈:n(T-λI)=∞},则n(T-λ0I)<∞. 若λ0∉σea(T),则λ0∈ρa(T)∪[σa(T)σea(T)],于是λ0∈[ρ(T)∪σ0(T)],从而λ0∉σb(T). 若λ0∉accσ(T),不妨设λ0∈isoσ(T). 选取λ1∈σ0(T). 令σ1={λ0},σ2={λ1},σ3=σ(T)[σ1∪σ2]. 由文献[10]中定理2.10可知,T可分解为

其中σ(Ti)=σi. 令F0(z)=(z-λ0)(z-λ1),则

同时σ(F0(T1))=σ(F0(T2))={0}且0∉σ(F0(T3))，于是0∈isoσ(F0(T)). 又由于0

这样就有σb(T)=[σea(T)∩accσ(T)]∪{λ∈:n(T-λI)=∞}.

对充分性,分两种情况讨论.

情况1 设σ0(T)=∅. 由T满足(UWπ)性质和(ω)性质可知σa(T)=σea(T)且π00(T)=PD(T)=∅.σa(·)满足谱映射定理,由条件(2) 知σea(·)也满足谱映射定理,于是对任意的多项式p,σa(p(T))=p(σa(T))=p(σea(T))=σea(p(T)). 又由于π00(p(T))⊆p(π00(T))以及PD(p(T))⊆p(PD(T))知π00(p(T))=PD(p(T))=∅. 由此可看出对任意的多项式p,p(T)同时具有(UWπ)性质和(ω)性质.

情况2 设σ0(T)≠∅. 由条件(3)知σb(T)=σea(T),且T为isoloid算子. 对任意多项式p,设μ0∈π00(p(T)),并且设p(T)-μ0I=a(T-λ1I)n1(T-λ2I)n2…(T-λkI)nk,其中λi≠λj(i≠j). 不妨设λi∈σ(T). 由于T为isoloid算子且n(T-λiI)≤n(p(T)-μ0I)<∞知λi∈π00(T). 由T满足(ω)性质知T-λiI为Browder算子,于是p(T)-μ0I为Browder算子,即π00(p(T))⊆σa(p(T))σea(p(T)). 反之,设μ0∈σa(p(T))σea(p(T))，且令

p(T)-μ0I=a(T-λ1I)n1(T-λ2I)n2…(T-λkI)nk,

其中λi≠λj(i≠j). 由条件(2)知ind(T-λiI)≤0,于是对每一个i,都有λi∉σea(T). 由σea(T)=σb(T)知T-λiI为Browder 算子. 所以p(T)-μ0I为Browder算子,即λ0∈π00(p(T)). 因此p(T)满足(ω)性质.

对(UWπ)性质,由上面的证明过程可知,对于任意的多项式p,都有σa(p(T))σea(p(T))⊆π00(p(T)),则σa(p(T))σea(p(T))⊆PD(p(T)). 任给μ0∈PD(p(T)),仍然设p(T)-μ0I=a(T-λ1I)n1(T-λ2I)n2…(T-λkI)nk,其中λi≠λj(i≠j). 不妨设λi∈σ(T),又由于σD(·)满足谱映射定理,于是λi∉σD(T). 结合T满足(UWπ)性质,T-λiI为Browder算子,因而p(T)-μ0I为Browder 算子. 因此μ0∈σa(p(T))σea(p(T)). 于是p(T)满足(UWπ)性质.

在定理2.1中,将条件(3)改为“若σ0(T)≠∅,则σb(T)=accσea(T)∪accσk(T)∪{λ∈:n(T-λI)=∞}”或者“若σ0(T)≠∅,则σb(T)=accσea(T)∪acc isoσ(T)∪{λ∈:n(T-λI)=∞}”,或“若λ0(T)≠∅,则σb(T)=accσa(T)∪{λ∈σdes(T):n(T-λI)=∞}”,结论仍成立.

若σb(T)=[σea(T)∩accσ(T)]∪{λ∈:n(T-λI)=∞},则任给λ∈ρSF+(T),都有ind(T-λI)≥0. 于是有下面的推论2.1.

推论2.1设算子T∈B(H),则对任意的多项式p,p(T)具有(UWπ)性质和(ω)性质当且仅当算子T同时具有(UWπ)性质和(ω)性质,且下列之一成立：

(1)σb(T)=[σea(T)∩accσ(T)]∪{λ∈:n(T-λI)=∞};

(2)σa(T)=σea(T),且∀λ,μ∈ρSF+(T),都满足ind(T-λI)·ind(T-μI)≥0.

证明必要性. 若σ0(T)=∅,由定理2.1知(2)成立. 而当σ0(T)≠∅,由定理2.1知(1)成立.

充分性. 若(1)成立,则定理2.1中的条件(1)～(3)均满足,故由定理2.1知对任意的多项式p,p(T)具有(UWπ)性质和(ω)性质.

若(2)成立,由于T满足(UWπ)性质和(ω)性质,于是σ0(T)=∅.再次由定理2.1知对任意的多项式p,p(T)具有(UWπ)性质和(ω)性质.

若对任意的多项式p,p(T)均满足(ω)性质,可证得定理2.1中的(2)和(3)均成立. 又由于σD(·)满足谱映射定理,可知下列结论:设T∈B(H)具有(UWπ)性质. 若对任意的多项式p,p(T)均满足(ω)性质,则对任意的多项式p,p(T)均满足(UWπ)性质.

例2.1设T∈B(l2)定义为T(x1,x2,x3,…)=(0,x1,x2,x3,…),则T满足定理2.1中的条件(1)～(3)，于是对任意的多项式p,p(T)具有(UWπ)性质和(ω)性质.