Weyl定理及其紧摄动*
杨莉莉, 曹小红
(陕西师范大学数学与统计学院,710119,陕西省西安市)
0 引 言
在本文中,H表示无限维可分的复Hilbert空间,B(H)和K(H)分别表示H上的全体有界线性算子和全体紧算子构成的集合. 对T∈B(H),用n(T)和d(T)分别表示算子T的零空间N(T)的维数和值域R(T)的余维数,即n(T)=dimN(T),d(T)=dim[HR(T)]=codimR(T). 算子T的升标和降标分别定义为
asc(T)=inf{n∈:N(Tn)=N(Tn+1)},
des(T)=inf{n∈:R(Tn)=R(Tn+1)},
对于T∈B(H),T的谱集定义为
σ(T)={λ∈:T-λI不为可逆算子}.
T的Weyl谱σw(T),Browder谱σb(T),半Fredholm谱σSF(T)分别定义为
σw(T)={λ∈:T-λI不为Weyl算子};
σb(T)={λ∈:T-λI不为Browder算子};
σSF(T)={λ∈:T-λI不为半Fredholm算子}.
显然,σSF(T)⊆σw(T)⊆σb(T).
令ρ(T)=σ(T),ρw(T)=σw(T),ρSF(T)=σSF(T).σ0(T)表示T的所有正规特征值构成的集合,即σ0(T)=σ(T)σb(T).
设T∈B(H),称T满足Browder定理,如果
σ(T)σw(T)⊆π00(T),
其中,π00(T)={λ∈isoσ(T):0 若σ(T)σw(T)=π00(T),则称T满足Weyl定理. 显然,Weyl定理⟹Browder定理. 若对任意K∈K(H),T+K都满足Weyl定理,则称T具有Weyl定理稳定性. 1909年,Weyl[1]在检查Hermitian算子T的谱结构时发现,T的所有紧扰动谱集的交集在其谱集中的余集恰好等于它的谱集中孤立点的有限重特征值. 这一性质后来被称为“Weyl定理”. 之后,许多学者对算子的Weyl定理及其稳定性作了大量的研究工作(见文献[2-6]). 本文对B(H)中一类具有特殊谱结构的算子的Weyl定理及其紧扰动进行讨论,并且将文献[2]中有关复对称算子Weyl定理的研究结果进行了拓展. 引理1.1[7]设T∈B(H). 若λ∈isoσ(T),则下列等价: (1)λ∈ρSF(T); (2)λ∈ρw(T); (3)λ∈σ0(T). 引理1.2[8]设T∈B(H). 若σ(T)=σSF(T)∪σ0(T),则对任意的>0,都存在K∈K(H)满足‖K‖<,σ(T+K)=σSF(T+K)∪σ0(T+K)且isoσ(T+K)=σ0(T+K). 由引理1.2我们可以得到如下的推论. 推论1.3设T∈B(H),则下面的论述是等价的. (1)σ(T)=σSF(T)∪σ0(T). (ⅰ)σ(T+K)=σSF(T+K)∪σ0(T+K); (ⅱ) isoσ(T+K)=σ0(T+K); (ⅲ)σ(T+K)=σ(T)∪E,其中E⊆ρ(T)是至多可数集. 证明(1)⟹(2). 参考引理1.2的证明可得,这里不再赘述. (2)⟹(1). 设λ0∉σSF(T),则T+K-λ0I为半Fredholm算子. 由条件知T+K-λ0I为Browder算子, 则存在δ>0使得B0(λ0,δ)⊆ρ(T+K). 由(ⅲ)可知ρ(T+K)⊆ρ(T), 所以λ0∈isoσ(T)∪ρ(T). 由于T-λ0I为半Fredholm算子,结合引理1.1可知T-λ0I为Browder 算子. 因此σ(T)=σSF(T)∪σ0(T). 注解1.4由引理1.2的证明还可以得到:推论1.3中的(ⅲ)可以替换为accσ(T+K)=accσ(T)∪[isoσ(T)∩σSF(T)]. 引理1.5[8]设T∈B(H)且满足Browder定理,λ0∈isoσw(T),则存在K∈K(H)且K≠0使得λ0∈accσ0(T+K). 注解1.6由引理1.5可以得到下列事实. 设T∈B(H)满足Browder定理. 若对任意非零紧算子K都有isoσw(T)∩accσ0(T+K)=∅,则 (1) isoσw(T)=∅; (2) 对任意K∈K(H)都有isoσ(T+K)=σ0(T+K). 同时,还可以得到下面的推论. 推论1.7设T∈B(H). 若T满足Browder定理且对于任意K∈K(H)都有accσ(T)=accσ(T+K),则 (1) isoσ(T)=σ0(T); (2) 对任意K∈K(H)都有isoσ(T+K)=σ0(T+K); (3)ρw(T)连通. 证明(1) 假设isoσ(T)≠σ0(T),则存在λ0∈isoσ(T)σ0(T). 从而由引理1.1可知λ0∈isoσw(T). 于是由引理1.5可知存在紧算子K0≠0使得λ0∈accσ0(T+K0). 然而据条件可得λ0∈accσ0(T),矛盾. 同理可证得(2). (3) 假设ρw(T)不连通,现取其有界连通分支Ω. 令Γ=∂Ω⊆σSF(T),则由文献[9,引理3.2.6]可知存在K1∈K(H)使得 于是,得到下面的定理. 定理1.8设T∈B(H),则T具有Weyl定理稳定性当且仅当下列条件成立: (1)T满足Browder定理; (2) 对于任意K∈K(H)都有accσ(T+K)=accσ(T). 证明必要性. (1)显然成立. 下面说明(2). 由文献[5,引理2.1]可知:对于任意K∈K(H)都有isoσ(T+K)=σ0(T+K). 假设λ0∉accσ(T+K),则λ0∈isoσ(T+K)∪ρ(T+K),从而T+K-λ0I是Browder算子. 结合(1)可知T-λ0I是Browder算子, 因此λ0∈σ0(T)∪ρ(T), 于是λ0∉accσ(T). 同理可以证得accσ(T+K)⊆accσ(T). 充分性. 任取K∈K(H),设λ0∈σ(T+K)σw(T+K),则T-λ0I是Weyl算子,从而T-λ0I是Browder算子,于是λ0∉accσ(T+K). 由推论1.7可知λ0∈σ0(T+K)⊆π00(T+K). 反之,设λ0∈π00(T+K),再由推论1.7可知λ0∈σ0(T+K), 因此T+K-λ0I是Weyl算子, 于是T+K满足Weyl定理.这样就证明了T具有Weyl定理稳定性. 在这一节中,我们对一类具有特殊谱结构的算子的Weyl定理的紧摄动给出等价刻画. 定理2.1设T∈B(H). 若σ(T)=σSF(T)∪σ0(T),则对于任意K∈K(H){0},T+K满足Weyl定理当且仅当下列条件成立: (1) 对任意K∈K(H){0},accσ(T+K)∪{λ∈:n(T+K-λI)=∞}∪{λ∈σ(T+K):n(T+K-λI)=0}都相同; (2) 对任意K∈K(H){0}都有accσ(T+K)∪[π00(T)∩σb(T)]=accσ(T)∪[σSF(T)∩isoσ(T)]. 证明首先证明必要性. 分以下2种情形来完成. 情形1 isoσ(T)∩σSF(T)=∅. 此时isoσ(T)=σ0(T). 从而π00(T)∩σb(T)=∅且T满足Weyl定理,所以T具有Weyl定理稳定性. 由定理1.8可知对任意K∈K(H)都有accσ(T+K)=accσ(T). 于是(2)得证. 为证明(1)我们断言:对任意K∈K(H)都有accσ(T+K)∪{λ∈:n(T+K-λI)=∞}∪{λ∈σ(T+K):n(T+K-λI)=0}=accσ(T). 由于accσ(T+K)=accσ(T),由推论1.7可知isoσ(T+K)=σ0(T+K),于是 [{λ∈:n(T+K-λI)=∞}∪{λ∈σ(T+K):n(T+K-λI)=0}]∩isoσ(T+K)=∅,即{λ∈:n(T+K-λI)=∞}∪{λ∈σ(T+K):n(T+K-λI)=0}⊆accσ(T+K). 于是accσ(T+K)∪{λ∈:n(T+K-λI)=∞}∪{λ∈σ(T+K):n(T+K-λI)=0}=accσ(T+K). 所以断言得证. 情形2 isoσ(T)∩σSF(T)≠∅. 由注解1.4可知存在K0∈K(H)且K0≠0使得σ(T+K0)=σSF(T+K0)∪σ0(T+K0),isoσ(T+K0)=σ0(T+K0)且accσ(T+K0)=accσ(T)∪[isoσ(T)∩σSF(T)]. 此时容易看出T+K0满足Weyl定理. 类似于情形1可以证明:对任意K∈K(H)都有accσ(T+K)∪{λ∈:n(T+K-λI)=∞}∪{λ∈σ(T+K):n(T+K-λI)=0}=accσ(T+K0). 对于(2),下证对任意K∈K(H){0}都有accσ(T+K)∪[π00(T)∩σb(T)]=accσ(T+K0). 一方面,设λ0∉accσ(T+K0),则λ0∈σ0(T+K0)∪ρ(T+K0). 所以T+K0-λ0I是Browder算子,因此T-λ0I是Weyl算子. 于是对任意K∈K(H){0},T+K-λ0I都是Weyl算子. 由σ(T)=σSF(T)∪σ0(T)及T+K满足Weyl定理可知λ0∉σb(T)且λ0∉accσ(T+K). 于是λ0∉accσ(T+K)∪[π00(T)∩σb(T)]. 包含关系accσ(T+K)∪[π00(T)∩σb(T)]⊆accσ(T+K0)得证. 另一方面,任取K∈K(H){0},设λ0∉accσ(T+K)∪[π00(T)∩σb(T)],则λ0∈isoσ(T+K)∪ρ(T+K). 若λ0∈ρ(T+K),则易知T+K0-λ0I是Weyl算子,从而是Browder的. 于是λ0∈isoσ(T+K0)∪ρ(T+K0),即λ0∉accσ(T+K0). 若λ0∈isoσ(T+K),此时断言λ0∉accσ(T+K0). 事实上,若λ0∈accσ(T+K0),则有λ0∈σw(T+K0). 由λ0∈isoσ(T+K)及σw(T+K0)=σw(T)=σw(T+K)⊆σ(T+K)可知λ0∈isoσw(T+K0). 由于T+K0满足Weyl定理,于是存在δ>0使得σ=B(λ0,δ)∩σ(T+K0)是σ(T+K0)的一个开闭子集,且σ由λ0和T+K0的可数个正规特征值构成. 由文献[6,推论2.2]可知,此时T+K0可分解为 接下来证明充分性. 对于任意K∈K(H){0},下面说明σ(T+K)σw(T+K)=π00(T+K). 设λ0∈σ(T+K)σw(T+K),则T-λ0I是Weyl算子,从而是Browder算子,所以λ0∉accσ(T)∪[isoσ(T)∩σSF(T)]. 由(2)可知λ0∉accσ(T+K),所以λ0∈isoσ(T+K)且0 反之,设λ0∈π00(T+K),分2种情形来讨论. 情形1 isoσ(T)∩σSF(T)=∅. 此时isoσ(T)=σ0(T)且π00(T)∩σb(T)=∅, 于是条件(2)即为:对任意K∈K(H){0}都有accσ(T+K)=accσ(T). 因此λ0∉accσ(T). 则λ0∈σ0(T)∪ρ(T),从而T+K-λ0I是Weyl算子. 情形2 isoσ(T)∩σSF(T)≠∅. 根据引理2.2可知,存在非零紧算子K0使得σ(T+K0)=σSF(T+K0)∪σ0(T+K0)且 isoσ(T+K0)=σ0(T+K0). 由条件(1)可知λ0∉accσ(T+K0),于是λ0∈σ0(T+K0)∪ρ(T+K0),即T+K0-λ0I是Browder算子. 因此λ0∈ρw(T+K). 包含关系σ(T+K)σw(T+K)⊇π00(T+K)得证. 例2.2令H=l2,设T∈B(H)定义为 T(x1,x2,x3,…)=(0,x2,x3,x4,…), 则σ(T)=σSF(T)∪σ0(T),而且accσ(T)∪[σSF(T)∩isoσ(T)]={1}. 定义K0∈B(H)为 K0(x1,x2,x3,…)=(x1,0,0,…). 则K0∈K(H). 通过计算可知accσ(T+K0)∪[π00(T)∩σb(T)]=∅. 于是存在紧算子K0∈K(H){0},使得定理2.1中条件(2)不成立. 因此由定理2.1可知一定存在非零紧算子K,使得T+K不满足Weyl定理. 下面讨论复对称算子的Weyl定理. 首先看一下复对称算子的定义:H上的映射C称为是共轭算子,若C是共轭线性,可逆且C-1=C,并且任给x,y∈H都有〈Cx,Cy〉=〈y,x〉;算子T∈B(H) 称为是复对称算子,若存在H上的共轭算子C,使得CTC=T*. 用S(H)表示H上的所有复对称算子全体. 对复对称算子的Weyl定理,文献[2]给出了非常好的结果. 本文根据上面的结果,继续来研究复对称算子Weyl定理的摄动. 推论2.3设T∈S(H),则对任意K∈K(H){0},T+K满足Weyl定理当且仅当下列条件成立: (1) 对任意K∈K(H){0},accσ(T+K)∪{λ∈:n(T+K-λI)=∞}∪{λ∈σ(T+K):n(T+K-λI)=0}都相同; (2) 存在K0∈K(H)使得T+K0满足Weyl定理,并且对任意K∈K(H){0}都有accσ(T+K)∪[π00(T)∩σb(T)]=accσ(T+K0). 证明由于T∈S(H),则由文献[2,命题2.7]及引理1.2可知,存在紧算子K1满足σ(T+K1)=σSF(T+K1)∪σ0(T+K1)且 isoσ(T+K1)=σ0(T+K1). 显然,T+K1满足Weyl定理. 必要性. 类似于定理2.1的证明可知,对任意K(H){0}都有accσ(T+K)∪{λ∈:n(T+K-λI)=∞}∪{λ∈σ(T+K):n(T+K-λI)=0}=accσ(T+K1). 于是(1)成立. 由定理2.1的证明可知,取K0=K1可得(2)成立. 充分性. 对任意非零K∈K(H),下面说明σ(T+K)σw(T+K)=π00(T+K). 一方面,设λ0∈σ(T+K)σw(T+K),从而T+K0-λ0I是Weyl的. 因为T+K0满足Weyl定理,所以λ0∉accσ(T+K0). 由(2)可知λ0∉accσ(T+K),因此λ0∈π00(T+K). 另一方面,设λ0∈π00(T+K),则λ0∉accσ(T+K)∪{λ∈:n(T+K-λI)=∞}∪{λ∈σ(T+K):n(T+K-λI)=0}. 下面分2种情形进行讨论. 情形1K1=0. 此时有σ(T)=σSF(T)∪σ0(T)且isoσ(T)=σ0(T),则isoσ(T)∩σSF(T)=∅,从而π00(T)∩σb(T)=∅. 于是,条件(2)即为accσ(T+K)=accσ(T+K0)对任意非零K∈K(H)都成立. 若K0=0,则λ0∉accσ(T). 这样就有T-λ0I为Browder算子,从而T+K-λ0I为Weyl算子. 若K0≠0,由条件(1)可知λ0∈π00(T+K0)∪ρ(T+K0). 由于T+K0满足Weyl定理,于是T+K0-λ0I为Weyl算子,从而T+K-λ0I为Weyl算子. 情形2K1≠0. 此时由条件(1)可知λ0∉accσ(T+K1)∪{λ∈:n(T+K1-λI)=∞}∪{λ∈σ(T+K1):n(T+K1-λI)=0},即λ0∈ρ(T+K1)∪π00(T+K1). 由T+K1满足Weyl定理可知T+K1-λ0I是Weyl的,从而T+K-λ0I是Weyl算子. 因此对于任意K∈K(H){0},T+K都满足Weyl定理. 进一步,得到下面的推论. 推论2.4设T∈B(H)且σ(T)=σSF(T)∪σ0(T),则下列陈述等价: (1)T具有Weyl定理稳定性; (2) 对任意K∈K(H)都有accσ(T+K)=accσ(T). 对于复对称算子,也有类似的结论. 推论2.5设T∈S(H),则下列陈述等价: (1)T具有Weyl定理的稳定性; (2) 对任意K∈K(H)都有accσ(T+K)=accσ(T). 如例2.2中定义的算子T,即T∈B(l2)定义为 T(x1,x2,x3,…)=(0,x2,x3,x4,…). 容易验算T∈S(l2). 前面已经证明了存在非零紧算子K,使得T+K不满足Weyl定理,即T不具有Weyl定理的稳定性. 由于accσ(T)=∅,于是由推论2.4或者推论2.5可知,一定存在非零紧算子K0使得accσ(T+K0)≠∅.1 预备知识
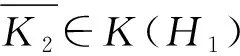
2 主要结论