强GFP-内射模的刻画

◎吴雅丽

(广东交通职业技术学院，广东 广州 510650)

文中的环都为结合环、且有单位元,所有的模都特指左模

内射模是模与环范畴与同调代数理论的一种重要概念，它的研究方法与理论影响涉及代数和其他数学学科但是人们也看到了内射模作为研究工具的局限性，因此产生很多关于内射模概念的推广2009年张力宏和刘岩运用已知的-内射模概念做出-内射模的等价刻画2013年,徐龙玉等人给出-投射模和-投射模是等价的与此同时，他们给出了-投射模对半单环的新刻画

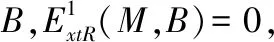
1 强GFP-内射模

11若E为R-模给任意下图模与同态的图形：

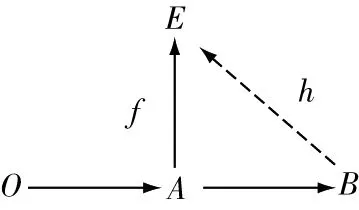
图1

其中底行是正合的,模A是模B的任意有限表现子模,恒能完备为一个交换图,即存在一个模同态:→,使得=|,则称模E是强GFP-内射模

所以，内射模也就是强GFP-内射模在本文参考文献已经给了GFP-内射模的等价刻画,如果A为GFP-内射模，当且仅当对任意自由模F的任何有限表现子模K,有限表现子模K到模A的同态均可以扩张到自由模F到模A的同态由这个等价刻画,可以得出结论：强GFP-内射模为GFP-内射模的一种

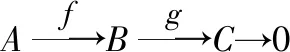
13若E为R-模,下列条件均为等价：

(1)E是强GFP-内射模;

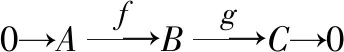
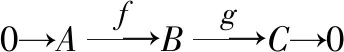
对任意的(,),因为E是强GFP-内射模,所以存在′∈(,),使得′=,即下图可进行交换：

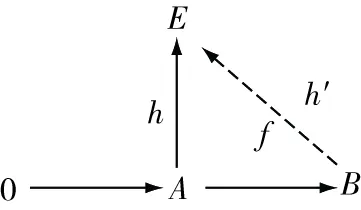
图2

故(′)=′=从而是满同态,所以0→(,)→(,)→(,)→0是正合列

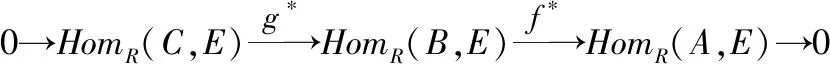
14如果模E是一个有限表现R-模,那么模E是强GFP-内射模当且仅当任何形如0→→→→0分裂的

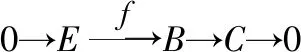
其次证明充分性对于正合列0→→及∈(,),A为有限表现R-模通过本文参考文献[2] 253中定理可以得到充分性结论，下面两行是正合列的交换图:

图3

通过证明，得出正合列0→→→∕→0是分裂的,即存在∈(,),使得=1令=,而===1=因此是强GFP-内射模

结合本文参考文献[2]中介绍的可除模定义，当已知内射模是可除模的一种时可通过证明得出结论：位于交换环上的任意强GFP-内射模，都为可除模

15若R为交换环,强GFP-内射模都为可除模

当模E为强GFP-内射模,且S是R所有非零因子的乘法集时令∈,∈记=(),同时令()=则是一个同态因为是一个非零因子,所以=()是一个自由主理想,从而是有限表现R-模因为模E是一个强GFP-内射模,可推导出可扩张为R到E的同态记作=(1),我们有=()=()=(1)=综上所述模为可除模

与FP-投射模的情形类似，对于强GFP-内射模方面也有下面对应的定理

16([2]定理247)设下图中行是正合列,图中左边的方图可以进行交换:

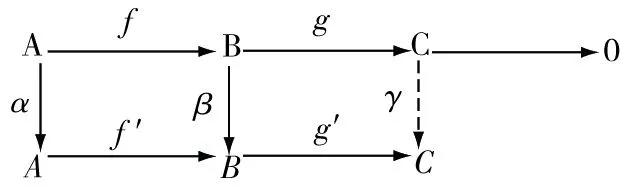
图4

则存在:→′,使得右边方图成为交换图

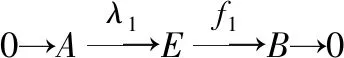
因为模A是一个有限表现R-模，模E是一个强GFP-内射模,因此存在∈(′,),使得=通过引理16得到结论,存在∈(,),使得下图可进行交换:

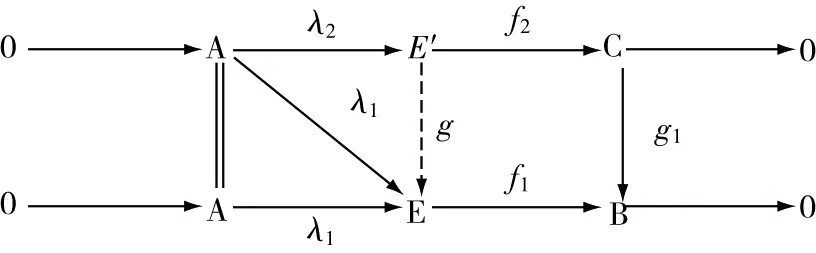
图5

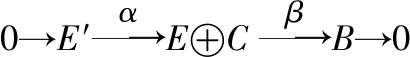
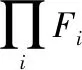
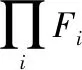
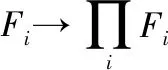
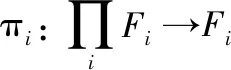
2 强GFP-内射模对环的刻画

下面来看一下强GFP-内射模的等价刻画

21若R为环,下列条件都为等价:

(1)R是一个左G-半单环;

(2)任意R-模都是一个强GFP-内射模;

(3)强GFP-内射模的子模就是强GFP-内射模;

(4)任意一个有限表现R-模，其是内射模

证明(2)⟹(3)任意强GFP-内射模的子模是R-模,从(2)可知,任意强GFP-内射模的子模，均为强GFP-内射模

(3)⟹(2)对任意R-模C,C是其内射包E(C)的子模,故C是强GFP-内射模

(2)⟹(1)对任意R-模C,B是C的有限表现子模.由(2)知B是强GFP-内射模,故对恒等映射1∈(,),存在∈(,),得出=1,其中:→是一个包含映射所以正合列0→→→→0是分裂的因此B是C的直和加项

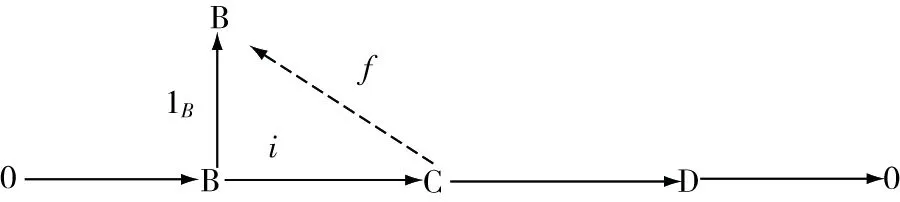
图6

(1)⟹(4)设B为有限表现R-模,由于条件B是其内射包E(B)的直和加项,因此B是内射模

(4)⟹(1)对任意R-模C以及其有限表现子模B,存在正合列0→→→∕→0,因为条件B是内射模,所以该正合列分裂得到结论B是C的直和加项

当R是一个左Noether环时,R是一个左G-半单环当且仅当R是一个半单环如果一个R-模M的任意子模都是它的直和加项,可推导出M为半单模如果R自身的模为半单模，继而R为半单环.最终可以得出结论，当且仅当每个R-模都是内射模或每个R-模都是投射模时，R为半单环

22若R为一个左Noether环,下列条件都为等价:

(1)R是半单环;

(2)任意的有限表现R-模都为内射模

(1)⟹(2)显然

(2)⟹(1)设I是R的左理想,因R是左Noether环,所以I是有限生成的,因此I是有限表现模；因I为内射模,可以得知正合列0→→→∕→0分裂从而可以推导出I是R的直和加项，而R则是半单环

23([3]定理27)设R为左凝聚环,下列条件均为等价:

(1)环R不仅为左自内射环，同时也为VN正则环;

(2)环R为左G-半单环;

(3)环R为左自内射环，且每一个R-模都为GFP-内射模

由引理23可知,若为左凝聚环,每个模都是强GFP-内射模的条件为当且仅当是VN-正则环且是左自内射环