数形结合思想在初中数学解题中的应用

◎刘亚军

(甘肃省天水石马坪中学，甘肃 天水 741000)

数学是一门实用性非常强的学科，学习数学知识可以解决实际生活中的一些问题同时，数学知识也是难度较大的学科，尤其是步入初中之后，作为小学与高中的衔接，初中数学知识在难度上有一个较大的跨越，很多学生一开始学习数学还会比较轻松，但随着时间推移就会越发的力不从心到了这个时候，正确的解题方式就显得尤为重要数形结合本就属于一个高效解题思维，它可以将复杂的数学问题简单化通过图表形式表达问题含义，可以加强学生的逻辑能力，深化对问题的思考

一、数形结合思想在初中数学解题应用中的作用

(一)促进学生发展思维能力

学生步入初中后，整个数学知识的难度加深，问题也变得越来越复杂，学生在解题时会出现力不从心的现象在初中数学解题中使用数形结合思想，有利于学生简化难度较大的数学问题数形结合思想简化问题主要表现在数量之间的关系，以及图形之间能够互相补充和转化

将数形结合思想运用在解题中，可以提升学生的审题能力以及答题思维，并在一定程度上增强学生的观察力和注意力对此，教师在教学过程中应该持续向学生传输数形结合思想，不断发展其数学思维

(二)激发学生学习兴趣

数学问题难度大是影响学生学习数学兴趣的主要因素之一为了改变这一现象，教师在教学数学知识时应该主动使用数形结合思想，利用该思想引起学生注意力，让学生学会在数学学习中寻找乐趣，同时降低学生数学学习的难度，让学生主动接受数学知识，进而提升整体学习质量

解决数学问题时，在解题思路中加入数形结合思想，能够让学生感受不一样的体验，同时也会促使学生主动与教师和同学探究相关问题，激发自身学习欲望，提高学习激情，强化学习质量，完成教学目标

二、数形结合解题思想在初中数学中的初步应用

(一)有理数教学中的应用

在初中数学教学中，有理数是其中相对来说比较重要的一部分内容在进行有理数教学时，教师可以结合数形思想，利用数轴的形式进行表达，使其在数与形之间进行有效转换，以此帮助学生更好了解与数轴相关的知识另外，数轴不仅可以帮助学生掌握有理数的绝对值、相反数等概念，还能在数轴上进行数字的大小比较在学习有理数时，数轴还可以使用在解题方面实际上，数轴已经成为当前数学教学中的一个重要辅助工具，灵活使用数形结合思想，能够使数学问题变得更加简单化

(二)问题分析中的应用

初中阶段的学生不管是在思维上还是认知能力上都远超小学阶段，并且有了较大进步，他们可以凭借自己的思维模式独立面对并解决一些数学问题，对问题进行分析，并抓住其中的重点内容进行解答在图形认知上，他们有一定的把握，小学时期的学习也为其奠定了基础在这样的情况下，当初中教师在引导学生学习数学知识时，就可以全面发挥这种教学优势，并合理应用他们已经有了一定基础的图形意识，实现在数学教学中的图形转化，同时与数学知识建立相关联系，这非常有利于提升学生的数学学习能力尤其是在教学一元一次函数的图形以及平面直角坐标系中，使用数形结合思想能够起到非常大的作用

(三)应用题的应用

除了上述两点之外，应用题在初中教学中的占比也相对较大在分析应用题时能够发现初中学生学习中的漏洞，还能了解学生是否缺失应用能力为了解决学生应用题解决能力较弱的现象，教师可以在教学过程中引入数形结合思想，让学生学会使用数形结合思想真正解决数学问题，从而提升自己的应用题解决能力

三、利用数形结合思想强化学生数学解题能力

(一)数形结合思想——利用数轴解决问题

不等式问题可以通过数轴的形式加以解决在初中数学学习过程中，不等式也是一个相对较为重要的知识内容，主要教学目的是使学生独立解决一元一次不等式，并使用数轴形式表达出不等式的集，这是典型的数形结合问题在解答一元一次不等式的问题时，首先要注意未知数的前面为负系数时，要改变不等式符号的方向；其次，带等于符号的不等式用实心点表示，反之用空心点表示

比如：不等式-2≤<1的解集可以通过哪个数轴表示？( )

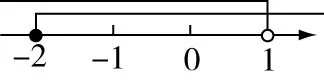
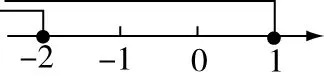
如上图，在解答不等式解集时，为了更加清楚的在数轴上找到不等式的解集，主要观察后面的式子为空心，以前面式子方向为准，此题选择A

除了使用数轴解决这一问题，还能通过数轴的形式解决中位数和众数的问题按照从小到大的次序依次将变量排好，处于该数轴正中间的数就是中位数，而出现次数最多的变量就是所谓的众数这也是数学中较为多见的概念中数只需要排列数据，而众数则要进行统计，学生通过数轴理解两个数的含义更明了

(二)数形结合思想——通过直角坐标系解决问题

函数贯穿了整个初中数学教学过程，其中包括一次函数、二次函数等一系列函数内容同时，函数也是一个较为复杂的知识，解题时需要学生具备较强的逻辑性思维，使用的解题方式多数是数形结合在解决函数问题时要绘制出相关的函数图像，从而使原本较为复杂的问题简单化、形象化，同时还要了解函数关系式中参数的作用，另外教师在教学过程中还要引导学生了解什么是函数关系以及函数的类型，要求学生一看到题目就能了解该题型是什么类型的函数问题，即使问题中没有自带函数图形，学生也可以根据函数类型绘制出相关的函数图像，解决数学难题

图1

在解答相关类型的问题时，有4个关键点，其一，观察开口方向；其二，观察对称轴；其三，观察定点坐标；其四，观察特殊点本题虽然没有告知的系数，但通过题干了解到=+3与轴相交，那就可以知道为(0,3)，过点且平行于轴的直线为=3；另外，=3上三个点的纵坐标相同，以此推算出和分别为(-3,3)、(3,3)，从而计算出最终答案为6

在初中数学教学中，函数是非常重要的内容，不仅是初中数学教学的重点，更是其中的难点函数自身就是一个纯代数意义的概念，有很多可以用来表示函数的方法，比如，列表法、解析法等，但这些表示方法很难为学生带来直观的感受，更无法帮助学生理解知识在这样的形式下，只会加大函数的学习难度但将图形结合运用其中，必然会取得事半功倍的效果

如，求方程--1=0的解

方法一：利用一元二次方程的求根公式进行解答

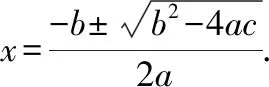
方法二：变形题目中给予的方程式=+1，之后绘制出函数图像(图2)：=+1与=，需要求出的方程的解就是两个函数图像的交点

图2

(三)数形结合思想——使用图形解决实际问题

图形可以解决以上问题，还可以解决概率问题，可以利用绘制树形图的形式简化数学问题

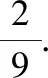
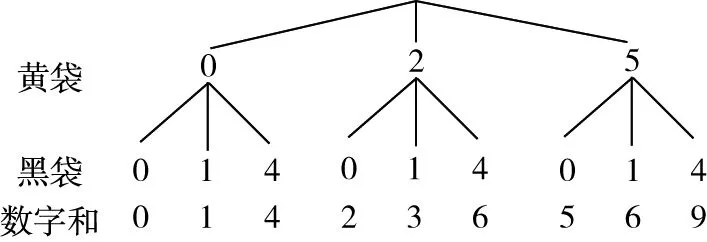
图3

另外，通过数形结合还能解决与三角形相关的问题，在使用数形结合解答三角形问题时，最关键的是将问题转化成直角三角形的问题

比如，一个晾衣架的支架长度都为108厘米，∠为59°，请问晾衣架两个支架点的距离为多少？(保留一位小数)

结合图4，可以知道△是一个等腰三角形，过点，做的垂直交于，因此为三角形的中线，在直角△中，解出，则=2=2sin∠=1123厘米最后需要注意的是要作答，因为该题是应用题

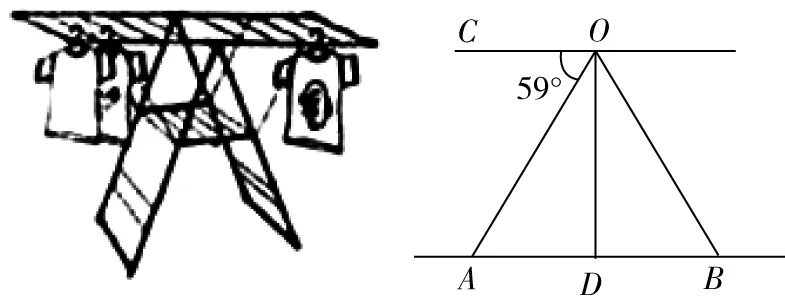
图4

初中阶段的数学题相对小学阶段的数学题来说，难度更大，题目给出的条件相对复杂为了能够有效解决数学问题，教师可以引导学生使用数形结合的方式寻找问题的突破口

比如，如图5所示，一名安装工人站在梯子上准备为房子的天花板安灯，已知天花板与地面之间的高度为29米，梯子的两个矩形面的长由六条踏板将其分成了七分，两个梯脚之间的长度为1米(固定)，矩形面与地面之间的夹角为78°假如安装师傅的身高为178厘米，要想保证整个安装过程师傅的状态最舒服，天花板与师傅头顶之间的距离要保持在005～020米此刻安装师傅站在第三个安装梯的踏板上，是否符合安装方便的条件？

图5

教师可以使用数形结合的方式，将应用题的意思进行展示，如图6所示，这样学生就可以在短时间确定解题思路数形结合思想要结合不同的问题，进行合理运用，才能有效提高解题的效率和质量另外，教师在引导学生解题时，还要尝试将数学题与实际生活结合，锻炼学生解决实际问题的能力

图6

(四)数形结合思想——解决比较字母大小的问题

一般来说，可以使用函数图像或者是数轴的方式比较字母之间的大小关系，但这样的方式相对来说比较麻烦有些字母大小的问题可以通过函数与方程之间的关系，使用数形结合的方式进行解决

比如：,是方程(-)(-)=1(<)的两个根，且<，请问实数,,,之间的大小关系：________

解析：已知与是方程(-)(-)=0的两个根，那么可以将其看作抛物线=(-)(-)和轴的两个交点的横坐标，而(-)(-)=1的根可以看作是=(-)(-)-1这一抛物线和横轴两个交点的横坐标将=(-)(-)向下平移1个单位，则可以得到=(-)(-)-1，如图7所示，最终得出<<<

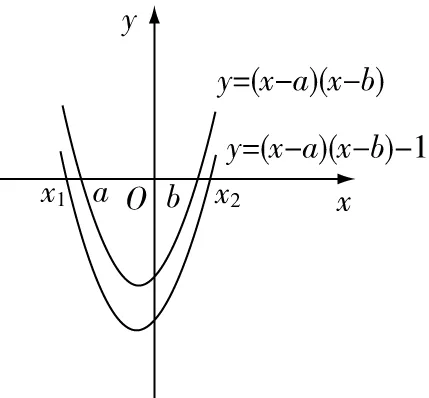
图7

结束语

综上所述，数形结合思想在初中数学解题中占据非常重要的位置，因此，教师在传授数形结合思想相关的内容时，也要注意引导学生对一些可以使用数形结合思想的问题进行探究，让学生在问题中发现数形结合思想的价值，从而转化成自己的解题价值观，主动使用数形结合思想解决更多的数学问题，提升学习效率，进一步提升数学成绩