抓图形对称显互逆本质，借知识类比促能力迁移——“对数函数及其性质”教学设计

◎张丽丽

(深圳市坪山高级中学，广东 深圳 518000)

一、教学设计思想

本节课通过互化，学生从形式上理解指数函数与对数函数的关系；通过作图和对折，学生从实质上理解指数函数与对数函数之间的转化关系通过复习回顾指数函数的相关性质，借助指数函数与对数函数的相互转化关系，类比、总结、归纳对数函数的性质，培养学生知识迁移的能力

二、教学分析

1教材分析

函数是高中重要的知识模块，“对数函数及其性质”是高中数学函数知识中的一个重点内容，也是在解决实际问题时常见的一种函数模型通过学习指数函数与对数函数的概念，培养学生树立对立统一、相互联系、相互转化的数学思维通过对知识进行迁移，培养学生类比推理、迁移知识的基本数学能力

2学情分析

学习本节课之前，学生已经学过了函数的基本概念和性质，掌握了一定的学习函数的基础知识，为后面深入学习和研究基本初等函数及其性质夯实了基础在前面的学习中，学生通过学习具体的指数式和指数函数，储备了研究函数概念和模型的一些基本方法和步骤；又通过学习对数与对数的运算，了解了指数式和对数式之间相互转化的关系，从而为本节课“对数函数及其性质”的学习提供了基本的知识储备

三、教学目标

【知识与技能】

1理解对数函数的定义，掌握对数函数的图像和性质；

2能运用图像和性质解决有关求定义域、比较大小、过定点等问题

【过程与方法】

1经历指数函数与对数函数关系探究的过程，体会通过互化从形式上理解指数函数与对数函数的关系，通过作图和对折从本质上理解指数函数与对数函数之间的转化关系，掌握从特殊到一般、数形结合的数学思想；

2通过指数函数概念和性质的学习，类比对数函数的概念和性质的学习，培养类比、分析、归纳推理能力

【情感态度与价值观】

1通过指对关系的学习，树立相互联系、相互转化的观点，培养学生的探究意识和进取精神；

2通过指数函数相关知识的迁移，感受理论与实践的统一，培养严谨的思维品质

四、教学重点

1对数函数概念形成的过程；

2指数函数与对数函数之间关系的理解；

3对数函数性质的形成过程及灵活运用

五、教学流程

六、教学过程

环节1：情境引入

引例1：《指数、对数、幂函数诗》

晨雾茫茫碍交通，蘑菇核云蔽长空；

化石岁月巧推算，文海索句快如风；

指数对数相辉映，立方平方看对称；

解释大千无限事，三族函数建奇功

【设计意图】诗歌引入，形式新颖，易于引起学生注意，激发探究的欲望通过这首函数诗，带领学生感受函数在不同形态下的别样魅力

环节2：对数函数的概念

1引例探索

引例2：将下列指数式化成对数式

思考1：①②是指数式，对应的是对数式；③④是具体的指数函数，其对应互化后的函数是具体的对数函数吗？⑤是一般形式的指数函数，其对应的函数是一般形式的对数函数吗？若不是，又该如何化成对数函数？

【设计意图】具体和一般形式的指对互化，通过类比进行知识迁移

2形成概念

类比指数函数的概念，总结对数函数的概念

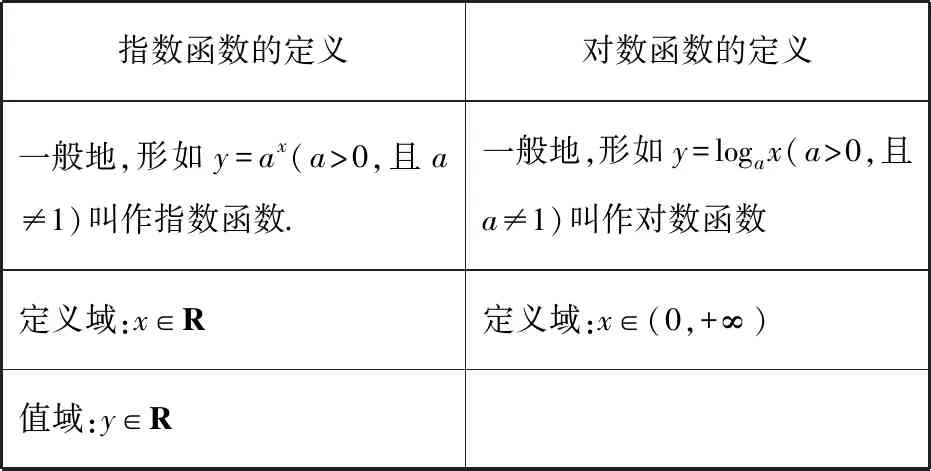
指数函数的定义对数函数的定义一般地,形如y=ax(a>0,且a≠1)叫作指数函数.一般地,形如y=logax(a>0,且a≠1)叫作对数函数定义域:x∈R定义域:x∈(0,+∞)值域:y∈R

【设计意图】类比指数函数，探究对数函数的概念

3概念辨析

引例3：判断下列函数是否是对数函数

(1)=2log;

(2)=log+1;

(3)=log(2+1);

(4)=log3;

(5)=log

变式：若函数=(-3+3)log是对数函数，求的值

【设计意图】通过典例强化对对数函数概念的内涵和外延的理解，通过变式训练加强巩固

环节3：指数函数与对数函数的关系

1分析与验证

思考2：观察下列变化过程，

【设计意图】通过互化，引导学生从形式上感受指数函数转化为对数函数的本质，即通过自变量与函数值之间的对调，得到对数函数形式，从而在本质上进一步理解指数函数和对数函数互逆的本质特征

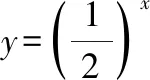
【设计意图】通过在网格纸上描出上升和下降型的两个指数函数图像上的几个具体的点，再描出它们关于=对称的点，再进一步将点连接形成图形，从而得到相应对数函数的图像主要从数据特征方面去理解指数函数与对数函数互逆的本质特征，达到对知识深刻的理解

2探索与总结

思考4：动手折叠，探索所画图形具有怎样的对称性？

【总结】通过找对称点、动手作图、折纸探索，发现指数函数与对数函数图像对称关系的本质知道具有这种对称关系的函数互为反函数

【设计意图】透过表象看本质，引导学生深入探究问题的本质通过动手作图，折纸验证猜想，培养学生的探究欲望和实践能力

环节4：对数函数的性质及应用

1性质探究

复习指数函数的有关性质，类比归纳总结对数函数的性质，完成下面的表格：

函数y=ax(a>0,且a≠1)y=logax(a>0,且a≠1)图像0101定义域值域过定点单调性关键点渐近线

2性质运用

引例4：求下列函数的定义域

(1)=log(4-)；

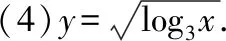
引例5：函数=log(-1)+2 (>0,且≠1)的图像恒过定点

引例6：比较下列各题中函数值的大小

(1)log34和log85；

(2)log0318和log0327；

(3)log51和log59(>0,且≠1)；

(4)log3和logπ

变式：设=log2,=log2,=log3，则,,的大小关系为

【设计意图】通过类比指数函数的图像和性质，归纳对数函数的图像和性质，有助于学生深刻把握指数函数和对数函数之间的关系

环节5：课堂小结

(1)通过本节课的学习，你学到了哪些知识？(知识)

(2)在本节课的学习中，你用到了哪些思想方法？ (思想方法)

(3)通过本节课的学习，你的哪些能力得到了提升？(能力)

【设计意图】通过问题式的总结与反思，促进学生对学习过程的概括和对已有知识的重组

七、教学反思

1设计有灵魂

(1)诗歌引入见奇效

本节课用函数诗进行引入，既从宏观上展示了高中阶段三大基本初等函数及其在生活中的应用，又在细节上描述了指数函数和对数函数间的关系，为后续借助指数函数来研究对数函数提供了方向，同时展示了数学的文化魅力和人文价值，有利于激发学生的学习兴趣

(2)从特殊到一般

从学生熟悉的指数式和对数式的互化入手，符合教育学中的最近发展区理论，将特殊的指数式及指数函数式互化为相应的对数式，既有利于获得学生的认同感，又加深学生对指、对关系的深入理解

(3) 类比充分记忆深

充分利用类比的方法，类比研究指数函数的模式研究对数函数，类比学习归纳指数函数的图像和性质的方法，归纳总结对数函数的图像和性质，既达到对本节课内容的理解，又巩固深化了研究函数的基本模式和方法

(4)巧抓对称特征，凸显互逆本质

在完成具体的指数式和对数式互化后，通过作函数图像(列表、描点、连线)，从图形上理解指、对函数间的关系，抓住图形对称特征，深入理解指数函数与对数函数间对称关系的本质

2方法有创新

(1)问题促思考

在指对互化式环节中，以提问的形式促进学生思考，既能快速抓住学生的注意力，又能引导学生学会思考、学会研究、学会领悟，有利于学科核心素养的培养

(2)动手实践显本质

通过列表、描点、连线作图，动手折叠观察图形的对称关系，学生体验到发现的乐趣，培养学生实践和探究的精神

3效果有检测

总结得出对数函数的概念后，为了帮助学生理解定义式，教师设计了例题和变式，检测学生对概念学习和理解的效果；类比指数函数的图像和性质的学习，总结归纳出对数函数的图像和性质后，要求学生学会换位思考，站在命题者的角度思考可供考查的知识点，通过设计配套的例题，检测学生对性质的理解和灵活运用

4小结有层次

课堂小结从知识、思想方法和能力三个维度进行总结提炼，既帮助学生将本节课的内容进行了再次强化，又站在一定的高度思考，从而提升了学生的思维水平在能力提升方面，借助对数函数的学习，加强与前面所学知识间的联系，对数函数与对数式是一般与特殊的关系，对数函数与指数函数既平行又相关，指数函数和对数函数又都是函数，当然符合函数的研究模式，在具体的知识点考察时又与第一章集合的运算紧密相连，从而达将高一目前所学的知识进行融会贯通的目的

对数函数及其性质是高中学习的一个难点又是一个重点，通过建立跟指数函数的关系，抓住图形之间的对称关系，阐明二者互逆的本质，即有利于帮助学生理解和掌握知识，又能够培养学生类比迁移的能力