二次型理论对中学数学的指导作用

◎李欣欣

(广西师范大学数学与统计学院,广西 桂林 541006)

一、前言

德国教育家克莱因的著作《高观点下的初等数学》主张教师应在“高观点”的站位下审视中学数学内容,学懂弄透数学网状体系,指导学生了解各个学段所学的数学并非孤立的,而是相与为一的所谓“高观点下的初等数学”不是肆意忽视学生原有的认知水平，直接将高等教育知识强行堆砌,而是将高等数学的思想和方法服务中学数学，这就要求职前教师在师范生阶段要学好高等数学,掌握知识体系的内在逻辑,不仅要学习“高观点”的“术”,还应强化“道”的吸收,从而更好地推动今后教师专业的发展反观现实,职前数学教师认为高等数学与初等数学衔接性不强,在学习高等数学时存在敷衍应付的情况但他们这种想法是错误的,数学学习不是间断的,而是有逻辑的、螺旋上升的,学好高等数学能对数学知识内涵的把握更加到位,掌握的数学高观点思想方法亦可以指导中学数学教学

高等数学中的二次型理论起源于几何学中二次曲线方程和二次曲面方程化为标准型问题的研究,是矩阵理论的应用二次型可作为解决代数问题的着手点,对中学数学代数问题有极大地指导作用在中学数学学科中,多元函数求极值和最值、不等式证明、多项式因式分解、判别二次曲线形状等问题可借助高等数学中二次型相关理论及性质来优化其解法鉴于此,本文在简单介绍二次型理论及其性质的基础上,厘清高等数学中二次型与初等数学代数等内容的内在联系,深化相关习题解法,助推职前数学教师更便捷、更高效、更实在地运用二次型解决中学数学教学难点,将二次型应用于中学数学教学

二、二次型的基本定义

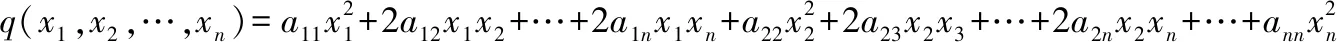
2(,,…,)=都可由任一元二次型(,,…,)唯一地转换表示,这里的=(,,…,),且二次型(,,…,)的矩阵是对称的,(,,…,)的秩也叫的秩

三、二次型在中学数学中的应用

(一)相关定理

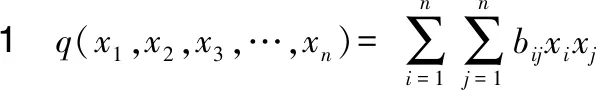
1若是函数()在某稳定点处的何塞(Hesse)矩阵,有：

(1)当正定时,()在处取得极小值；

(2)当负定时,()在处取得极大值；

(3)当不定时,()在处非极大值亦非极小值

注:当是半定(半正定,半负定),()在处可能有极值,也可能没有极值

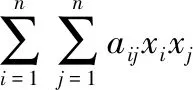
同时有如下规律

1正定、半正定方面：

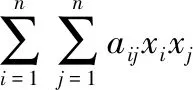
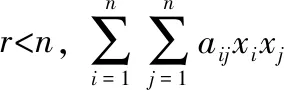
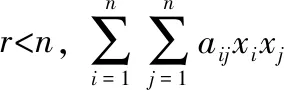
2负定、半负定方面：

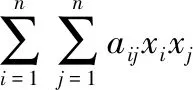
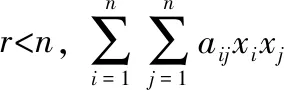
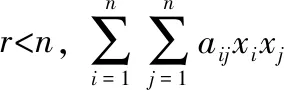
3不定方面：

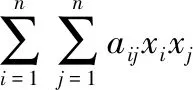
根据定理2，我们了解了判断函数是否有极值、是有极大值还是极小值的一般方法

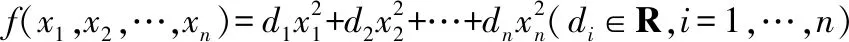
3当一个实二次型的秩为2且符号差为0,或秩为1的情况时,此实二次型便可分解成2个实一次齐次多项式的乘积

(二)求多元函数的极值

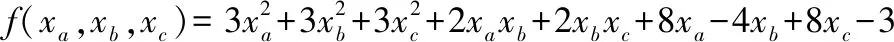
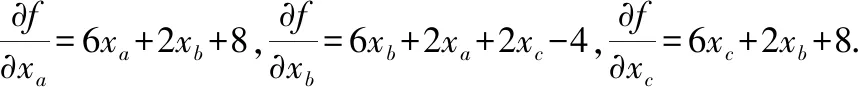
解此方程得稳定点(-2,2,-2),命名为点

在点(-2,2,-2)处,对函数进行二次偏导,有

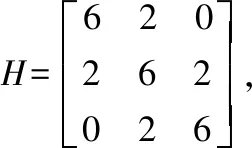
此时Hesse矩阵中的各阶顺序主子式的情况如下，

一阶：|6|=6>0，

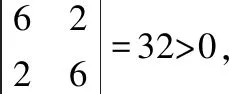
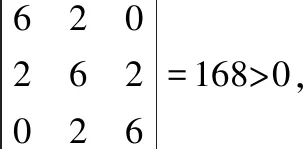
所以根据定理1可知,Hesse矩阵正定

又由引理1可知,有极小值,且在点(-2,2,-2)处取得到,经过代入法算得,的极小值为(-2,2,-2)=-23

(三)求多元函数的最值

对于求二次函数的最值问题,我们可以根据该二次型矩阵的特征值来求,这种方法帮助我们化繁为简

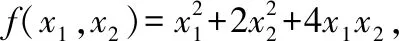
当中学生没有学到用二次型性质求最值的问题解法时,他们通常会用如下的方法解题

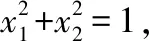
此时相当于cos,相当于sin所以(,)=(cos,sin)

()=cos+2sin+4cossin=1+sin+2sin 2,

由于cos 2=cos-sin=1-2sin,

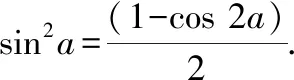
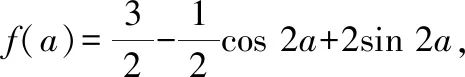
′()=sin 2+4cos 2=0,即sin 2=-4cos 2

又因为sin2+cos2=1,

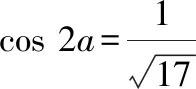
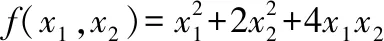
现在我们来看第二种解法,依托二次型矩阵以及其对应的特征值来解决

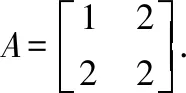
那么其对应的特征多项式为

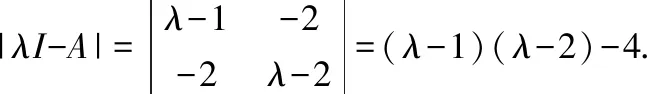
现求对应的特征值,即令-3-2=0

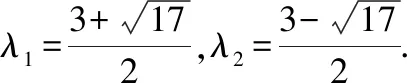
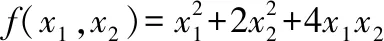
(四)证明不等式

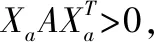
3求证9++3>2-4-2(其中,,是不全为零的实数)

把不等式移项,即需证9++3-2+4+2>0

令二次型(,,)=9++3-2+4+2,下证>0,即证为正定二次型

易知此二次型的矩阵为

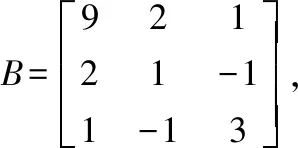
因为的各阶顺序主子式：

一阶：|9|=9>0，

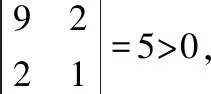
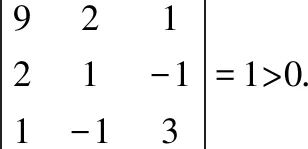
所以,根据定理1,知是正定的,故>0即有9++3>2-4-2成立,其中,,这些实数不全为零

(五)多项式因式分解

4把--2-1分解因式结果正确的是( A )

A.(++1)(--1)

B.(+-1)(--1)

C.(+-1)(++1)

D.(-+1)(++1)

中学生的普遍做法是把选项一一展开计算后,对比原式,选出答案现用二次型的性质解决此问题,首先我们判断该二次型可否分解,如果可以则进行分解

令(,)=--2-1,(,,)=--2-

那么就有关系式(,)=(,,1)成立,

下面考虑(,,)=--2-的秩和符号差,

首先对(,,)=--2-作非线性替换，

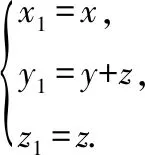
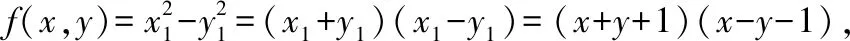
(六)判断二次曲线的形状

5化简++7-8-+15=0,如它是一个封闭图形,计算其面积

令(,)=++7-8-+15

现令(,,)=++7-8-+15

那么,(,)=(,,1)

现对(,,)进行非线性替换

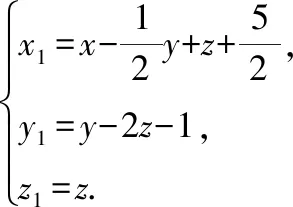
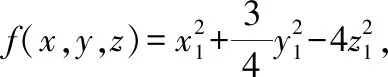
四、结束语

本文归纳总结了二次型理论及其性质对中学数学的指导作用,主要涉及求多元函数的极值与最值、证明不等式、分解因式、判断二次曲线的形状等内容,以期为中学数学教学提供参考与灵感其实在中学课堂上,并非所有相关类型题都适合用高等数学中的“二次型”思想来解决,我们要依据学情而定但是，我们由此可以知道,初等数学与高等数学是一脉相承、蕴含逻辑关系的知识体系

职前数学教师接受高等数学知识，其意义不是为了考试通关,而是致力于提升未来数学教师的专业理论知识及数学素养,能用“高观点”思想来指导中学数学教学与科研工作,因此，助推职前数学教师注重高等数学与中学数学的衔接非常有必要在遇到一些用中学思想较难解决的习题时,中学数学教师可选取合适的“高观点”内容合理衔接高等知识与初等知识,在学生能理解的难度变化范围内,让学生体会到数学的奇妙