热力学数据对1, 3-丁二烯燃烧特性的影响
任娜娜, 薛洁, 王治钒, 姚晓霞, 王繁
热力学数据对1, 3-丁二烯燃烧特性的影响
任娜娜1, 薛洁1, 王治钒2, 姚晓霞3, 王繁1
(1. 四川大学原子与分子物理研究所, 成都 610065; 2. 成都工业学院电子工程学院, 成都 611730; 3. 四川大学化学工程学院, 成都 610065)
基于G4方法, 计算了1,3-丁二烯框架燃烧反应机理中102个物种的热力学数据, 并考察了振动非谐性、 频率校正因子以及受阻内转动对结果的影响. 结果表明, 考虑振动非谐性或采用不同的频率校正因子, 对热力学数据的影响不大; 考虑内转动后, 对热力学数据有较大影响. 而且考虑内转动后, 得到的热力学数据与实验热力学数据吻合得更好. 用所得热力学数据模拟了1,3-丁二烯的绝热燃烧温度以及点火延迟时间, 结果显示, 要得到可靠的绝热火焰温度, 对小分子(如CO和CO2等)的热力学数据需要采用实验结果. 将用所得热力学数据模拟得到的点火延迟时间, 与机理本身的热力学数据所得点火延迟时间进行对比, 二者差别显著, 表明所得热力学数据主要通过改变一些反应的逆反应速率常数来影响点火延迟时间. 进一步确定了用所得热力学数据对点火延迟时间有显著影响的一些物种.
热力学数据; 非谐性; 频率校正因子; 受阻内转动; 燃烧反应机理
燃烧反应动力学机理对于理解并控制燃烧过程以及飞行器燃烧的数值模拟都至关重要. 燃烧反应动力学机理包含燃料燃烧过程中的化学反应以及这些反应的动力学数据、 所涉及组分的热力学数据和输运数据. 虽然燃烧机理研究一般集中于改进反应路径以及优化反应速率常数, 但燃烧模拟结果对热力学数据也很敏感. 热力学数据用于计算逆反应的速率常数、 反应的平衡常数以及所释放的热量. 由于热力学数据对能量平衡和化学平衡的重要影响, 可靠的热力学数据对于准确预测化学反应速率、 构建反应机理、 利用燃烧反应动力学机理预测燃烧特性等均非常重要[1~3]. Bugler等[4]基于高精度的从头算理论和在线数据库中的数据得到了C5物种的热力学数据, 与用基团加合法得到的热力学数据对比, 发现更新后的热力学数据对烷烃的低温点火延迟时间有显著影响; 随后他们[5]采用组合方法G4结合原子化焓的方法, 计算了60种含氮化合物的标准生成焓, 其中, HNO2的标准生成焓与Mathieu和Petersen等[6]的结果相差14.9 kJ/mol, 这导致由HONO生成HNO2的异构化反应的逆反应速率常数在298.15 K时的差异超过900倍, 且在一维火焰的模拟中N2O浓度减少20%, NO2浓度增加了约20%. 此外, Mohamed等[7]使用Benson等[8]提出的基团加和法(GA)改进了2-甲基己烷燃烧模型中的热力学数据, 其中, RO2自由基在298.15 K时的生成焓与原始生成焓相差10.9 kJ/mol、 熵相差5.4 J·K‒1·mol‒1, 改变这些热力学数据后, 2-甲基己烷在负温度系数(NTC)区的反应性降低. 同时Lehn等[3]优化了Mohamed提出的2-甲基己烷机理(2-MH)中的生成焓, 其优化前后的差别约为5 kJ/mol, 模拟得到的点火延迟时间差别达到20%. 这些结果都显示了在动力学模型中使用可靠的热化学值的重要性.
获得准确可靠的热力学数据一直是许多燃烧模拟研究的主要目标之一. 近年来, 常用的热力学数据库包括由Ruscic等[9,10]提出的活性热化学表(The Active Thermochemical Tables, ATcT)以及CCCBDB-NIST[11]和NIST-JANAF[12]数据库等. ATcT为准确确定物种的热化学性质提供了一种非常有效的方法. 这种方法涉及到一个热化学网络, 其中包括超过1300个有机物、 自由基以及一些与燃烧和空气污染相关的无机物的实验值和高精度的理论值, 但ATcT中仅给出了这些物种在0和298.15 K下的标准生成焓[13~15]; CCCBDB-NIST给出了一些物种在0和298.15 K温度下的谐振频率、 几何结构、 生成焓、 热容和熵的实验值. NIST-JANAF提供了少量分子在不同温度下的生成焓、 热容和熵的实验值. 此外, Goldsmith等[16]最近报道了超过200种与燃烧相关的物质的热力学值. Verevkin等[17]收集并评估了烷烃、 烯烃、 炔烃、 烷基苯、 烷醇、 醚、 酮和醛、 羧酸、 酯及碳酸盐的生成焓. Burke等[18]汇编了碳氢化合物燃烧涉及的C1~C4小分子或自由基体系的热力学参数, 对这些参数的不确定性进行了分析并给出推荐值. 值得注意的是, 这些研究很多只给出了稳定小分子的热力学性质.
在实际构建机理中, 常常采用基团加和法计算机理中物种的热力学数据, 但是这个方法对一些物种热力学数据可能存在较大误差. 基于从头算电子结构理论结合统计热力学方法为预测热力学数据提供了另一种方法. 目前, 高精度的计算方法包括Weizmann-n系列方法[19~22]、 高精度外推从头算热化学方法(HEAT)[23~25]、 焦点外推方法(Focal-point analysis, FPA)[26~30]、 Feller-Peterson-Dixon(FPD)方法[31~34]和Klippenstein的ANL-n的方法[35]等, 其中, Weizmann-n, HEAT, FPA和FPD方法对于小分子生成焓的计算精度可达±2 kJ/mol, 可用于计算C0~C3燃料燃烧机理中重要物种的热力学数据, 也为其它方法计算热力学数据提供了参考值. Klippenstein等[35]用ANL-n方法计算了0 K下150个物种的生成焓, 与ATcT实验值相比, 生成焓的计算误差小于5 kJ/mol. 这些高精度方法都采用了外推到完备基组的CCSD(T)计算, 只能用于计算包含几个重原子的小分子体系[36]. 对于较大体系的分子, 通常采用组合方法[如CBS系列方法(CBS-QB3, CBS-APNO)[37~39]和Gaussian-系列方法(G3, G4)[40~42]], 其中G4方法的能量精度在4 kJ/mol以内, CBS-QB3方法能量精度在6.3 kJ/mol之内. 最近Simmie等[43,44]分别用CBS-QB3, CBS-APNO, G3, G4和W1BD等组合方法, 计算了45个CHO稳定分子和38个CHO自由基的标准生成焓, 发现其计算精度顺序为G4>G3>W1BD>CBS-APNO>CBS-QB3. 此外, Wilson等[45]用等键反应方法结合组合方法G4, G3和G3(MP2), 计算了60种碳氢化合物的标准生成焓, 其中, G4方法所得结果的平均绝对偏差(MAD)最小(4.89 kJ/mol). 这些结果表明, G4是一种可靠的计算中等尺度分子热力学数据的方法.
要得到高精度的热力学数据, 通常还需要考虑分子振动的非谐效应, 目前, 常用的计算非谐频率和非谐振动零点能的方法是振动二阶微扰理论(VPT2)[46~49]. 在一些热力学数据的高精度计算方法(如HEAT, W4和ANL-n方法等)中, 基于DFT, MP2或CCSD(T), 用VPT2所得的非谐频率计算物种的热力学数据. 研究也表明, 在得到非谐振动频率后, 结合谐振近似的配分函数计算热力学性质, 能改善计算结果[50,51]. Li等[52]研究了非谐性对C5~C8烷烃的生成焓、 热容和熵的影响, 结果表明, 非谐校正对这些热力学数据略有改善. 对于较大体系, VPT2的计算通常非常耗时. 实际计算中, 常用对计算得到的谐振频率乘一个校正因子, 再用校正后的频率来计算零点振动能和不同温度下的热力学性质. Johnson III等[53]给出了不同基组和不同理论级别下的频率校正因子. 此外, 一维受阻内转动是处理有机化合物中极为常见的方法. 分子单键内转动势能面上有多个最小值, 不能通过用对谐振子势能函数的微扰处理来描述, 因此通常用受阻内转子模型来处理这些内转动模式[54]. 由于内转动模式的振动频率较低, 对零点振动能和0 K下的热力学数据影响较小; 但在高温下, 受阻内转动对热力学参数有显著的影响, 特别是对熵和热容的影响较大[55]. Li等[52]研究表明, 与实验结果相比, 考虑受阻内转动后, 所得C5~C8烷烃的热容的平均绝对误差由10.75 J·mol‒1·K‒1降到2.85 J·mol‒1·K‒1. Vansteenkiste等[56]研究了乙烷到正辛烷的一系列烷烃的熵和热容, 结果显示, 熵和热容的误差随体系的增大而变大, 谐振子近似下, 高碳烷烃熵和热容的标准偏差接近10%, 而经受阻内转动修正后, 其标准偏差可降到低于1%. 这些结果表明, 考虑受阻内转动对高温下的热力学参数的精确计算非常重要.
1,3-丁二烯是高碳烃热解和氧化的重要中间体, 其氧化动力学对于层级构建碳氢化合物燃烧反应的动力学机理非常重要. 此外, 1,3-丁二烯还是通过“C2+C4”苯生成烟尘和多环芳烃(PAH)的重要中间体. 同时, 1,3-丁二烯也是一种危险的致癌物质, 会通过烟草烟雾、 森林火灾、 汽车尾气和汽油蒸发排放物等排放到大气中. 因此, 更好地了解1,3-丁二烯的燃烧反应机理, 也有助于研究碳氢化合物的燃烧过程、 煤烟形成和有毒排放过程[57~60].
Curran课题组[58]开发的AramcoMech3.0机理能够可靠地描述宽范围条件下, 包括氢气、 一氧化碳、 甲烷、 甲醛、 甲醇、 乙炔、 乙烯、 乙烷、 丙烯、 异丁烯和1,3-丁二烯等C0~C4燃料的燃烧反应, 这个机理采用基团加和法计算了1,3-丁二烯燃烧所涉及物种的热化学性质. 此外, 该机理对每个物种都给出了SMILE式, 便于对机理中的物种进行电子结构和热力学数据计算. 本课题组[61]对AramcoMech3.0机理进行简化, 得到1,3-丁二烯的框架简化机理. 简化的1,3-丁二烯机理包含102个物种和586步反应, 能够可靠描述点火延迟时间、 射流搅拌反应器(Jet Stirred Reactor)中的物种浓度以及层流火焰速度. 简化机理中包含的物种数目和尺寸较小, 相对容易开展高精度电子结构方法的计算. 本文采用G4方法, 计算了1,3-丁二烯简化机理中102个物种的热力学数据, 考察了振动非谐性、 频率校正因子和受阻内转动对热力学数据的影响, 通过与文献报道的高精度热力学数据理论值以及ATcT, CCCBDB-NIST和NIST-JANAF数据库中的数据进行比较, 考察所得热力学数据的可靠性, 进一步研究了所得热力学数据对1,3-丁二烯的绝热燃烧温度和点火延迟时间的影响, 并考察了对这些燃烧特性有重要影响的物种.
1 计算方法
基于G4方法的结果, 采用VPT2计算非谐振动频率, 或者用Johnson III推荐的频率校正因子, 并考虑受阻内转动, 计算了1,3-丁二烯燃烧机理中102个物种在0~3000 K温度下的热力学数据. 在G4理论[40,62]中, 几何构型和谐振频率均在B3LYP/6-31G(2,)水平下得到, 计算零点振动能校正和热力学数据时的频率校正因子为0.9854. G4总能量的表达式中, 考虑了旋轨耦合修正的能量、 高阶能量修正和零点振动能. 还采用了Johnson III推荐的B3LYP/6-31G(2,)水平上的频率校正因子(0.9652), 结合G4给出的几何结构和电子能量, 重新计算了不同温度下的各物种的热力学数据. 此外, 在B3LYP/6-31G(2,)水平上, 用VPT2得到这些体系的非谐振动频率, 用以计算零点能以及热力学数据. 在VPT2计算中, 某些振动模式给出的非谐振动频率为虚频, 对于这类振动模式, 采用G4方法得到的频率计算热力学数据. 此外, 对于受阻内转动, 在B3LYP/6-31G(2,)水平上, 以间隔为10°的柔性扫描相关二面角, 得到受阻内转动的势能面, 用于计算热力学数据. 在柔性扫描得到的势能面上, 可能出现多个能量极小值点, 并对应不同的构象. 通过采用受阻内转动模型, 可以考虑这些构象对配分函数和热力学数据的贡献. 但是, 有一些构象需要同时扫描两个或者多个二面角才能得到, 因本文所采用的方法无法计算这类构象对配分函数以及热力学数据的贡献, 采用了如MSTor等[63]的方法进行计算.
首先, 用原子化焓方法计算0 K下的生成焓, 用MESS程序[64]计算了102个物种的配分函数, 再用ThermP程序[65]得到了100~3000 K温度范围内的生成焓、 热容和熵, 进一步使用Chemkin-Pro中的Fitdat程序[66], 将热力学计算结果拟合成14参数的形式. 采用G4, G4(S), G4(VPT2), G4(HD), G4(HD,S)和G4(HD,VPT2)6种方法计算了热力学数据. 其中, G4(S)方法基于G4方法计算了所得的谐振频率, 再乘上频率校正因子(0.9652), 进一步计算热力学数据; G4(VPT2)方法结合G4方法得到了几何结构、 电子能量, 再用VPT2所得的非谐频率和非谐零点能计算热力学数据; G4(HD)方法在G4方法基础上, 对内转动采用受阻内转子模式得到的热力学数据; G4(HD,S)方法基于G4(S)方法, 结合受阻内转动模式得到热力学数据; G4(HD,VPT2)方法基于G4(VPT2)方法, 结合内转动势能进一步计算了热力学数据. 所有从头计算均使用Gaussian 16程序包[67]完成, 所有机理的模拟计算均采用Chemkin-Pro程序包.
2 结果与讨论
2.1 热力学数据
2.1.1频率结果由于振动频率直接影响分子的热力学数据, 首先考察了以下4种频率与实验振动频率之间的差别: (1) B3LYP/6-31G(2,)方法得到的谐振频率; (2) 谐振频率乘以频率校正因子0.9854得到的频率; (3) 谐振频率乘以频率校正因子0.9652得到的频率; (4) 通过VPT2基于B3LYP/6-31G(2,)水平得到的非谐频率. 以CCCBDB-NIST数据库所包含机理中的26个物种的实验基频为参考, 这4种方法所得频率的平均误差、 绝对平均误差、 绝对平均百分比误差、 最大误差和最大百分误差列于表1. 可见, 这4种方法得到的平均绝对百分比误差(MAPD)分别为3.82%, 2.57%, 1.92%和2.21%, 最大误差(MAX)分别是304.7, 239.5, 148.4和108.1 cm‒1; 最大百分误差(MPD)分别是7.30%, 5.80%, 3.60%和10.10%. 可以看出, 采用频率校正因子0.9652所得到的频率与实验基频的差别最小, 而采用VPT2方法的非谐振频率误差略小于采用频率校正因子0.9854所得频率的误差. 但是, VPT2非谐振计算需要计算能量的四阶导数, 对大体系的计算量很大, 因此采用频率校正因子0.9652估计基频振动频率是一种经济可靠的方法. 与基频振动频率相比, 谐振频率几乎总是偏大, 而采用频率校正因子或者用VPT2后, 能够减小所得振动频率的误差. 此外, 虽然谐振频率通常比基频振动频率更大, 但是对于CH3, CH3O2, C2H4, CHOCHO, C2H2, CH3CHO, C3H6, C2H3CHO, C4H6和C5H6这10个分子的某些振动模式而言, 谐振频率低于实验基频, 采用频率校正因子后得到的频率误差更大. 对于C2H2键角弯曲的振动模式, VPT2方法得到的基频振动频率甚至比谐振频率还大.

Table 1 Comparison of 26 molecular calculations and fundamental frequencies*
* diff RRHO-fund is the comparison of the harmonic with the fundamental frequencies; diff G4-fund is the comparison of the G4 scale factors for harmonic frequencies(0.9854) with the fundamental frequencies; diff S-fund is the comparison of the scale factors for harmonic frequencies(0.9652) with the fundamental frequencies; diff VPT2-fund is the comparison of the anharmonic frequencies with the fundamental frequencies; MD is the mean deviation; MAD is the average absolute deviation; MAPD is the average absolute percentage deviation; MAX is maximum deviation; MPD is maximum percentage deviation.
2.1.20和298.15 K的热力学数据ATcT数据库包含了1,3-丁二烯机理中54个物种在0和298.15 K下的生成焓, ANL0方法包含了机理中52个物种在0 K下的生成焓. 由于0 K下内转动对生成焓没有 影响, 因此, 表S1和表S2(见本文支持信息)只列出ATcT和ANL0中这些物种在0 K下的生成焓, 以及G4, G4(S)和G4(VPT2)方法计算所得生成焓分别与ATcT数据和ANL0结果的差别; 同时, 也列出了 6种方法计算得到的298.15 K下的生成焓与ATcT数据的差别, 以及本文计算结果与ATcT数据和ANL0结果的均方根误差(RMSE). 结果表明, 这些方法所得热力学数据的误差非常接近. 对于0 K下的生成焓, 与ATcT值相比, 这些方法的RMSE约为2.3 kJ/mol; 与ANL0的结果相比, 这些方法的RMSE值约3 kJ/mol. 对于298.15 K下的生成焓, 这些方法的RMSE值约为2.2 kJ/mol. 表明这6种方法得到的0和298.15 K下的生成焓均达到了化学精度.
ATcT和高精度的ANL0方法未给出燃烧模拟所需要的热容和熵. 而CCCBDB-NIST数据库包含了1,3-丁二烯机理中39个物种298.15 K下的热容和30个物种的标准熵(表S3和表S4, 见本文支持信息). 与CCCBDB-NIST数据库给出的298.15 K下的热容数据相比, 采用G4, G4(S), G4(VPT2), G4(HD), G4(HD,S)和G4(HD,VPT2)方法所得热容的RMSE分别为1.8, 1.9, 2.6, 1.3, 1.3和2.2 J·K‒1·mol‒1; 6种方法得到298.15 K下熵的RMSE分别为2.5, 2.5, 2.7, 1.9, 1.9和2.1 J·K‒1·mol‒1. 考虑内转动后, C2H5和CH3CO的热容误差分别降低了4.0和3.5 J·K‒1·mol‒1; H2O2和CH2OH的熵误差 分别降低了6.6和2.9 J·K‒1·mol‒1, 对于其它含有内转动的分子, 内转动对热容和熵的影响在1.0 J·K‒1·mol‒1以内. 可见, 考虑内转动比不考虑内转动, 采用相同方法所得热容和熵的RMSE均略有减小. 此外, G4和G4(S)方法所得熵的误差比G4(VPT2)的略小, 特别是C2H6和C2H2的熵, G4(VPT2)结果的误差比G4的误差分别大5.3和2.4 J·K‒1·mol‒1, 而对于机理中的其它分子, 用G4, G4(S)和G4(VPT2)3种方法计算所得到的热容和熵非常接近.
2.1.3100~3000 K的热力学数据前面仅比较了0和298.15 K温度下的热力学数据, 而燃烧模拟所需的是高温下的热力学数据, 目前, 在文献报道的高温下的热力学数据很少. NIST-JANAF数据库给出了一些物种在高温下的热力学数据, 包含了1,3-丁二烯机理中的16个物种的生成焓、 热容和熵, 其中, 只有H2O2分子有受阻内转动. 采用G4, G4(S), G4(VPT2), G4(HD), G4(HD,S)以及G4(HD,VPT2) 6种方法得到了这16个物种在100~3000 K温度下的生成焓、 热容及熵, 并与NIST-JANAF的热力学 数据进行了对比. 结果显示, 这6种方法得到的这16个物种的生成焓的平均均方根误差(MRMSE)为2.1 kJ/mol左右; 热容的MRMSE约为0.8 J·K‒1·mol‒1; 6种方法下熵的MRMSE分别为1.3, 1.0, 1.4, 1.1, 0.8和1.2 J·K‒1·mol‒1. 此外, 考虑内转动后, H2O2熵的RMSE比不考虑内转动的RMSE小 3 J·K‒1·mol‒1, C2H2用G4(VPT2)得到的熵, 比采用G4和G4(S)得到熵的RMSE大6 J·K‒1·mol‒1, 其生成焓和热容的误差比较接近. 对于其余的14个物种, 用这6种方法得到的生成焓、 热容和熵的RMSE均很接近.
2.1.46种方法热力学数据的比较为了考察频率校正因子、 非谐性以及受阻内转动对物种热力学性质的影响, 进一步比较了这6种方法所得102个物种在100~3000 K温度下的热力学数据之间的差异. 用这6种方法所得生成焓、 热容和熵之间的MRMSE列于表2. 首先考察频率校正因子和非谐性对热力学的影响. 与G4方法对比, G4(S)和G4(VPT2)得到的生成焓的MRMSE分别为1.5和1.4 kJ/mol, 热容的MRMSE均为0.8 J·K‒1·mol‒1, 熵的MRMSE分别为2.4和3.2 J·K‒1·mol‒1. 结果表明, 采用不同的频率校正因子或者采用VPT2计算非谐频率对生成焓、 热容和熵的影响不大. 另外, 进一步考察受阻内转动对生成焓、 热容和熵的影响. G4和G4(HD)所得生成焓的MRMSE为4.0 kJ/mol, 热容的MRMSE为3.1 J·K‒1·mol‒1, 熵的MRMSE为6.4 J·K‒1·mol‒1. G4(HD,S)与G4(S), G4(HD,VPT2)与G4(VPT2), G4(HD)和G4所得热力学数据之间的差别非常接近. 这些结果表明, 受阻内转动对生成焓、 热容和熵均有明显影响, 其中对熵影响最为显著. 此外, 内转动对机理中C2H3COCH2OOH, C2H3CHOHCH2OO和C4H6OHOOH1-4-3这3个物种的生成焓、 热容和熵影响最大. 进一步比较了G4(HD)方法计算的这3个物种在100~3000 K温度下的生成焓、 热容和熵与G4方法所得结果的差值. 结果显示, G4(HD)与G4得到的生成焓、 热容和熵之间的差值均随温度的升高先变大后变小. 对于C2H3COCH2OOH, G4(HD)的生成焓总是大于G4得到的生成焓; C2H3CHOHCH2OO和C4H6OHOOH1-4-3这2个物种在较低温度下, 采用G4(HD)所得的生成焓较大, 但是高温下G4的生成焓大于G4(HD)得到的结果; 两个方法得到3个物种生成焓的最大差别分别为22.2, ‒25.9 和16.7 kJ/mol. 对于热容, 这3个物种在低温下G4(HD)的热容大于G4得到的结果, 但是高温下G4的热容比G4(HD)得到的热容更大, G4(HD)和G4所得热容对这3个分子的最大差别分别为30.1, 18.8 和33.5 J·K‒1·mol‒1. 另外, G4(HD)得到的熵总是大于G4得到的熵, 对这3个分子, G4和G4(HD)得到熵的最大差别达到了34.7, 45.6和39.7 J·K‒1·mol‒1(图S1, 见本文支持信息).
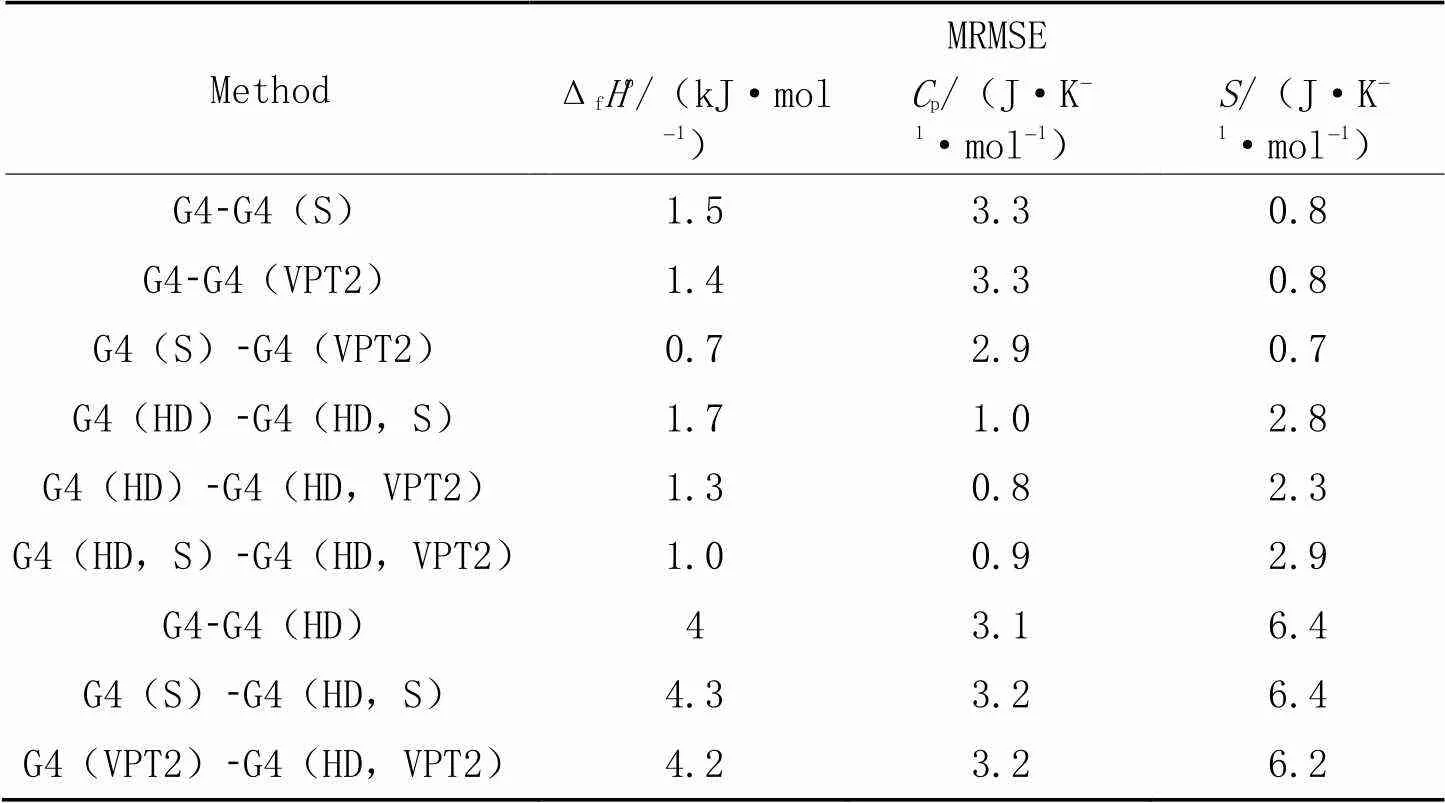
Table 2 Mean root mean square error(MRMSE) of enthalpy of formation, heat capacity and entropy for the six method species*
* G4-G4(S): Difference between G4 and G4(S) values; G4-G4(VPT2): difference between G4 and G4(VPT2) values; G4(S)-G4(VPT2): difference between G4(S) and G4(VPT2) values; G4(HD)-G4(HD,S): difference between G4(HD) and G4(HD,S) values; G4(HD)-G4(HD,VPT2): difference between G4(HD) and G4(HD,VPT2) values; G4-G4(HD): difference between G4 and G4(HD) values; G4(S)-G4(HD,S): difference between G4(S) and G4(HD,S) values; G4(VPT2)-G4(HD,VPT2): difference between G4(VPT2) and G4(HD,VPT2) values.
2.2 热力学数据对燃烧特性的影响
2.2.1绝热火焰温度绝热火焰温度是燃料燃烧的一个重要特性, 影响燃料绝热火焰温度的因素有很多, 除了燃料自身的物种外, 当量比、 初始温度、 初始压力和反应器的类型(恒压/恒容)等条件也会对绝热火焰温度有重要的影响. 需要指出的是, 在燃烧模拟中, 虽然压强会影响一些单分子反应和化学活化反应的速率常数, 但是模拟绝热火焰温度时, 只需热力学数据而无需动力学数据. 此外, 本文所构建的模型以及进行燃烧模拟时, 都采用了理想气体近似. 因此, 物种的热力学性质只依赖于温度, 不依赖于压强. 但是压强会通过影响化学平衡来影响绝热火焰温度. 图1(A)~(D)分别给出了等压绝热燃烧中, 初始温度分别为300和1000 K, 压力分别为1×105, 10×105和40×105Pa,当量比(, 燃料⁃氧气实际燃烧的质量比除以燃料⁃氧气燃烧的化学恰当质量比)为0.5~2.0条件下, 用这6套热力学数据以及原始机理热力学数据得到的1,3-丁二烯的绝热燃烧温度. 结果表明, 这6套热力学数据给出的绝热火焰温度之间最大差别均小于10 K; 但是用这6套热力学数据得到的绝热燃烧温度与原始机理热力学数据所得绝热火焰温度之间的最大误差达到42 K.
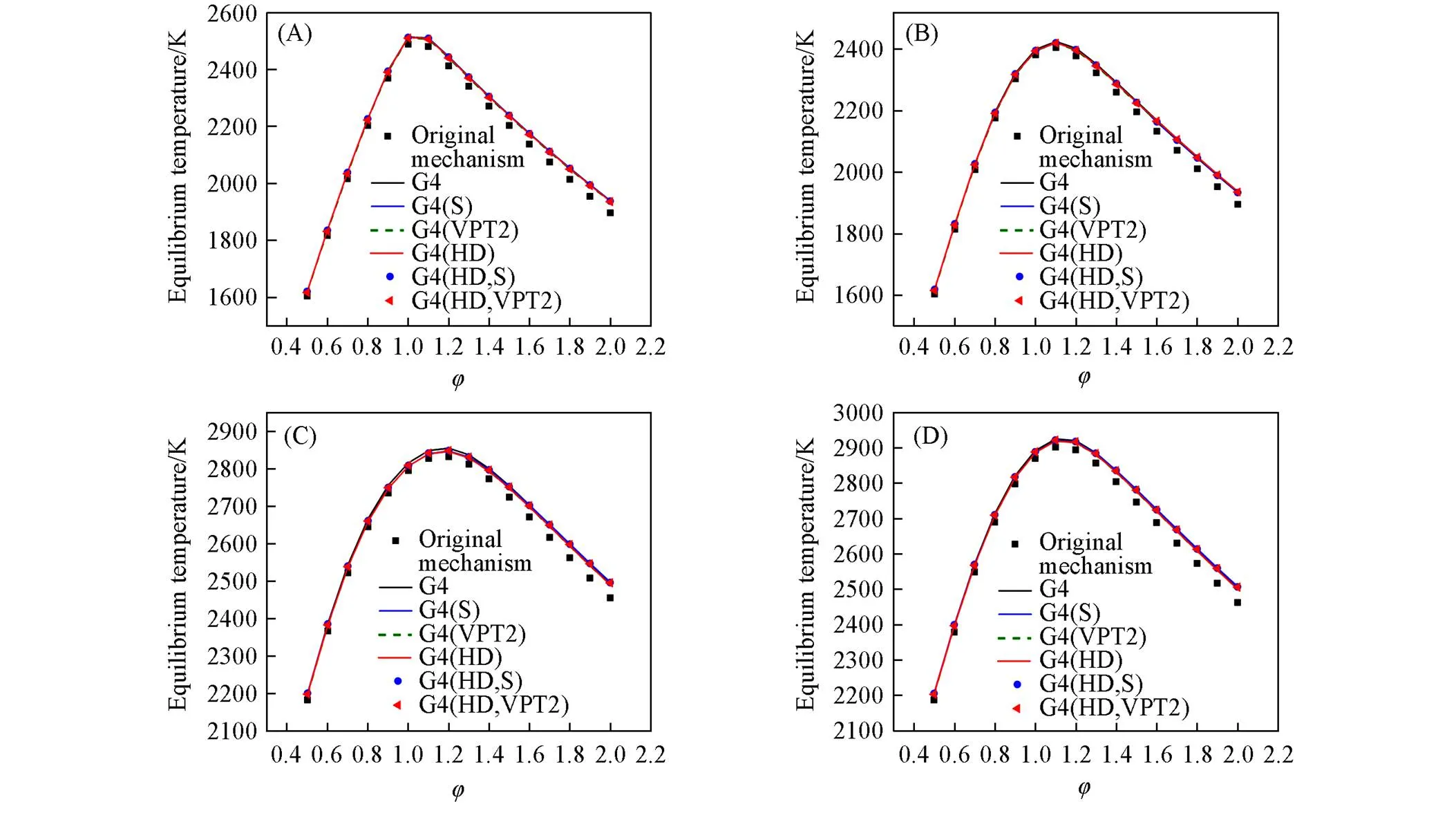
Fig.1 Adiabatic flame temperature for 1,3⁃butadiene in air at φ of 0.5—2.0
(A)=300 K,=40×105Pa; (B)=300 K,=1×105Pa; (C)=1000 K,=10×105Pa; (D)=1000 K,=40×105Pa.
绝热火焰温度主要依赖于反应物和产物的热力学数据, 首先考察了1,3-丁二烯的热力学数据对绝热火焰温度的影响. G4(HD)得到的1,3-丁二烯的生成焓与原始机理中的生成焓之间的RMSE为 0.9 kJ/mol, 热容的RMSE为4.2 J·K‒1·mol‒1, 熵的RMSE为1.8 J·K‒1·mol‒1. 这显示G4(HD)得到的1,3-丁二烯的热力学数据与原始机理中的热力学数据存在一定差别. 但是当将原始机理中1,3-丁二烯的热力学数据替换到G4(HD)的热力学数据中时, 所得绝热燃烧温度与G4(HD)热力学数据的结果差别约为6 K. 这个结果表明, 引起绝热火焰温度结果差异的不是1,3-丁二烯的热力学数据.
进一步将原始机理中的102个物种的热力学数据依次逐个替换到G4(HD)热力学数据中, 并模拟绝热火焰温度. 结果显示, 对绝热火焰温度影响较大的4个物种分别是CO2, CO, N2和O2, 替换它们的热力学数据对绝热火焰温度的最大变化分别是37, 28, 37和38 K, 而替换其它物种的热力学数据后, 绝热燃烧温度的变化均小于10 K. 采用G4(HD)得到的热力学数据, 将CO2, CO, N2和O2这4个物种的热力学数据用原始机理中的热力学数据替换后, 得到的绝热燃烧温度与用原始机理得到的绝热燃烧温度之间最大差别降低到9 K以内. 此外, 还进一步比较了100~3000 K温度下, 这4个分子的G4(HD)与原始机理之间, 以及原始机理与NIST-JANAF之间的生成焓、 热容和熵的RMSE. 与原始热力学数据相比, 这4个物种G4(HD)生成焓的RMSE均小于0.5 kJ/mol, 熵的RMSE的均小于0.8 J·K‒1·mol‒1, 热容的RMSE均小于0.5 J·K‒1·mol‒1. 与NIST-JANAF实验值相比, 这4个物种原始生成焓的RMSE均小 于0.1 kJ/mol, 热容的RMSE均小于0.5 J·K‒1·mol‒1, 熵的RMSE均小于0.1 J·K‒1·mol‒1. 可见, 虽然 G4(HD)得到的CO2, CO, N2和O2的热力学数据误差较小, 但是绝热燃烧温度对这几个物种的热力学数据非常敏感; 因此, 要得到可靠的模拟绝热火焰温度, 对这些小分子还是应该采用实验热力学数据.
2.2.2点火延迟时间点火延迟时间是反映燃料实际燃烧特性的重要物理量. 图2(A)~(D)分别给出了用1,3-丁二烯的简化机理分别结合G4, G4(S), G4(VPT2), G4(HD), G4(HD,S)和G4(HD,VPT2)这6套热力学数据以及原始机理的热力学数据, 在为0.5和2.0,为10×105和40×105Pa条件下, 得到的1,3-丁二烯机理的点火延迟时间. 结果显示, 与原始机理相比, 这6套热力学数据对1,3-丁二烯机理的点火延迟时间均显著偏大, 用G4和G4(S)热力学数据得到的点火延迟时间吻合很好, 而用G4(VPT2)热力学数据得到的点火延迟时间比G4和G4(S)的结果略小; 用G4(HD), G4(HD,S)和G4(HD,VPT2)这3套热力学数据得到的模拟结果差别很小, 但是比用不考虑内转动得到的热力学数据模拟结果偏大, 这是由于内转动对热力学数据有较大影响, 因此, 考虑了内转动的热力学数据与只考虑频率校正因子或者非谐性的热力学数据给出的点火延迟时间差别显著.
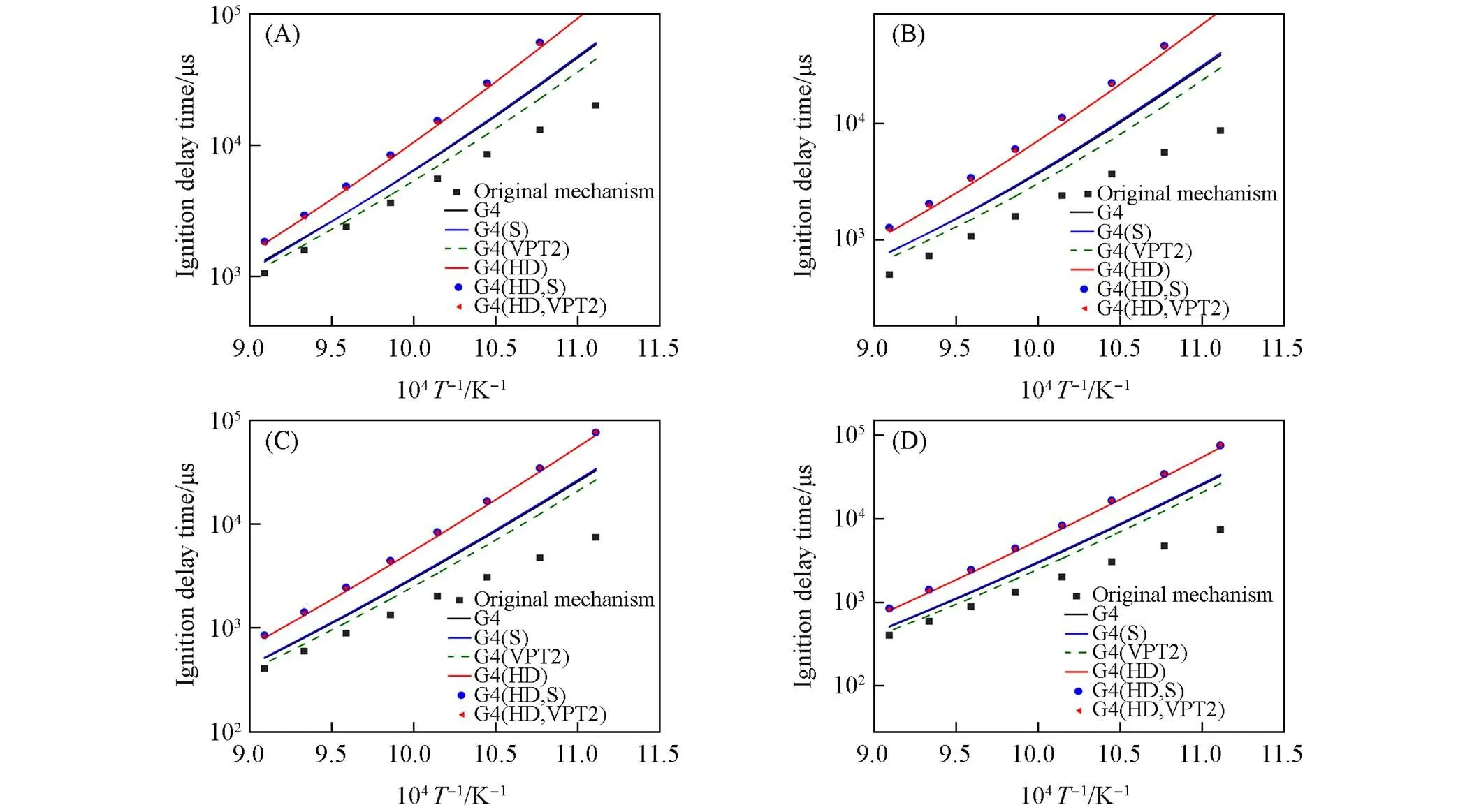
Fig.2 Ignition delay time measurements for 1,3⁃butadiene in air at six methods
(A)=0.5,=10×105Pa; (B)=2.0,=10×105Pa; (C)=0.5,=40×105Pa; (D)=2.0,=40×105Pa.
热力学数据对点火延迟时间的影响, 可能是由于它们对重要反应的逆反应速率常数的影响所致, 也可能是因为它们影响热量释放所导致. 为了考察热力学数据对点火延迟时间的影响, 基于原始的动力学机理, 将机理中所有可逆反应都拆分正反两个不可逆反应, 逆反应的速率常数通过正反应速率常数和原始机理中的热力学数据计算得到. 采用拆分后的机理结合不同的热力学数据, 模拟了各个条件下1,3-丁二烯的点火延迟时间. 结果显示, 无论使用哪套热力学数据, 拆分机理给出的点火延迟时间都和原始机理吻合得非常好. 这表明, 热力学数据是通过改变逆反应的速率常数来影响点火延迟时间的.
上述结果表明, 考虑内转动后, 得到的热力学数据更加可靠, 而且G4(HD), G4(HD,S)和 G4(HD,VPT2)这3套热力学数据之间的差别不大, 而且它们给出的点火延迟时间的结果也很接近. 基于G4(HD)的热力学数据, 进一步考察了热力学数据对点火延迟时间有显著影响的物种. 将原始机理中的102个物种的热力学数据依次逐个替换到G4(HD)热力学数据中, 在为1,为20×105Pa, 850 K条件下, 模拟了机理的点火延迟时间. 结果显示, 替换前后, 点火延迟时间差异最大的物种是 C4H63,1-3OH, 替换其热力学数据后, 得到的点火延迟时间相对误差达到91%. 以替换C4H63,1-3OH结果的G4(HD)热力学数据为基础, 进一步考察了其它101个物种分别采用原始机理热力学数据后, 对点火延迟时间的影响, 重复这个过程, 每次都以替换对点火时间影响最大的物种的热力学结果的 G4(HD)热力学数据为基础. 当将G4(HD)热力学数据中C4H63,1-3OH, C4H6O1-3OOH4, C3H4CH2OH-1OOH, C4H61-4OOH3, C3H5-A和C4H64,2-1OH这6个物种的热力学数据, 用原始机理中的热力学数据代替后, 再替换剩余96个物种中任一物种的热力学数据, 点火延迟时间的变化均小于10%. 将G4(HD)的热力学数据中这6个物种的热力学数据用原始机理的热力学数据替换后, 结果表明, 模拟得到的1,3-丁二烯的点火延迟时间与用原始机理热力学数据得到的结果差别均低于10%.
此外, 还对比了G4(HD)方法与原始机理在100~3000 K温度下生成焓、 热容和熵的差别, 结果显示, CH2CHCHCHO和C2H3COCH2OOH的热力学数据差别显著, 对生成焓、 热容和熵的RMSE分别为53.1和23.8 kJ/mol, 4.2和10.9 J·K‒1·mol‒1, 4.2和33.1 J·K‒1·mol‒1; 但是这两个物种的热力学数据对点火延迟时间影响较小. 对于点火延迟时间影响较大的6个物种, 其中, C4H63,1-3OH, C4H6O1-3OOH4和C3H4CH2OH-1OOH这3个物种的热力学数据差别较大, 其生成焓、 热容和熵的RMSE分别为28.5, 19.2和14.2 kJ/mol, 5.9, 13.8和8.8 J·K‒1·mol‒1, 19.2, 13.8和24.3 J·K‒1·mol‒1, 热力学数据对这些物种所参与反应的逆反应速率有较大的影响, 导致对点火延迟时间有显著的影响. C3H5-A, C4H61-4OOH3和C4H64,2-1OH这3个物种与原始机理的热力学数据差别较小, 其生成焓、 热容和熵的RMSE分别为9.6, 8.8和7.1 kJ/mol, 9.6, 8.8和7.1 J·K‒1·mol‒1, 5.9, 10.9和3.8 J·K‒1·mol‒1, 虽然这3个物种的热力学数据差别较小, 但是点火延迟时间对这些物种所参加反应的逆反应速率常数可能比较敏感.
综上所述, 本文基于G4方法, 分别考虑振动非谐性、 谐振频率校正因子和受阻内转动, 用6种方法计算了1,3-丁二烯热力学机理中102个物种在0~3000 K温度下的生成焓、 热容和熵. 结果表明, 与ATcT和ANL0结果相比, 这些方法得到的0和298.15 K温度下的生成焓误差都在4 kJ/mol以内, 与CCCBDB-NIST结果相比, 298.15 K的热容和标准熵的误差小于4 J·K‒1·mol‒1. 机理中16个小分子在100~3000 K温度下, 6种方法所计算的热力学数据与实验数据吻合得较好. 采用VPT2考虑非谐效应或者不同频率校正因子得到的热力学数据结果差别不大, 但是考虑内转动后对热力学数据有一定影响, 而且考虑内转动后得到的热力学数据与实验结果吻合得更好. 用所得热力学数据模拟得到的1,3-丁二烯的绝热燃烧温度以及点火延迟时间, 均与基于Aramco-Mech3.0得到的简化机理模拟结果差别较大. CO, CO2等小分子的热力学数据对于绝热燃烧温度影响显著, 虽然本文对这些小分子给出的热力学数据误差不大, 但是绝热燃烧温度对这些小分子的热力学数据非常敏感. 要得到可靠的绝热燃烧温度, 这些小分子的热力学数据应该采用实验值. 对于点火延迟时间, 用考虑内转动的热力学数据和不考虑内转动的热力学数据得到的点火延迟时间差别较大. 结果表明, 这些热力学数据主要是通过改变一些反应的逆反应速率常数来影响点火延迟时间. 进一步揭示了采用考虑内转动的G4热力学数据后, 对点火延迟时间有重要影响的物种. 研究结果为得到合理的热力学数据, 并结合化学反应动力学模拟, 可靠地预测火焰温度和点火特性提供了参考.
支持信息见http://www.cjcu.jlu.edu.cn/CN/10.7503/cjcu20220151.
[1] Lehn F. V., Cai L., Pitsch H.,., 2019,(1), 771—779
[2] Lehn F. V., Cai L., Pitsch H.,., 2020,, 394—408
[3] Lehn F. V., Cai L., Pitsch H.,., 2019,, 454—466
[4] Bugler J., Somers K. P., Silke E. J., Curran H. J.,, 2015,(28), 7510—7527
[5] Bugler J., Somers K. P., Silke M. J., Güthe F., Curran H. J.,, 2016,(36), 7192—7197
[6] Mathieu O., Petersen L. E.,., 2015,(3), 554—570
[7] Mohamed S. Y., Cai L., Khaled F., Banyon C., Wang Z., Rashidi M. A., Pitsch H., Curran H. J., Farooq A., Sarathy S. M.,, 2016,(14), 2201—2217
[8] Benson S. W.,, John Wiley and Sons, New York, 1976
[9] Ruscic B., Pinzon R. E., Morton M. L., Laszevski G. V., Bittner S. J., Nijsure S. G., Amin K. A., Minkoff M., Wagner A. F.,, 2004,(45), 9979—9997
[10] Ruscic B., Pinzon R. E., Laszewski G. V., Kodeboyina D., Burcat A., Leahy D., Montoya D., Wagner A. F.,, 2005.,(1), 6592—6601
[11] Johnson R.,, 2013,https://cccbdb.nist.gov/
[12] Chase M. W., Curnutt J. L., Mcdonald R. A., Syverud A. N.,, 1978,(3), 793—940
[13] Ruscic B., Pinzon R. E., Morton M. L., Srinivasan N. K., Su M. C., Sutherland J. W., Michael J. V.,, 2006,(21), 6592—6601
[14] Stevens W. R., Ruscic B., Baer T.,, 2010,(50), 13134—13145
[15] Ruscic B.,, 2013,(46), 11940—11953
[16] Goldsmith F. C., Magoon R. G., Green H. W.,, 2012,(36), 9033—9057
[17] Verevkin S. P., Emel"Yanenko V. N., Diky V., Muzny C. D., Chirico R. D., Frenkel M.,, 2013,(3), 805
[18] Burke S. M., Simmie J. M., Curran H. J.,., 2015,(1), 013101
[19] Martin J. M. L., Oliveira G. D.,., 1999,(5), 1843—1856
[20] Karton A., Daon S., Martin J. M. L.,., 2011,(4—6), 165—178
[21] Karton A., Martin J. M. L.,., 2021,(12), 124114
[22] Karton A., Rabinovich E., Martin J. M. L., Ruscic B.,., 2006,(14), 144108
[23] Tajti A., Szalay P. G., Csaszár A. G., Kállay M., Gauss J., Valeev E. F., Stanton J. F.,., 2004,(23), 11599—11613
[24] Harding M. E., Vázquez J., Ruscic B., Wilson A. K., Gauss J., Stanton J. F.,., 2008,(11), 114111
[25] Thorpe J. H., Lopez C.A., Nguyen T. L., Baraban J. H., Bross D. H., Ruscic B., Stanton J. F.,., 2019,(22), 224102
[26] East A. L. L., Allen W. D.,., 1993,, 4638
[27] Klippenstein S. J., East A., Allen W. D.,., 1996,(1), 118
[28] CsáSzár A. G., Allen W. D., Schaefer H. F.,., 1998,(23), 9751
[29] Tarczay G., CsáSzár A. G., Klopper W., Szalay V., Allen W. D., Schaefer H. F.,., 1999,(24), 11971
[30] CsáSzár A. G., Leininger M. L., Szalay V.,., 2003,(23), 10631
[31] Peterson K. A., Feller D., Dixon D. A.,., 2012,(1), 1—20
[32] Feller D., Peterson K. A., Dixon D. A.,., 2008,(20), 204105
[33] Feller D., Peterson K. A., Dixon D. A.,, 2010,(1), 613—623
[34] Feller D., Peterson K. A., Ruscic B.,., 2014,(1), 1407
[35] Klippenstein S. J., Harding L. B., Ruscic B.,, 2017,(35), 6580—6602
[36] Karton A.,., 2016,(3), 292—310
[37] Montgomery J. A., Frisch M. J., Ochterski J. W., Petersson G. A.,., 1999,(6), 2822
[38] Ochterski J. W., Petersson G. A., Montgomery J. A.,., 1996,(7), 2598
[39] Montgomery J. A., Frisch M. J., Ochterski J. W., Petersson G. A.,., 1999,(6), 2822—2827
[40] Curtiss L. A., Redfern P. C., Raghavachari K.,., 2007,(8), 124107
[41] Redfern P. C., Zapol P., Curtiss L. A., Raghavachari K.,., 2000,(24), 5850—5854
[42] Curtiss L. A., Raghavachari K., Redfern P. C., Rassolov V., Pople J. A.,., 1998,(18), 7764—7776
[43] Simmie J. M., Somers K. P.,, 2015,(28), 7235—7246
[44] Somers K. P., Simmie J. M.,, 2015,(33), 8922—8933
[45] Wilson B. R., DeYonker N. J., Wilson A. K.,, 2012,(25), 2032—2042
[46] Amos R. D., Handy N. C., Green W. H., Jayatilaka D., Palmieri P.,., 1991,, 8323
[47] Barone V.,., 2005,(1), 014108
[48] Barone V.,., 2004,(7), 3059—3065
[49] Barone V., Bloino J., Guido C. A., Lipparini F.,., 2010,, 157—161
[50] Truhlar D. G., Isaacson A. D.,., 1991,, 357—359
[51] Bloino J., Biczysko M., Barone V.,., 2012,(3), 1015
[52] Li Y. P., Bell A. T., Head⁃Gordon M.,., 2016,(6), 2861—2870
[53] Johnson III R. D., Irikura K. K., Kacker R. N., Kessel R.,., 2010,(9), 2822—2828
[54] Gao Y. G., He T. J., Li X. Y., You X. Q.,., 2019.(4), 1928—1936
[55] Ning H. B., Li Z. R., Li X. Y.,., 2016,(1), 23(甯红波, 李泽荣, 李象远. 物理化学学报, 2016,(1), 23)
[56] Vansteenkiste P., Van Speybroeck V., Marin G. B., Waroquier M.,, 2003,(17), 3139—3145
[57] Zhou C. W., Li Y., O’Connor E., Somers K. P., Thion S., Keesee C., Mathieu O., Petersen E. L., DeVerter T. A., Oehlschlaeger M. A., Kukkadapu G., Sung C. J., Alrefae M., Khaled F., Farooq A., Dirrenberger P., Glaude P. A., Battin-Leclerc F., Santner J., Ju Y., Held T., Haas F. M., Dryer F. L., Curran H. J.,., 2016,, 353—379
[58] Zhou C. W., Li Y., Burkea U., Banyona C., Somers K. P., Ding S., Khanc S., Hargis J. W., Sikes T., Mathieu O., Petersen E. L., AlAbbad M., Farooq A., Pan Y., Zhang Y., Huang Z., Lopez J., Loparo Z., Vasu S. S., Curran H. J.,., 2018,, 423—438
[59] Hansen N., Miller J. A., Kasper T., Kohse⁃HöInghaus K., Westmoreland P. R., Wang J., Cool T. A.,., 2009,, 623—630
[60] Vasu S. S., Zádor J., Davidson D. F., Hanson R. K., Golden D. M., Miller J. A.,, 2010,(32), 8312—8318
[61] Xue J., Xi S. H., Wang F.,., 2020,, 184—198
[62] Ye L. L, Wang D. Z., Bian H., Li B., Gao W., Bi M.,., 2021,,95—105
[63] Zheng J. J., Meana⁃Pañeda R., Truhlar D. G.,., 2013,(8), 2032—2033
[64] Georgievskii Y., Miller J. A., Burke M. P., Klippenstein S. J.,, 2013,(46), 12146—12154
[65] Keçeli M., Elliott S. N., Li Y. P., Johnson M. S., Carlo C., Yuri G., Green W. H., Matteo P., Wozniak J. M., Jasper A. W., Klippenstein S. J.,., 2019,, 363—371
[66]15092, Reacton Design, San Diego, 2009
[67] Frisch M. J., Trucks G. W., Schlegel H. B., Scuseria G. E., Robb M. A., Cheeseman J. R., Scalmani G., Barone V., Petersson G. A., Nakatsuji H., Li X., Caricato M., Marenich A. V., Bloino J., Janesko B. G., Gomperts R., Mennucci B., Hratchian H. P., Ortiz J. V., Izmaylov A. F., Sonnenberg J. L., Williams⁃Young D., Ding F., Lipparini F., Egidi F., Goings G., Peng B., Petrone A., Henderson T., Ranasinghe D., Zakrzewski V. G., Gao J., Rega N., Zheng G., Liang W., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Throssell K., Montgomery J. A. Jr., Peralta J. E., Ogliaro F., Bearpark M. J., Heyd J. J., Brothers E. N., Kudin K. N., Staroverov V. N., Keith T. A., Kobayashi R., Normand J., Raghavachari K., Rendell A. P., Burant J. C., Iyengar S. S., Tomasi J., Cossi M., Millam J. M., Klene M., Adamo C., Cammi R., Ochterski J. W., Martin R. L., Morokuma K., Farkas O., Foresman J. B., Fox D. J.,16,.1, Gaussian Inc., Wallingford CT, 2016
Effects of Thermodynamic Data on Combustion Characters of 1,3-Butadiene
RENNana1, XUEJie1, WANGZhifan2, YAOXiaoxia3, WANGFan1*
(,,610065,;,,611730,;,,610065,)
In this work, thermodynamic data for 102 species in a skeletal reaction mechanism for combustion of 1,3-butadiene were calculated based on the G4 method. Effects of anharmonic vibration, scaling factor for frequencies and internal rotations on these thermodynamic data of these species were investigated. The results show that effects of internal rotations are sizeable on thermodynamic data, while the anharmonic effect and different scaling factor for frequencies do not have a much effect on these thermodynamic data. Agreement between available experimental results and the present thermodynamic data will be improved when the internal rotations are considered. Effects of thermodynamic data obtained in this work on adiabatic combustion temperature and ignition delay time of 1,3-butadiene were also studied. The results indicate that experimental thermodynamic data for small molecules such as CO and CO2should be adopted to obtain reliable adiabatic combustion temperatures. On the other hand, ignition delay times with the original thermodynamic data diff considerably from those using thermodynamic data obtained in this work. The results indicate that effects of ignition delay times are affected by thermodynamic data through their effect on rate constants of reverse reactions. Furthermore, species whose thermodynamic data has large impact on ignition delay times are also identified. These works will be important in obtaining reliable thermodynamic data and kinetic mechanism for combustion.
Thermodynamic data; Anharmonicity; Frequency scale factor; Internal rotor; Combustion kinetic mechanism
O641
A
10.7503/cjcu20220151
2022-03-09
2022-04-25.
王 繁, 男, 博士, 教授, 主要从事量子化学和理论化学计算方法研究. E-mail: wangf@scu.edu.cn
国家自然科学基金(批准号: 21973063)资助.
Supported by the National Natural Science Foundation of China(No.21973063).
(Ed.: Y, K, S)

