错将必要当充要

石礼标

(江苏省淮安市清河中学,223001)

(A)[-40,-25] (B) [-40,0]

(C) [-25,25] (D) [-25,0]

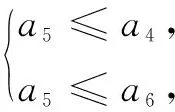
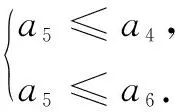
如果作为解答题,那此题又应该如何求解呢?

视角1通过函数的单调性研究数列的单调性

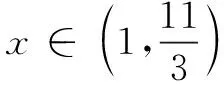
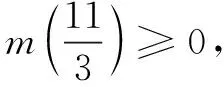
当m(1)≤0,即a≥-9时,m(x)在(1,+∞)必有一根x0,易知f(x)在(1,x0)单调减,在(x0,+∞)单调增,此时由a5是数列{an}的最小项,得a5≤a4,a5≤a6,a≥-9同时成立,解得-9≤a≤0.

综上,a的取值范围为[-25,0].故选D.

视角2利用必要条件解题

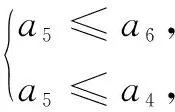
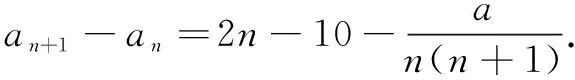
综上,选D.

评注解法2是利用必要条件得到-40≤a≤0后,在此基础上易得an在[5,+∞)单递增；再由a5前面只有有限的4项,只要逐一验证a5分别小于或等于前面4项即可.这种利用必要条件缩小a的范围后再求解,明显比解法1简单许多.

视角3转化为不等式恒成立问题

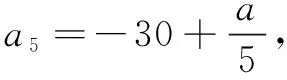
当n=5时,上式显然成立.

当n∈N*且1≤n≤4时,a必须满足a≥5n(n-6).而此时g(n)=5n(n-6)的最大值为-25(n=1时取得),所以a≥-25.

当n∈N*且n≥6时,a必须满足a≤5n(n-6).又此时g(n)=5n(n-6)的最小值为0(n=6时取得),所以a≤0.

综上,可得a∈[-25,0].故选D.

评注该解法将a5最小直接转化为an≥a5对n∈N*恒成立,用分离参数的方法转化为求相应函数在一定范围的最值问题,易理解且运算量也不大,这才是解决这类问题的最好方法!