一道双根式和的最值问题与变式拓展
2022-07-14 06:48:08杜海洋
高中数学教与学 2022年11期
杜海洋
(四川省成都经济技术开发区实验中学校,610100)
一、问题及解答
问题已知a,b,c为正实数,求
的最小值.
这是数学通讯2021年第8期上半月征解问题506,是一道双根式和的最值问题.笔者经过深入探究,给出其解法和变式拓展,供大家学习交流.

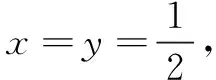
解法2由条件及柯西不等式和基本不等式,可得
等号当且仅当c=2b=4a时成立,故M的最小值为8.
二、变式拓展
变式1已知a,b,c为正实数,求
的最小值.
解由条件及基本不等式,可得

变式2已知a,b,c为正实数,求
的最小值.
解由条件及基本不等式,可得

变式3已知a,b,c为正实数,求
的最小值.
解由条件结合基本不等式,可得
≥5,
等号当且仅当b2=ac,a=4c时成立.故M的最小值为5.
变式4已知a,b,c为正实数,求
的最小值.
解由条件及柯西不等式和基本不等式,同原问题解法2可得

三、 推广
推广1已知a,b,c为正实数,则
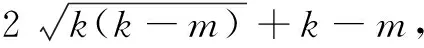
推广2已知a,b,c为正实数,则
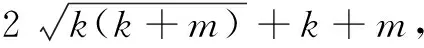
以上两个推广,有兴趣的读者可自行完成.
猜你喜欢
湘潮(上半月)(2023年6期)2023-08-11 04:06:32
湘潮(上半月)(2023年5期)2023-06-14 05:43:28
湘潮(上半月)(2023年3期)2023-06-14 05:35:36
湘潮(上半月)(2023年4期)2023-06-14 03:18:00
高师理科学刊(2020年2期)2020-11-26 06:01:26
语数外学习·高中版中旬(2020年2期)2020-09-10 07:22:44
河北理科教学研究(2020年1期)2020-07-24 08:14:34
中学生数理化·八年级数学人教版(2019年2期)2019-12-31 09:08:21
中学生数理化·中考版(2017年3期)2017-11-09 02:07:32
数理化解题研究(2017年4期)2017-05-04 04:07:54

