一道难题
2022-07-14 06:47:48单墫
高中数学教与学 2022年11期
单 墫
(南京师范大学数学科学学院,210023)
一位名叫李雨航的朋友问下面的问题有无好的解法:
问题已知正实数a,b,c满足

(1)

(2)
这道题的确不太容易.我请了几位朋友做,所提供的解法(包括李雨航提供的解),或者看不明白,或者怀疑有疏漏,没有看到我满意的.
哪位朋友有好的解法?
我也做了一个解,稍后提供(如有比我好的,我就藏拙了).
已有一种解法(见附页),这是计神的风格,一个式子就可解决问题.但怎么能想到?太复杂了,我连验证都头痛,但相信它是对的,谁有兴趣谁验证.仍欢迎其它解法,我的也将发表.又有一位网友发表精彩的解法.

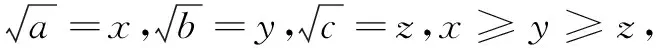

(2)若xyz<1,且x+y+z≤3,则注意到xy+yz+zx≥2+xyz⟺(xy+yz+zx)(x2+y2+z2)≥(2+xyz)(x2+y2+z2)=2(x2y2+y2z2+z2x2)+xyz(x2+y2+z2)⟺xy(x-y)2+yz(y-z)2+zx(z-x)2+xyz(x+y+z)≥xyz(x2+y2+z2),这等价于
①

≥x2+y2+z2-(x+y+z),
故① 式成立.
(3)若xyz<1,且x+y+z>3,则由x2+y2+z2=x2y2+y2z2+z2x2,知[(xy+yz+zx)+1]2=(x+y+z)2+2xyz(x+y+z)+1>10+6xyz>(xyz+3)2,开方即得证.
(后续)
猜你喜欢
作文周刊·小学一年级版(2024年28期)2024-07-14 15:50:23
作文周刊·小学一年级版(2023年28期)2023-07-12 06:51:24
作文周刊·小学一年级版(2023年4期)2023-01-20 03:34:20
作文周刊·小学一年级版(2022年36期)2022-07-06 05:59:40
今日农业(2021年16期)2021-11-26 06:05:34
江苏教育(2021年54期)2021-08-31 10:12:32
中学生数理化·七年级数学人教版(2018年3期)2018-05-30 06:58:14
法语学习(2016年3期)2016-04-16 21:45:33
中国卫生(2015年5期)2015-11-08 12:09:52
法语学习(2015年1期)2015-04-17 06:13:06

