例谈圆锥曲线综合试题的难点突破
杜银玲
(江苏省泰州市姜堰区娄庄中学,225506)
圆锥曲线是高中数学主干模块,是考查学生化归转化、运算求解等能力的主要载体,因此成为高考命题的重要内容,且常以压轴或把关题的形式出现.学生在解答问题时,由于对解题的思路方法不清楚、转化的方向不明确,简化的技巧不熟悉,常使解题事倍功半,甚至半途而废.本文举例说明此类问题分析、解答的思维过程,抛砖引玉,引导学生突破这一难点.
一、试题呈现

(1)求椭圆C的方程;
(2)设椭圆C的上、下顶点分别为A,B,过点(0,4)且斜率为k的直线与椭圆C交于M,N两点.求证:直线BM与AN的交点G在定直线上.

二、要点细析
1.明确求解通法,让解题轻车熟路
解圆锥曲线综合题的常用方法主要有线参法、点参法两种方法,它们的选择通常是根据题目中的动点类型来判断.若为“双动点型”,例如问题的背景是由一条斜率不确定的直线与椭圆相交,即有两个动点,常用线参法,即设直线斜率写出直线方程,再将直线与曲线方程联立,结合判别式、韦达定理求出两个动点坐标之间的关系.若为“单动点型”,即问题的不确定是由椭圆上的某一点引起的,此时可设出该点坐标,再结合条件建立与该点坐标相关的关系式,并利用点的坐标满足椭圆方程,进行消元处理.
本题的动点是直线与椭圆相交产生的,属于双动点型,因此可采用线参法.

①
2.明确结论与条件的关系,让解题方向清晰
(i)本题结论是证明直线BM与AN的交点G在定直线上,因此先写出直线BM与AN的方程,再联立方程组写出点G的坐标.
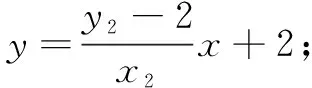
(ii)如何解这个方程组?是消x还是消y?大部分同学习惯于消y,致使解题陷入僵局.这就需要我们弄清一个问题,即点G在什么样的一条直线上?
在此,我们不妨取斜率对称的两条直线进行分析.如图1,当过点(0,4)的直线斜率为k(k>0)时,直线BM与AN的交点G在y轴的左侧;当斜率为-k时,点G在y轴的右侧,由椭圆的对称性可知点G在直线y=a(a为常数)上.
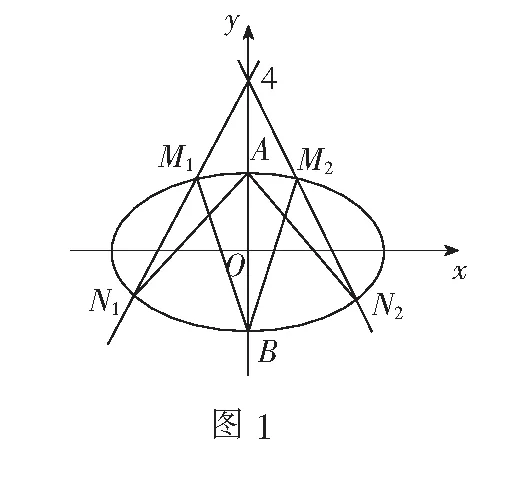
通过探究,我们已经清楚点G的纵坐标为常数,故解方程组要消去x,保留y,得
要得到y为常数,接下来再利用直线方程进行消元.将y1=kx1+4,y2=kx2+4代入上式,可得
②
3.明确转化策略,让解题柳暗花明
遇到② 式关于x1,x2不是对称式,此时① 式不能直接代入,需明确非对称式的几种常用转化策略.
策略1代入消元法
策略2降幂消元法
评注对非对称式的处理,除了上述两种方法外,某些问题也可以通过升幂的方式,结合根与系数的关系式进行转化.例如以下变式.
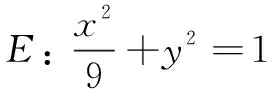
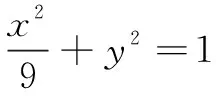
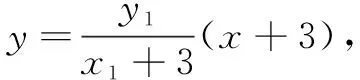
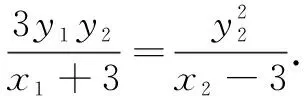

总之,圆锥曲线命题虽然形式变化多样、常考常新,但只要我们明确上述几个解题要点,便可以不变应万变.

