对一道椭圆四点共圆问题的探究

孟伟业

(江苏省扬州大学附属中学,225002)

前苏联数学家奥加涅相说:“必须重视,很多习题潜藏着进一步扩展其数学功能与教育功能的可行性.” 我市2020届高三5月份模拟考试第18题是一道涉及最值、定值的解析几何题,就是这样的一道好题.笔者对此从解法探究、试题背景、迁移举例三个方面进行了思考,使问题在探究中呈现更多的精彩.

一、试题呈现

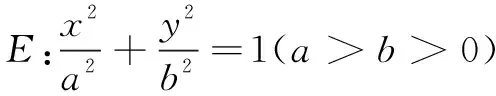
(1) 求椭圆E的标准方程;

(2) 求线段CD长的最大值;

二、解法探究

如下的解法1是命题组提供的参考答案.

3x2+4tx+2t2-2=0.

①

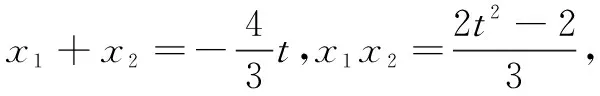
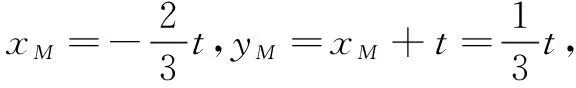
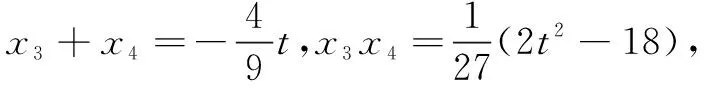
评注第(2)问通过联立方程组及利用弦长公式将弦CD的长表示为t的函数关系式,可求出最值;第(3)问的得分率较低,解答需在侧重坐标运算的同时关注整体结构,才能使问题顺利解决.若在解题教学中仅按参考答案去讲解,对学生无疑是“入宝山而空返”.我们应该多些追问,比如学生“卡壳”之处在哪里?能一题多解吗?本题有何背景?还能有何变式?如此等等.没有了这些追问,就难以体会到问题的活力与价值.

通过分析学生的解题过程,发现“卡壳”之处主要有:

下面给出这一转化的详解.

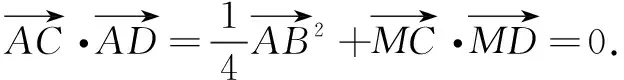
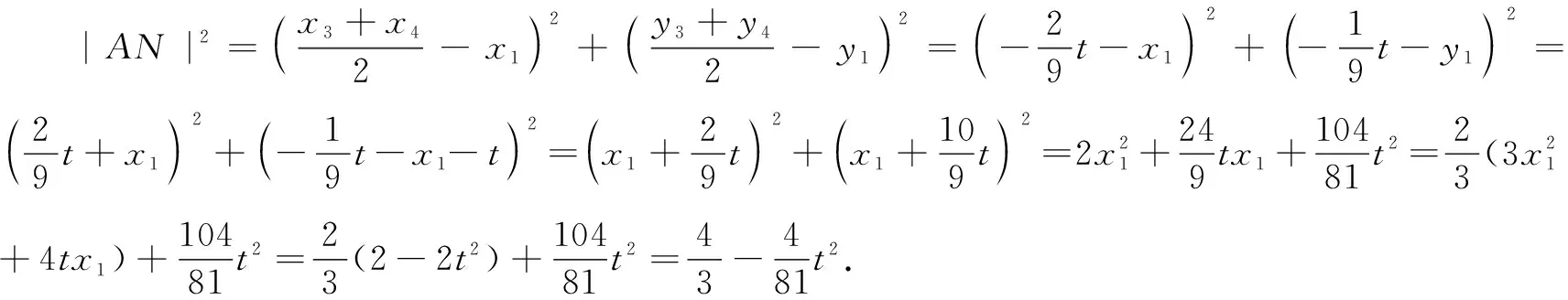
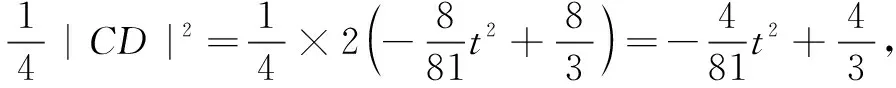
通过前面的计算我们可得到AC⊥AD,由图形的对称性易知BC⊥BD,所以点A,B,C,D均在以线段CD为直径的圆上.为此,参考文[1]给出如下的解法.

②

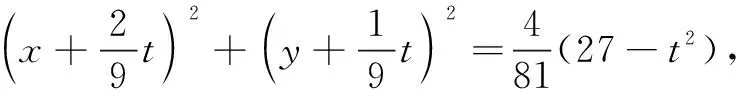
三、追根溯源

结合文[1],可知这道模拟题的命题背景正是椭圆中的四点共圆定理,在此我们仅给出文[2]中相应的结论.

根据上述背景,对直线AB,CD及椭圆E作一般化的推广,可得下列迁移的结论.

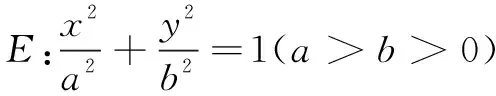
(1)|MA||MB|=|MC||MD|;

(2)若直线BC,AD的斜率存在,则kBC+kAD=0.

提示由kAB与kCD互为相反数,根据四点共圆定理得A,B,C,D四点共圆,再由相交弦定理即可得|MA||MB|=|MC||MD|;反之,由A,B,C,D四点共圆,根据四点共圆定理,得斜率存在时kBC+kAD=0.

类似地,我们也可以将这里的结论推广到双曲线、抛物线.下面仅给出双曲线和抛物线中的两道相关的试题,供大家练习.

(1) 求C的方程;

练习2已知直线l:y=x+m交抛物线C:y2=4x于A,B两点.

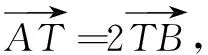
(2) 若点M,N在抛物线C上,且关于直线l对称,求证:A,B,M,N四点共圆.