刍议课本习题的有效利用*
黄小燕 刘祥云
(江苏省兴化中学,225700)
课本上的习题是专家从题海中精心挑选出来的,题目本身具有丰富的内涵和广阔的外延,如果仅仅是将习题匆匆做一遍,习题的效用会大打折扣,同时也失去了进行更深层次的探究的机会,所以有效利用课本习题是当前高考复习减负增效,摆脱题海的重要渠道.笔者以2019年人教版《数学》(必修二)第39页第3题为例,从问题的解法、问题背景、高考链接、性质探究四个角度谈谈课本习题效用的利用.

一、一题多解,拓展思维
解法1几何法

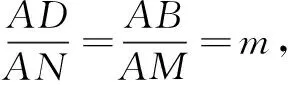
解法2坐标法
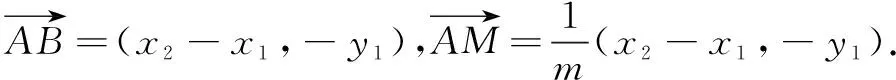

解法3基底法


解法4投影向量法
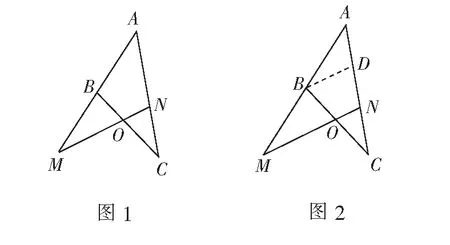
如图3,过点A作线段MN延长线的垂线,垂足为D,分别过点B,C作BB′⊥AD,CC′⊥AD,垂足分别为B′,C′.


评注一题多解可以加强对知识点的认识,增强与相关知识建立有效联系的方法和技能,将解决问题的角度提升到思想的层面.几何关系、坐标、基底、投影向量是向量问题中常见的四种解决方式,通过它们建立知识点之间的关联,实现了从数到形、由形到数的有效联系途径,有助于学生开拓视野、拓展能力.
二、归纳总结,升华认知



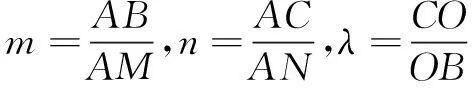
三、真题探寻,理解运用
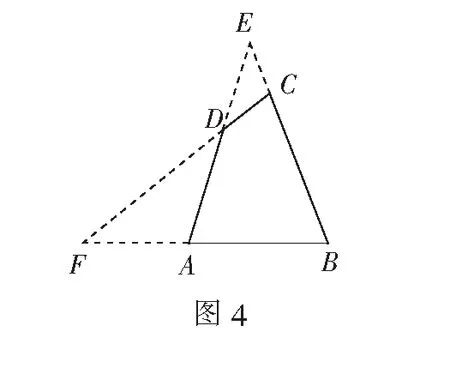
例1(2015年全国高考题)在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是______.

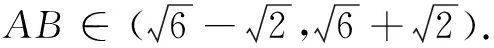

(1)求E的方程;
(2)证明:直线CD过定点.
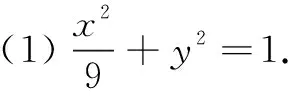
(2)由椭圆的对称性可知直线CD经过的定点必在x轴上.不妨设定点为Q,设点C(3cosα,sinα),D(3cosβ,sinβ).

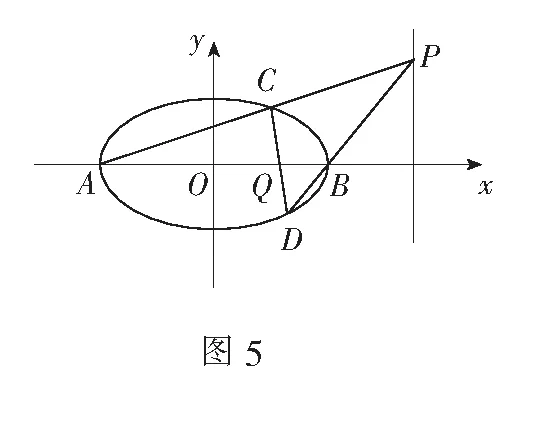
评注本题图5把完全四边形作为基本图形隐藏在解三角形问题和解析几何问题中.本解法表明利用梅涅劳斯定理解题是一个全新的途径,实现了从课本习题到高考真题的飞跃.这也提示我们在研究课本习题时要注重对基本图形的认识,对基本图形要进行深层次的探究.
四、探究性质,提升素养


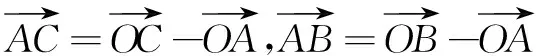

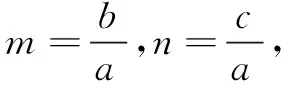
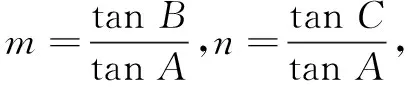
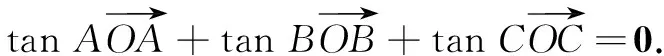

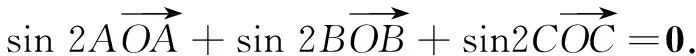
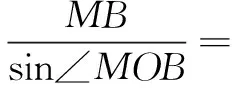


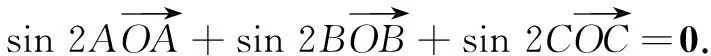
评注本题中推出的四个结论就是三角形“四心”的向量关系式,完全四边形中向量的形式就是三角形“四心”的统一形式,由此实现了从一般到特殊的探究过程.
数学建模活动与数学探究活动是新课标中四个主题之一,而课本习题是进行数学探究活动的重要素材,利用好典型的例题和习题,根据题目的背景和内涵进行数学探究,进而提升学习数学的能力和兴趣,对素养提升有很大的帮助.
——记我的原创感悟

