由教材案例谈数学建模能力的培养*

颜美玲

(浙江省杭州外国语学校，310023)

一、问题的提出

近年来,作为我国高中数学课程的六大核心素养之一的数学建模越来越受到重视.新的课程标准也首次将数学建模活动与数学探究活动纳入必修课程,并安排了具体的课时.有专家学者基于大样本的测试数据发现,我国学生的数学建模素养在六个数学核心素养中的测试平均分是最低的[1].

数学建模是应用数学解决实际问题的基本手段,也是推动数学发展的动力[2].这里所说的实际问题既包含现实世界中的实际问题,也包含数学内部的实际问题.很多一线教师正在积极探讨如何进行数学建模的课堂教学设计以及如何开展数学建模课堂教学等问题[3][4],读后受益匪浅.与此同时,笔者也开始思考:除了主题式的数学建模教学,教材中有没有值得我们一线教师好好开发利用的素材呢?本文以人教版《数学》必修第一册P227中的例10——“扇形内接矩形的面积问题”为例,与同行们共同探讨如何利用教材例题培养学生的数学建模能力.

二、原题及教材用意分析

该例题在教材中呈现如下:

教材在第五章三角函数中的“简单的恒等变换”第2课时中设置了如上例题.笔者觉得教材在此处设置该问题有两个用意:一是在例9的基础上,再通过具体的几何问题让学生掌握将形如y=asinx+bcosx的函数化为y=Asin(x+φ)的形式,进而求出最值等性质的方法;二是促进学生对函数模型多样性的理解,特别是让学生感受以角为自变量的优点,为后续三角函数的应用做好适当的铺垫和准备.

三、教学片断

1.原题的重新设计

师:关于最值问题,我们一般的解决方法和路径是怎样的?

生1:选择合适的自变量,求出其取值范围,建立函数模型求出最值.

设计意图笔者没有将教材中的例10直接呈现给学生,而是先作一定的改动,即将条件中的“记∠POC=α”去掉,并且将设问改成了“求矩形ABCD的最大面积.”主要目的是想通过开放性的探究方式让学生能自主地选择自变量建立函数关系,这样的设置比直接告诉学生设“∠POC=α”更能促进他们对函数模型多样性的理解.另外,在问题呈现后就让学生思考解决最值问题的一般方法,是希望学生能形成考虑一类数学问题的一般路径.

2.探究环节1(建立模型)

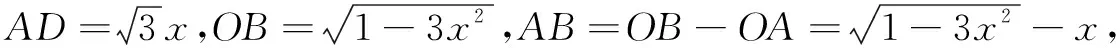
笔者并没有急着去评价上述两种解法,也没有急着去引导学生如何求上述两个函数的最大值,而是暂且将问题搁置,先让其他同学发表不同的解法,最后希望学生通过后续的探究自主解决上述问题.

师:还有没有其它的方法呢?

此时有一位学生举手了.

师:刚才三位同学选取三种不同的自变量建立函数关系,再考虑其最值问题.大家在此过程中有什么体会与感想呢?

众生:选取不同的自变量可以建立不同的函数.但此问题中,以角为自变量建立的函数求最值问题具有明显的优点,比较容易求.

此时又有另一个学生举手了.

设计分析由于个体差异及解题习惯的不同,加上学生在本节课之前还没有真正经历以角为自变量建立三角函数模型求解几何最值问题的过程,因此笔者在此处设置成开放式探究的形式,并让他们充分表达自己的想法和见解.从课堂反映来看,果不其然,在笔者巡视的过程中发现只有极少数的同学设角为自变量,绝大部分同学都采用了解法1或解法2.

3.探究环节2(模型求解)

既然有不少学生采用了解法1和解法2,笔者觉得有必要探讨如何求这两种解法得出的函数的最大值.这也是他们非常期待和关心的问题.

师: (引导)我们接着来求解法1中的函数S的最大值.大家能否从解法3中获得启发?

师:那么该如何求解法2中S的最值呢?

接着师生对含有二次根式的函数共同小结,可用三角换元进行转化,再通过一系列的恒等变形将其转化为y=Asin(ωx+φ)+k(或y=Acos(ωx+φ)+k)的形式,最后结合自变量的取值范围求出其最值.

设计意图虽然上述三种解法建立的函数模型不尽相同,但我们可以通过换元将函数类型进行转化.通过这样的探究过程可让学生体会到函数模型之间并不是割裂的,是可以互相转化的.当然,对于此问题来说,直接设角为自变量,会更方便更直接.

4.探究环节3(意外的探究)

解法3是教材例10给出的解法.但并不是所有的学生都是按此步骤求面积的最大值.当学生4讲完解法3后就有学生举手了,以下是她的想法.

看其他同学也是这样的反应!笔者继续引导.

经过几分钟的思考,不少同学解决了该问题.

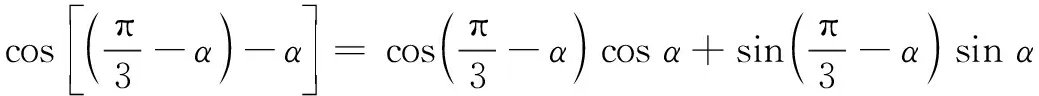
师:上述方法和解法3看似不同,它们有什么共同之处吗?

生10:都是通过恒等变形将有关三角函数式转化为形如y=Asin(ωx+φ)或y=Acos(ωx+φ)的形式,所以本质上是一致的.

师:大家认同吗?

生(全体):是的.我们可通过考虑y=Asin(ωx+φ)或y=Acos(ωx+φ)的最值及其它性质得到原来函数的最值及其它性质了.

5.探究环节4(拓展探究)

生11:将问题一般化:对任意角α,β,类似推导可得恒等式

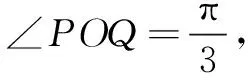
师:既然如此,我们是否可以有更进一步的猜想呢?

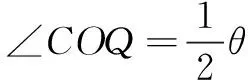
师:非常好!请大家课后继续探究并完成证明.

设计意图新教材将“和差化积,积化和差”公式作为三角恒等变换的应用简单提出,虽然公式已不要求学生掌握,但需要让学生感知其中蕴含的思想方法.生8提出的疑惑恰好可以非常自然地推导出上述这两个公式,可谓一举两得.另外,将∠POQ一般化,虽然解的过程基本类似,但对学生来说还是有一定困难的,考虑课堂时间有限,所以笔者将此猜想的证明放到了课后,希望一些学有余力的学生自主探究完成.