一道圆锥曲线非对称问题的多角度思考

谭 辉

(广东省佛冈县佛冈中学, 511600)

一、概述

圆锥曲线作为高考必考核心内容之一,笔者在授课过程中发现,学生遇到圆锥曲线非对称结构问题时,往往觉得无从入手,很多时候便直接放弃,十分可惜.此类问题往往涉及多个知识点的汇合,具有一定的综合性及难度,对数学运算、逻辑推理等能力要求较高.教学时,教师应结合“深度学习”的理论要求,把握解题的基本方法,引导学生逐层深入、积累模型,最终找到解决问题的本质.笔者通过对一道圆锥曲线非对称结构问题的多角度切入求解,给出其适当的拓展与变式,以寻求探究圆锥曲线非对称结构问题的一般性解决方法.

二、问题呈现

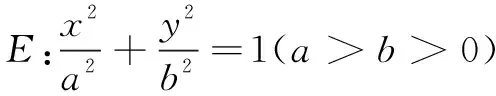
(1)求椭圆E的方程;

(2)设过点F2的直线l与E交于A,B两点,点M(0,1),且∆MAF2的面积为∆MBF2面积的2倍,求直线l的方程.

评注代数式y1=-2y2为非对称结构,需要通过适当的处理使之变为对称结构,下面就以此为例,给出此类y1=λy2(或x1=λx2)问题的几种处理方法,并对其进行拓展.

三、解法探究

策略1倒数求和法

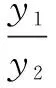
策略2配凑法

由y1+λy2=0配凑,得λ(y1+y2)=(λ-1)y1,y1+y2=(1-λ)y2,两式相乘,可得λ(y1+y2)2=-(λ-1)2y1y2,从而问题转化为对称结构.

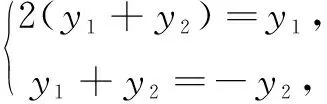
策略3方程组法

该策略的实质是借助方程思想,由非对称式结合韦达定理,列方程组解答.

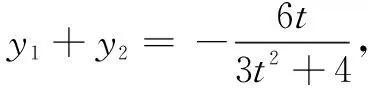
四、方法拓展

(1)求椭圆C的方程;

(2)过椭圆C的右焦点F的直线l与椭圆C交于M,N两点,O为坐标原点,若S∆OMF∶S∆ONF=3:1,求直线l的方程.

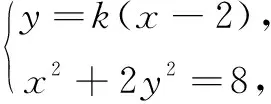
评注代数式3x2+x1=8为非对称结构,可借鉴例1的方法进行处理,进而得到形如ax1+bx2+c=0(或ay1+by2+c=0)的一般性处理方法.

策略1倒数求和法

结合韦达定理,化简可得k2=1.所以直线的l方程为x±y-2=0.

策略2配凑法

由x1+λx2=c配凑,得

两式相乘即可转化为对称结构.

策略3方程组法

五、变式研究

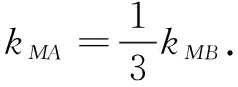
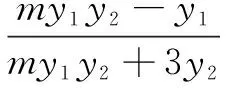
六、结束语

核心素养视角下的数学教学,要求教师在教学过程中除了使学生掌握好知识与技能外,还要引导学生体会到数学知识的本质,促进学生数学核心素养的提升.对于圆锥曲线中非对称结构问题,作为高考题的一个难点问题,笔者牢牢抓住把“非对称结构”转化为“对称结构”这条主线,通过多种方法比较,来启发学生以多角度、多层次去思考和体验解决问题的方法.因此,只要教师在教学过程中把握好问题的本质,创设合理的教学情境,通过恰当的例子和设问,启发和引导学生进行独立思考与合作探究,使学生积累好一定的解题模型,学会合理转化,相信学生定会掌握好这一知识难点.