小车位环境下的自动泊车路径规划与跟踪控制

冯欣阳，李春书，唐风敏

河北工业大学 机械工程学院，天津 300401

随着我国汽车保有量的增加，一些问题也随之显现，泊车可用空间的减小便是其中之一。狭小车位环境下的泊车需要丰富的驾驶经验及娴熟的驾驶技术，无形之中增加了驾驶人员的操作难度和操作体验。目前，智能车辆的自动泊车研究是许多研究者们关注的问题之一[1-3]。自动泊车包括环境感知、泊车控制、人机交互等技术。

泊车控制主要有两种方法：人工智能方法和运动状态规划及轨迹跟踪。人工智能方法通过智能算法使控制器在泊车过程中模拟驾驶员的操作行为[3]。文献[4-9]通过蚁群算法、神经网络、模糊控制等智能算法，实现泊车操作；由于实际泊车环境的复杂性，驾驶员需要面对不同的泊车环境做出不同反应，增加了人工智能方法的实现难度。一些研究者提出基于路径规划及路径跟踪的泊车控制方法[10-18]。研究者们对于泊车路径规划的研究大多采用曲线组合或多项式插值的方式[11-14]。此外，有些研究者也采用贝塞尔曲线、B样条曲线设计泊车路径[15-16]。路径跟踪采用滑模控制、自适应控制、模型预测控制等多种跟踪控制方法[12-18]。

上述泊车路径规划的研究均是针对一次泊入到位路径进行设计实现泊车的；若车位长度较小，不能实现一次泊入到位，车辆需要在车位内进行位姿调整。为方便描述，将需要在车位内进行位姿调整的车位称为小车位。目前，一些研究者已针对小车位环境自动泊车的路径规划进行研究。文献[19]通过建立预定义模态集，采用遍历策略，计算最优参数，对泊入段、调整段路径进行规划；但模态集的建立需要考虑多种情况，计算量较大。文献[20]通过B 样条曲线建立泊入路径及调整路径；该调整路径曲率连续，但是B样条曲线复杂程度高，求解过程较为困难。文献[21]根据车位长度及车辆当前航向角，通过多次揉库，实现狭小车位内的姿态调整；该方法耗时长、计算成本高。文献[22]通过三段式路径规划实现平行车位内的位姿调整；调整路径通过前进圆弧路段实现位姿调整，但该方法在换向时，曲率不连续且所需车位较大。文献[23]利用曲线组合设计了泊入路径和调整路径，采用相切圆弧实现车位内的倒车位姿调整，其调整路径存在曲率突变的不足。

为使泊车路径曲率连续无突变且计算方便，利用回旋曲线曲率连续的特点，将回旋曲线、直线、圆弧曲线组合设计形成平滑的泊入段路径和调整段路径；在非时间参考变量的前提下结合滑模控制原理，设计路径跟踪控制器，实现泊车路径的跟踪控制。

1 平行车位泊车路径规划

1.1 小车位环境及路径分析

当车辆侧向泊入平行车位时，停泊时的标准位姿通常如参考文献[24]所描述的状态，如图1所示。ab和dc分别代表车辆前端和后端；Lf、L、Lr、Wa分别代表前悬、轴距、后悬、车宽；Lp、Wp分别代表车位的长度与宽度；Db、Dr分别代表车辆后端、右端与车位障碍物边界之间的安全距离。

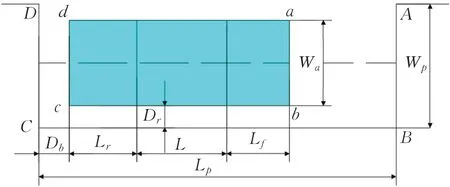
图1 车辆泊车位姿示意图Fig.1 Diagram of vehicle standard position and pose

如图2 所示，建立大地坐标系OXY，O为固定原点，障碍物边界点A与原点O重合，泊车初始位姿如图2 中I 位置所示，车辆的初始位置、初始航向角分别为C1、θ0，选择车辆后轴的中心点作为路径跟踪的参考点。

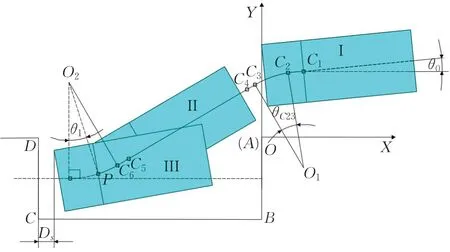
图2 小车位下的泊入路径Fig.2 Parking path under small parking space

泊入路径由回旋曲线C1-C2、圆弧曲线C2-C3、回旋曲线C3-C4、直线C4-C5、回旋曲线C5-C6、圆弧曲线C6-P组成；车辆的极限位置为图2中III位置所示。

调整路径由前进路段和后退路段组成，前进路段由回旋曲线P-P1、回旋曲线P1-P2、圆弧曲线P2-P3、回旋曲线P3-P4、回旋曲线P4-P5、圆弧曲线P5-P6、回旋曲线P6-P7组成；P-P1、P1-P2为两段反向回旋曲线，P3-P4、P4-P5为两段反向回旋曲线；后退路段由直线P7-P8组成；调整路径如图3所示。

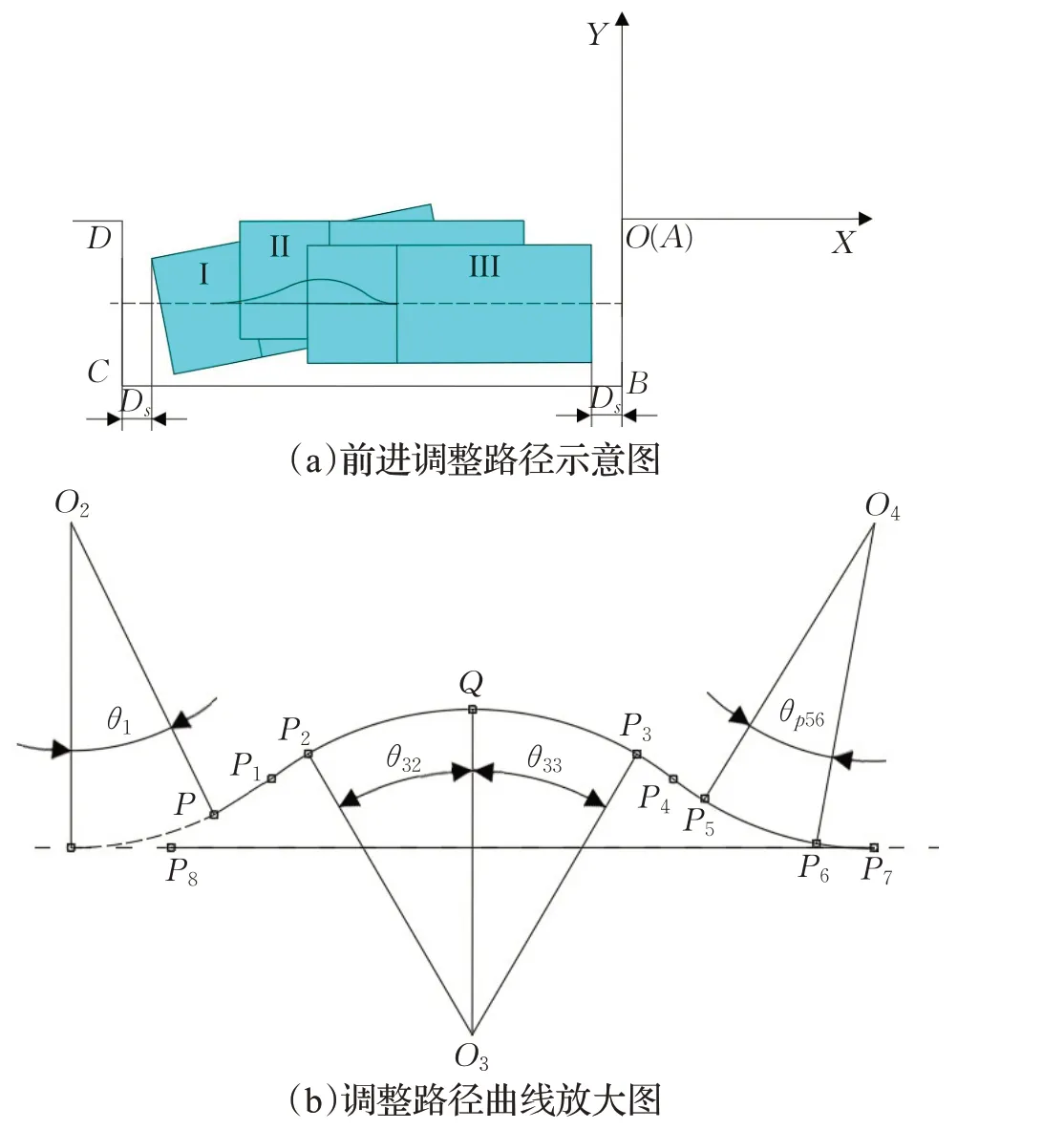
图3 小车位内调整路径Fig.3 Adjust path in small parking space

设Rmin为车辆最小转弯半径，泊车路径的最大曲率不超过ρmax=1Rmin；在泊车过程中为避免车身与障碍物发生碰撞，需要满足以下条件：（1）泊入阶段，车辆右前顶点b与A点不发生碰撞（记为Cons G）；车辆右侧bc与A点不发生碰撞。（2）调整阶段，车辆右前顶点b与车位BC边界不发生碰撞；车辆前端ab与车位AB边界的安全距离为Ds。

1.2 泊入路径的设计

设回旋曲线的曲率变化率为k，初始点为固定原点O，初始方位角为零，回旋曲线上曲率为ρ的i点坐标及方位角αi为：

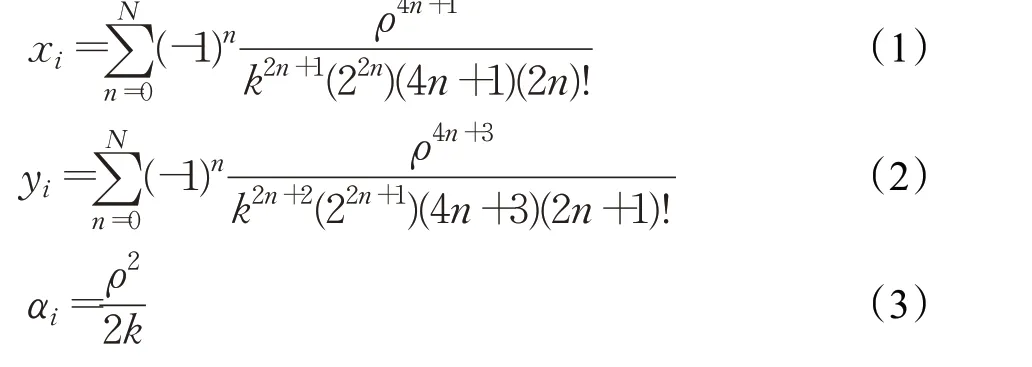
设圆弧曲线的半径为R，圆心角为θ，起始点为固定原点O，初始方位角为零，圆弧曲线上对应圆心角为θ的j点坐标为：

xj=Rsinθ（4）

yj=R(1-cosθ) （5）

回旋曲线C1-C2曲率变化率为kC12，C1-C2曲线构造原理如图4 所示，由式（1）、（2）得到初始回旋曲线O-C2*，C2*处的方位角为αC2*由式（3）求得，初始曲线如I所示。将曲线O-C2*逆时针旋转π+θ0，如位置II所示，沿向量OC1平移至O和C1重合，得到回旋曲线C1-C2，如位置III所示。

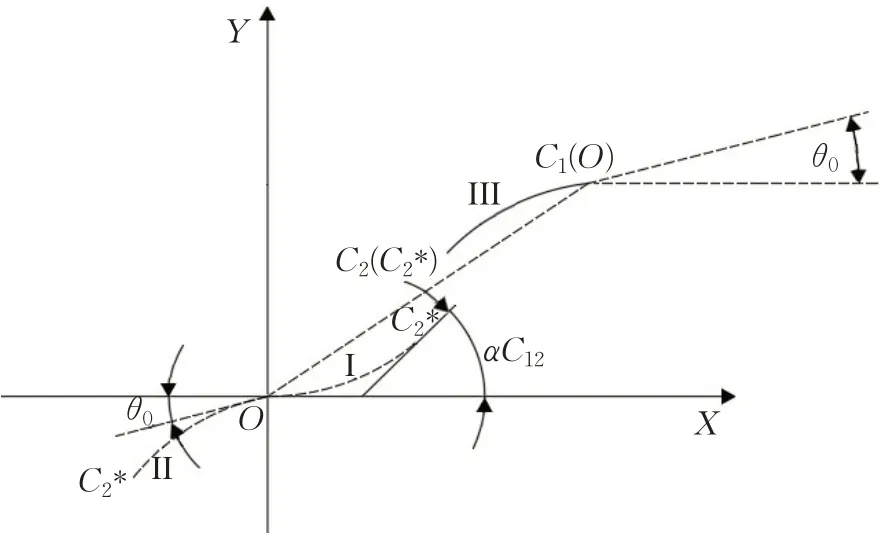
图4 C1-C2 曲线构造原理Fig.4 Construction principle of C1-C2 curve

圆弧曲线C2-C3的曲率为ρC23，圆心角为θC23，初始圆弧曲线O-C3*由式（4）和（5）求得，将其逆时针旋转αC2*+θ0+π，沿向量OC2平移至O与C2重合，得到圆弧曲线C2-C3，C3点处的方位角为αC3=θ0+αC2*+θC23。

同理，其余回旋曲线和圆弧曲线也类似求得。回旋曲线C3-C4的曲率变化率为kC34，初始回旋曲线为OC3′，C3′处的方位角为αC3′。设P点的方位角为θ1。圆弧曲线C6-P的曲率为ρC6P，圆心角为θC6P，初始圆弧曲线为O-C6*；回旋曲线C5-C6的曲率变化率为kC56，初始回旋曲线为O-C6′，C6′处的方位角为αC6′；连接C4、C5得到直线C4-C5。

上述圆弧曲线的半径均取Rmin，满足θ1+θC6P+αC6′=αC3+αC3′。

泊入运动中允许的最大车速vmax1=3 km/h，曲率变化率的最大值kmax1=wmax2，wmax代表前轮最大转向角速度。

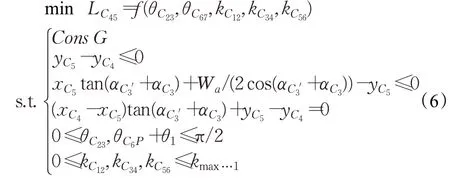
泊入路径中直线C4-C5长度LC45最小为优化目标，泊入路径规划转换为非线性规划：式中，第一个不等式表示车辆右前顶点b与A点不发生碰撞；第二个不等式为直线C4-C5存在性条件；第三个不等式表示车辆bc侧与A点不发生碰撞；第四个等式表示直线C4-C5分别与回旋曲线C5-C6、回旋曲线C3-C4曲线相切。

1.3 调整段路径设计

为了方便设计，将圆弧曲线P2-P3分为P2-Q和Q-P3两段圆弧，Q点切线水平，如图3（b）所示。

回旋曲线P6-P7的曲率变化率为kP67，初始回旋曲线为O-P6*，P6*处的方位角为αP6*；圆弧曲线P5-P6的曲率为ρP56，圆心角为θP56，初始圆弧曲线为O-P5*；回旋曲线P4-P5的曲率变化率为kP45，初始回旋曲线为O-P5′，P5′处的方位角为αP5′；回旋曲线P3-P4的曲率变化率为kp34，初始回旋曲线为O-P3*，P3*处的方位角为αP3*；圆弧曲线Q-P3的圆心角为θ33，曲率为ρQP3，初始圆弧曲线为O-P3′；回旋曲线P-P1的曲率变化率为kPP1，初始回旋曲线为O-P*，P*处的方位角为αP*；回旋曲线P1-P2的曲率变化率为kP12，初始回旋曲线为O-P2*，P2*处的方位角为αP2*；圆弧曲线P2-Q的圆心角为θ32，曲率为ρP2Q，初始圆弧曲线为O-P2′。

连接P7-P8，P8点为图1所示参考点的位置。

圆弧曲线P5-P6的半径取为Rmin。在调整路径中，为保证车辆能够跟随路径，允许的最大车度vmax2=0.75 km/h，P6-P7选择曲率变化率的最大值kmax2=2wmax。将P与P7点的横向距离LXPP7最小作为优化目标，调整路径规划转换为非线性规划：

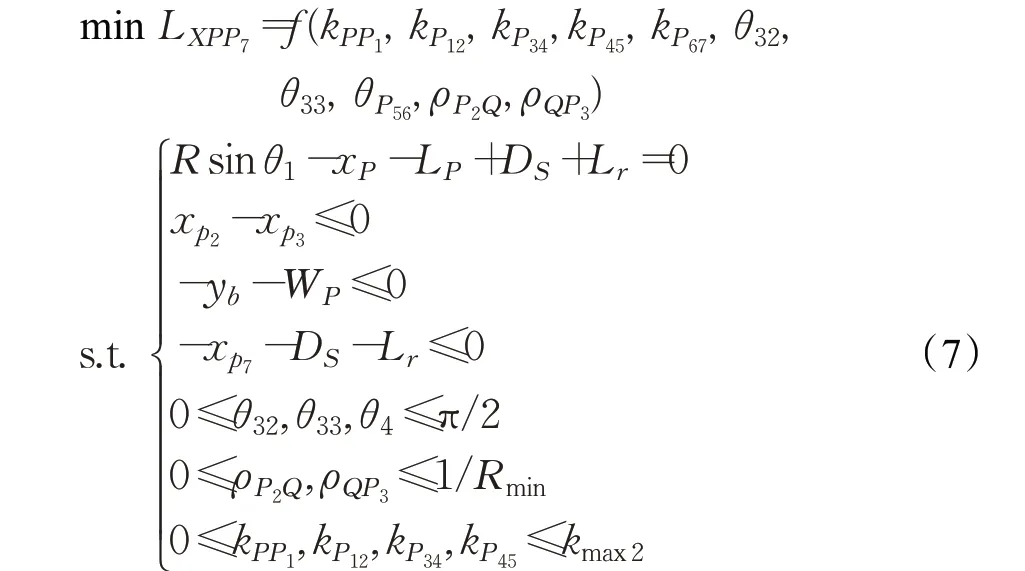
式中，第一个等式限定P点的位置关系；第二个不等式表示圆弧路径P2-P3存在性条件；第三个不等式表示车辆b点与障碍物BC侧不发生碰撞；第四个不等式表示车辆ab侧与障碍物AB侧不发生碰撞。

2 小车位下的泊车路径的跟踪控制

在泊车过程中车辆以低速行驶，根据阿克曼转向原理，车辆的运动学模型为：

式中，(x,y)代表参考点坐标，v代表车速，φ代表车辆航向角，δ代表车辆的前轮转向角。

传统路径跟踪的方法是将路径视作时间参考函数，若车辆跟踪过程中出现误差，这种误差会随着时间逐渐增加，甚至会直接导致车辆失去跟踪能力[25]。引入f=-x做为非时间参考量，车辆的运动学方程可表示为：

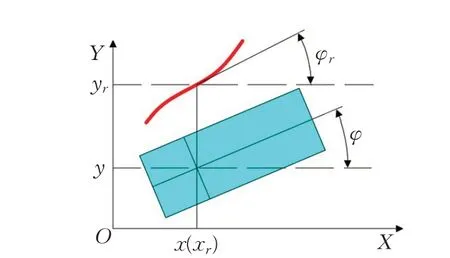
图5 路径跟踪偏差示意图Fig.5 Diagram of path tracking deviation

结合式（8）、（9）、（10），基于非时间参考变量的跟踪偏差为：

3 仿真分析

车辆的基本参数如表1所示。

表1 车辆基本参数Table 1 Basic vehicle parameters

泊车路径跟踪效果如图6所示。泊车过程中，汽车外轮廓与障碍物边界之间的相对位置如图7所示。

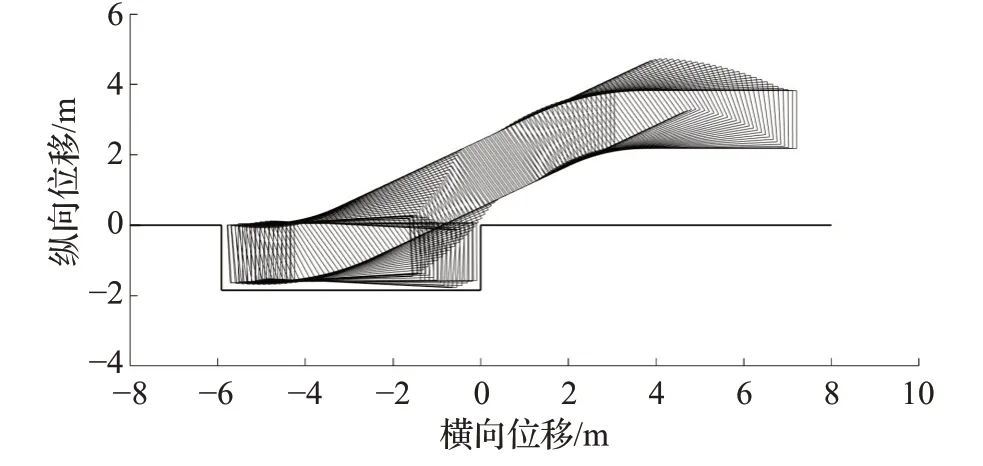
图7 汽车外轮廓包络图Fig.7 Envelope diagram of automobile outline

由图6、7 可知，车辆行驶路径与规划路径基本重合，汽车外轮廓的包络在行驶过程中未与周边障碍物产生碰撞，满足车辆避障约束及泊车要求等。

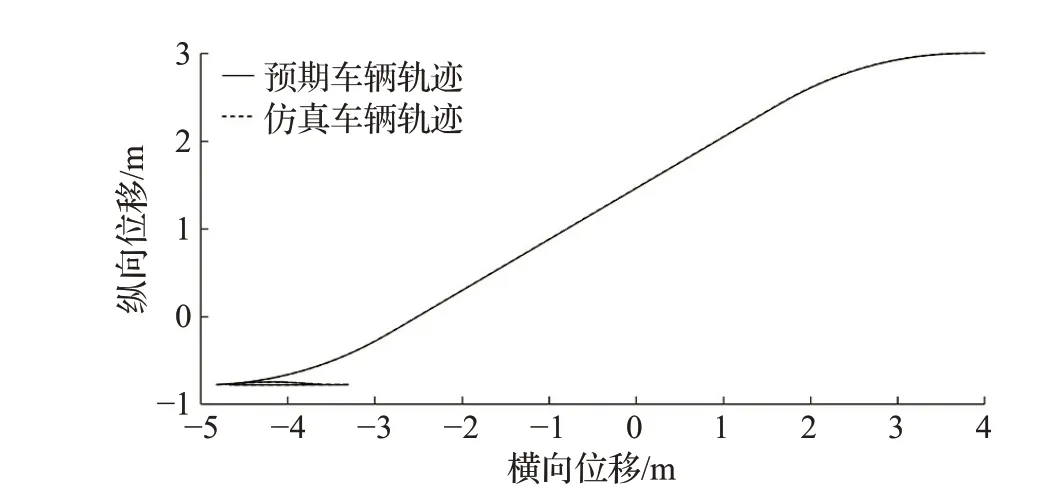
图6 路径跟踪效果图Fig.6 Diagram of path tracking

泊车过程中的纵向误差如图8所示。图8（a）、（b）、（c）分别表示泊入路径、前进调整路段和后退路段的纵向误差。

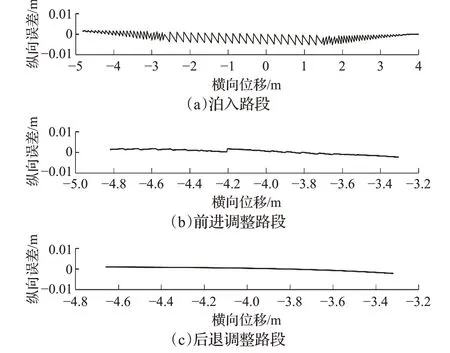
图8 路径跟踪过程中的纵向误差Fig.8 Longitudinal error in path tracking

由图8可知，泊入路段中的最大纵向误差为0.005 4 m；调整路径中的前进路段的最大纵向误差为0.002 2 m，后退路段最大纵向误差为0.002 1 m，泊车终止点的纵向误差为0.002 1 m。

泊车过程中的航向误差如图9所示。图9（a）、（b）、（c）分别代表泊入路段、前进调整路段和后退调整路段的航向误差。

由图9可知，泊入路径中的最大航向误差为0.114 6°；调整路径中的前进路段中的最大航向误差为0.401 1°，后退路段最大航向误差为0.383 9°，泊车终止点的航向角误差为0.383 9°。

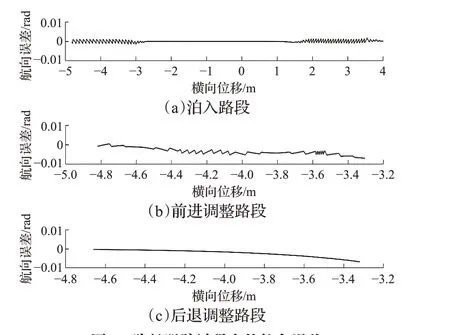
图9 路径跟踪过程中的航向误差Fig.9 Course angle error in path tracking

仿真过程中车辆的实际前轮转角如图10所示。图10（a）、（b）、（c）分别为泊入路段、前进调整路段、后退调整路段在不同函数作用下的前轮转角。

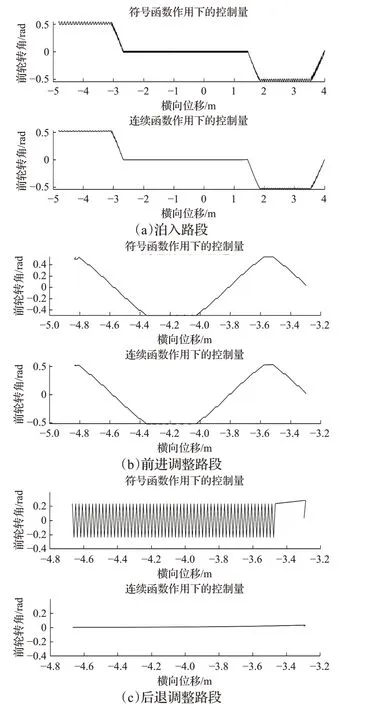
图10 不同函数作用下的前轮转角Fig.10 Front wheel rotation angle under different functions

由图10知，车辆在路径跟随过程中，前轮转角无突变，车辆行驶平滑；连续函数作用下的滑模控制器相比符号函数作用下的滑模控制器较大的抑制了高频抖振。

由图6～10可知，在滑模控制器的作用下，车辆与周围障碍物未发生碰撞，最大纵向误差为0.005 4 m，最大航向误差为0.401 1°，跟踪误差较小；全程前轮转角变化平滑，抖振抑制效果良好。

4 结论

对于小车位环境泊车难的问题，设计了泊入路径和调整路径，将回旋曲线、直线、圆弧曲线进行组合规划，实现了不同曲率路径之间的平滑过渡，该规划方法具有计算简便、曲率无突变的优点。基于非时间参考误差设计滑模控制器，将指数趋近率中的符号函数替换为连续函数，改善了泊车过程中的高频抖振问题。仿真结果表明，该路径规划方法满足小车位泊车的要求，前轮转角无突变、跟踪误差小，较好地解决了小车位泊车难、位姿调整难的问题。