Shrinking solitons上Ricci曲率的非负性*

张珠洪

(华南师范大学数学科学学院，广东 广州 510631)

一个黎曼流形(M,g)被称为gradient Ricci soliton(简写为GRS)，是指存在一个函数f和一个常数ρ，使得方程

Ric+▽2f=ρg

恒成立，其中Ric是流形的Ricci曲率张量，▽2f是势函数f的Hessian。注意到，如果势函数f是常数，那么GRS的方程将变成Ric=ρg。因此，GRS是Einstein流形的一个自然的推广。如果ρ>0，ρ=0或ρ<0，我们分别称之为shrinking，steady或expanding。Shrinking GRS对应于Hamilton的Ricci flow方程的自相似解，在Ricci flow的奇点分析中起到了非常重要的作用[1]。所以，理解和分类shrinking GRS是Ricci flow的一个核心课题。

一些类型的shrinking GRS已经被完全的分类，譬如3维情形[2]，局部共形平坦的高维情形[3-5]。近些年来，在这个课题上还有一些其他的进展[6-9]。事实上，许多关于soliton的研究工作都有一个显著的特征：soliton具有非负曲率。然而，不是所有的shrinking GRS都具有非负曲率[10-11]。尽管如此，在4 维的情形下，Munteanu-Wang[12]证明了4维有限数量曲率的非紧shrinking GRS上曲率算子是渐近非负的。

在本文中，我们主要研究shrinking GRS的曲率的非负性。在一个闭的shrinking GRS上，如果Weyl曲率满足一个拼挤条件，我们将证明Ricci曲率一定是非负的。

其中，{Wijkl}是Weyl曲率张量，而Ricci曲率张量Ric定义为Rik=gjlRijkl，数量曲率R=gikRik。

为了展示我们的主要结论，我们还需要引入一个关于对称矩阵的泛函，这个泛函可以刻画矩阵的特征值的一个分布特征。

定义1 设S是一个n阶对称矩阵，则

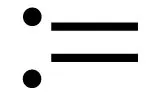
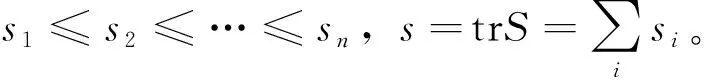
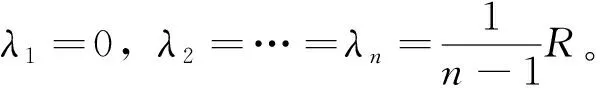
现在，我们可以展示本文的主要结论。

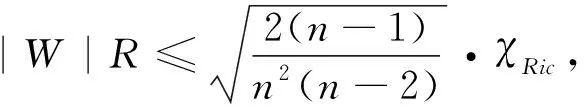
(i) Ricci曲率一定是非负的；

(ii) 如果进一步假设Ricci曲率是正的，那么它一定是平凡的，即是Einstein流形。

1 若干引理

设T是流形上的自共轭张量，h是光滑函数，那么，作用于T上的h-Laplacian是指

利用上述定义，我们可以陈述soliton上的一个基本方程[4]。

引理1 在一个 GRS 上，

为了更直观的揭示引理1中的元素Qij=RikjlRkl和|Rij|2，我们选择切空间上的一组基底{ei}，使得 Ricci 曲率张量对角化

(Rij)=diag(λ1,λ2,…,λn)

并且满足λ1≤λ2≤…≤λn。那么下述基本事实成立。

引理2

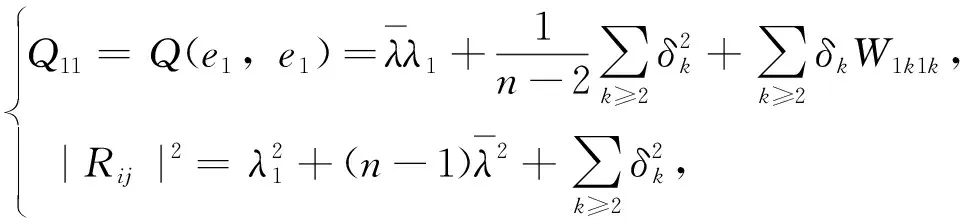
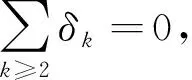
另一方面，利用黎曼如律张量的分解式，截面曲率

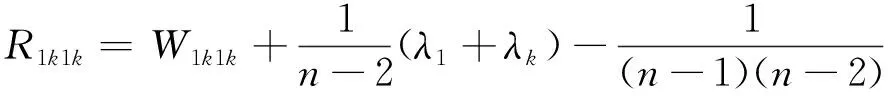
所以

证毕。

2 Ricci 曲率的非负性

现在我们可以来证明定理1了。

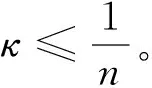
易由e1延拓得到Tp的一组单位正交基{ei}，使得每个ei都是Ricci曲率张量的特征向量，而且对应的特征值满足λ1=Ric(e1,e1)=κR≤λ2≤…≤λn。

另一方面，由极值原理，Δf(Ric-κRg)(e1,e1)≥0。从而根据引理1，

Q11-κ|Rij|2≤0

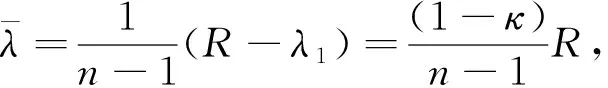
再利用引理2，可得

直接计算可知，

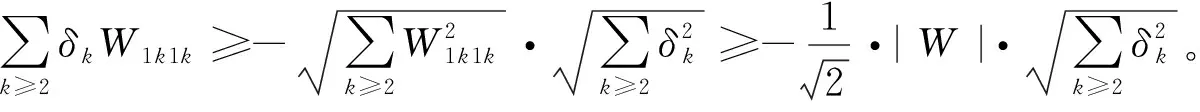
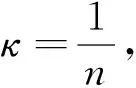
证毕。