三类Liénard系统极限环的下界*

熊峰 ，黄文韬

(1．上海财经大学信息管理与工程学院，上海 200433；2. 桂林航天工业学院理学部，广西 桂林 541004)

Liénard方程是微分方程中一类经典的方程。许多多项式系统可通过适当变换转变为Liénard方程的形式[1-2]。从而可利用Liénard系统的相关结果来分析，因此，对Liénard方程的研究具有重要的意义。

Liénard方程一般式为

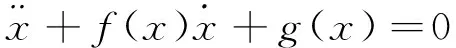
(1)

与其等价的一阶微分方程组形式如下

(2)

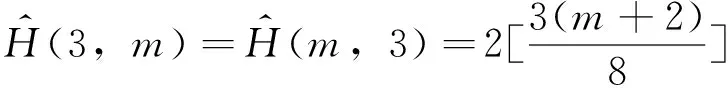
表1 Liénard方程的值[8]Table 1 Values of the Liénard equation [8]

☆：本文研究的内容；→：取值的递增趋势。

1 基本定义及引理

考虑一类实多项式系统

(3)

其中Xk(x,y),Yk(x,y)是关于x、y的k次齐次多项式。系统(3)通过如下复变换，

z=x+yi,w=x-yi,

(4)

可得其伴随复系统

(5)

其中z,w,T,aαβ,bαβ都是复变量且系数aαβ与bαβ满足共轭关系，即

引理1[9]对于系统(5)， 我们能够逐项确定形式级数

(6)

使得

(7)

其中，c00=1，当α<0，或β<0，或α=β>0时，cαβ=0，其他情况的cαβ由递推公式

(8)

给出。对任意正整数m，μm由递推公式

(9)

给出，其中μm称为系统(5)的第m个奇点量。

定义1[10]对系统(5)而言，如果μ1=μ2=…=μk-1=0,μk≠0，则称原点为系统的k阶细奇点。

由文[10]知，系统(3)的首个非零焦点量ν2m+1(2π)与其伴随复系统的首个非零奇点量μm满足

ν2m+1(2π)=iπμm

(10)

因此，系统(3)焦点量的计算可以化为系统(5)奇点量的计算。

2 一类Liénard方程(m=9,n=7)的极限环

2.1 伴随复系统的奇点量

考虑如下一类Liénard方程：

(11)

其中a3,a4,a5,a6,a7,a8,b3,b5,b6∈R。通过变换(4)，系统(11)转化为其伴随复系统：

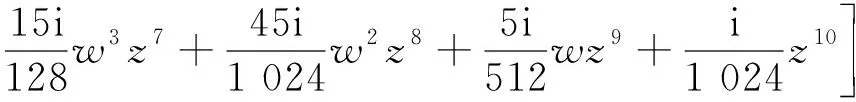
(12)

由引理1的递推公式，用Mathematica软件进行计算，得到系统(12)原点的前10阶奇点量。

定理1 系统(12)原点的前10阶奇点量如下：

其中计算μk时已置μ1=μ2=…=μk-1=0,k=2,3,…,9。

2.2 中心存在性与极限环分支

根据前一节的计算和分析，我们接着讨论系统的中心问题与极限环分支问题。由定理1有

定理2 对于系统(11)或者(12)，原点既不是系统(11)也不是系统(12)的中心。

证明若原点是系统(12)的中心，则有μ1=μ2=μ3=μ4=μ5=μ6=μ7=μ8=μ9=μ10=0成立。由μ1=μ2=μ3=μ4=μ5=μ6=0，有

又μ7=μ8=μ9=μ10=0，即求解方程组F2=F3=F4=F5=F6=0是否存在公共解。因为Fj(j=2,…,6)仅含有4个独立变量，a4、b3、b5和b6，所以我们首先求解方程组F2=F3=F4=F5=0的实数解，然后将满足方程组的实数解代入F6，并验证其是否为零，若为零，则系统(11)或(12)的原点为中心，反之，定理得证。经仔细计算，方程组Fj(j=2,3,4,5,6)存在3组实数解，将这3组实近似解(精确到小数点20位)代入F6表达式中，均得出F6≠0，即μj=0(j=1,2,…,9),μ10≠0。这个结论也可用Gröbner来说明，由计算机代数软件Mathematica计算理想[μ1,μ2,μ3,μ4,μ5,μ6,μ7,μ8,μ9]的Gröbner基，得到

GroebnerBasis[{μ1,μ2,μ3,μ4,μ5,μ6,μ7,μ8,μ9,μ10},

{a3,a4,a5,a6,a7,a8,b3,b5,b6}]={1}

这就说明方程组μ1=0,μ2=0,…,μ10=0没有公共实根。

因此，原点既不是系统(12)的中心，相应地，也不是系统(11)的中心。

由定理2的证明，我们有

定理3 对于系统(11)，原点为细焦点的最高阶数是10，并且原点为系统(11)的10阶细焦点(系统(12)的10阶细奇点)当且仅当

Fj=0 (j=1,…,5)

(13)

为了便于应用，从定理2的证明中取满足条件(13)的一组实数解

a4= 19.357 334 947 696 801 244,

b3= 2.197 337 880 236 531 145 5,

b5=-0.851 084 727 246 997 987 2,

b6= 3.770 104 155 316 207 683 2

(14)

在证明系统(11)极限环存在性之前，由文 [12]的定理2有

引理2[12]对系统(3)，其伴随复系统在原点处的奇点量μi(i=1,2,…)有k个线性无关的参数θ=(θ1,θ2…,θk)，当θ=θk时，原点为系统(5)的k阶细奇点(相应地系统(3)的k阶细焦点)，且雅克比行列式满足

(15)

则系统(3)在原点的充分小邻域内可扰动出k个小振幅极限环。

下面我们给出这节的主要结论

定理4 对于系统(11)来说，当系数满足式(13)时，通过适当的微扰，系统在原点充分小的邻域内可分支出10小振幅极限环。

证明由定理3知，当条件(13)成立时，原点是系统(12)的10阶细奇点(系统(11)的10阶细焦点)。通过计算如下的雅克比行列式可得

≈0.314 411 474 338 970 058 837 456

114 802 019 923 751 699 037i

≠0

由引理2 知系统(11)在原点的充分小邻域可分支出10个极限环。

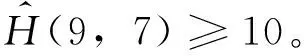
3 一类Liénard方程(m=8,n=7)

的极限环

考虑如下一类Liénard方程：

(16)

其中a3,a4,a5,a6,a7,b3,b5,b6∈R。与上一节的讨论类似，由引理1的递推公式，我们计算得到系统(16)的伴随复系统原点的前9阶奇点量

其中

F1=35-42a6+28a4b3-20a4b6,

F2=-392+245b3+196a4b5-

F3= 196a4+ 175b5-200b6,

F4= 49 049 + 8 330b3b5-

F5= -3 878 448 + 1 027 530b3-

415 669 009b5+ 79 539 600b6+

定理5 对于系统(16)或者它伴随复系统来说，原点不是系统的中心，系统(16)原点为细焦点的最高阶数是9。

证明与定理2的证明类似，经求解方程组μ1=μ2=μ3=μ4=μ5=μ6=μ7=μ8=0，可以得到该方程组的两组实数解，把每一组实根代入μ9表达式中均得到μ9≠0,即μ1=μ2=μ3=μ4=μ5=μ6=μ7=μ8=μ9=0不成立，故原点不是系统(16)的中心。由于方程组μ1=μ2=μ3=μ4=μ5=μ6=μ7=μ8=0

存在实数解且这些实数解不满足μ9=0，这说明系统(16)原点为细焦点的最高阶数是9。

为了方便应用，我们列出满足方程组μ1=μ2=μ3=μ4=μ5=μ6=μ7=μ8=0的其中一组解

a3=0,

a4=2.505 136 670 577 324 215 529

487 258 943 623 802 995 196 181 84,

a6=4.338 235 294 117 647 058 823 529 411 764

705 882 352 941 176 471,

a5=0,

a7=2.004 109 336 461 859 372 423 589

807 154 899 042 396 156 945 472,

b3=-3.029 329 095 027 754 987 049 753 689 561

914 281 085 085 280 421,

b5=-11.010 486 326 684 476 051 279 386 309

478 163 334 304 471 362 4,

b6=-7.179 141 598 683 138 813 650 565 507 028

641 590 581 120 183 896

(17)

与上节讨论类似，经计算得到

≈0.019 980 299 989 610 697 391 439

548 663 761 472 146 146 285 25i

≠0

那么，我们可以得到

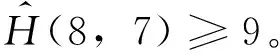
4 一类Liénard方程(m=7,n=8)

的极限环

考虑如下一类Liénard方程：

(18)

其中a2,a3,a4,a5,a6,b3,b5,b6∈R。

由引理1的递推公式，并通过计算，我们可以得到系统(19)伴随复系统原点的前9阶奇点量。

定理7 对于系统(18)的伴随复系统原点前9阶奇点量如下：

μ4=

i(490a2+ 2646a6-2205b3-882a2b5+

其中

F1= -33 271 + 6 174a2-3 430a2b3+

15 435b5+ 4 900a2b6-11 025b3b6-

F2= 27 783 + 2 450a2-11 025b3-

4 410a2b5-14 805b6-2 268a2b6+

F3= -39 991-5 950a2+ 3 570a2b5+

18 360b6+ 1 836a2b6

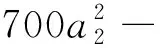
4 185 138 132b6+ 211 951 971 000a2b6+

F5= 27 312 518 314 948 419 +

4 364 166 372 961 248a2+

23 890 340 539 800b3-

1 456 897 687 875 000a2b3-

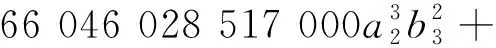
34 890 558 192 000b5-

1 254 074 736 163 2840b6-

1 158 914 850 102 594a2b6-

10 238 717 374 200b5b6+

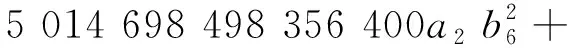
定理8 对于系统(18)，原点不是系统中心。

证明利用计算机代数软件Mathematica可计算理想[μ1,μ2,μ3,μ4,μ5,μ6,μ7,μ8]的Gröbner基，经计算有

GroebnerBasis[{μ1,μ2,μ3,μ4,μ5,μ6,μ7,μ8,μ9}

{a2,a3,a4,a5,a6,b3,b5,b6}]={1}

从而得到方程组μ1=0,μ2=0,…,μ9=0没有公共实根，即μ1,μ2,μ3,…，μ9不可能同时为0。

因此原点不是系统(18)的中心，相应地，也不是其伴随复系统的中心。

由定理8及其证明过程，有

定理9 系统(18)原点成为细焦点(其伴随复系统原点的最高阶细奇点)的最高阶数是9，且系统(18)原点是9阶细焦点(其伴随复系统原点是9阶细奇点)当且仅当下列条件成立

490a2+ 2646a6-2 205b3-882a2b5+

Fj= 0,(j= 1,2,3,4)

(19)

同样，我们取满足条件(19)的一组实近似解

a2=-81.432 996 679 011 493 893

475 288 856 750 791 764 998 304 380 62,

a3=0,

a4=-86.385 261 993 928 019 814 143

108 603 282 946 233 527 880 282 13,

a5=-32.573 198 671 604 597 557

390 115 542 700 316 705 999 321 752 248,

a6=9.944 522 844 463 895 178 373

749 713 016 379 278 370 120 643 467,

b3=2.609 896 880 706 486 009

523 895 483 236 786 943 931 106 542 814 7,

b5=1.240 113 171 962 005 605

683 194 812 100 897 603 723 212 727 111 4,

b6=0.640 596 345 108 271 448 288

583 043 911 072 911 480 884 214 849 7

(20)

为证明极限环的存在性，需计算如下行列式

若J≠0，则系统(18)在适当的扰动下在原点邻域能够产生9个极限环。

经计算

J≈1.217 128 561 716 344 016

685 096 492 253 207 367 460 16i≠0

那么，由引理2有