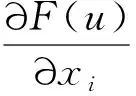一类含hysteresis的自控系统模型*
徐伟,孙涛
(1.南京航空航天大学经济与管理学院,江苏 南京 210016;2.南京审计大学会计学院,江苏 南京211815)
很多自动控制系统都具有某种时滞(hysteresis)效应,例如自动恒温系统中温度由上升突然转为下降(或由下降突然转为上升),自动控制的空调器通常都不能立刻同步做出反应,往往要滞后一段时间才从降温状态转向增温状态(或反之)。由于时滞因素的非线性特点,函数的很多优良性质遭到破坏,含有时滞的模型分析起来十分困难,所以在含时滞的自控系统建模中,人们通常都略去时滞因素[1-2]。这样往往使得构造出来模型对反映系统的真实状况过于粗略,设计出来的控制方案误差较大。目前人们对时滞现象的特点认识还很肤浅,对于具时滞的微分方程,仅对某些特殊的方程在特殊条件下有弱解存在性结果,而解的唯一性稳定性基本上还没有结果。近年来随着治理空气污染日益受到人们的关注,各种空气净化器应运而生,净化设备的净化过程都具一定程度的时滞效应。空气净化器又称空气清洁器,是指能够吸附、分解或转化各种空气污染物(一般包括PM2.5、粉尘、花粉、异味、甲醛之类的装修污染、细菌、过敏原等),有效提高空气清洁度的产品。空气净化器中有多种不同的技术和介质,使它能够在不同条件下向用户提供清洁和安全的空气。常用的空气净化技术有:吸附技术、负(正)离子技术、催化技术、光触媒技术、超结构光矿化技术、HEPA高效过滤技术、静电集尘技术等;材料技术主要有:光触媒、活性炭、合成纤维、HEAP高效材料、负离子发生器等。现有的空气净化器多采用复合型,即同时采用了多种净化技术和材料介质。空气净化器主要分为家用 、商用、工业、楼宇。在雾霾易发的城市,空气净化器有望像电视、冰箱一样在家庭中普及。生产过程中有大量粉尘或有毒气体产生的建筑工地、工厂车间,如人造板生产车间,纺织厂车间,印刷车间等,空气净化器将成为重要的治污和改善工人工作环境的设备之一。特别是生产过程中有大量有害气体需要净化处理的大型企业,净化设备的投入是一笔很大的费用,随着全球经济不景气和治理污染压力的不断加大,精打细算地减少生产成本是企业必须面对的一项长期任务。精确测算净化效果是企业核算净化成本、编制和选择净化投资方案必不可少的重要环节。由于净化设备的hysteresis效应,使得精确的测算净化的动态效果十分困难。所以长期以来,人们主要凭经验选择空气净化设备,结果要么净化效果达不到理想,要么投资过大。但在计算工具十分先进的今天,探讨hysteresis效应的规律,利用计算机模拟净化器的工作过程,跟踪测算出净化的动态效果已经成为可能,根据净化治污需要达到的目标,合理选择功能匹配的净化器和安排使用时间无疑是十分有意义的问题。
静态地测定空气净化器平均净化效果,不少学者讨论过。如赵亢等[3]对6种空气净化器,提出了3种测试净化效果的模式。2008年张琴等[4],2015年宋静等[5]分别关于空气净化器对甲醛、苯和氨气的净化效果的测试方法进行了研究。张言等[6]对空气净化器在室内环境中的空气净化效果进行了测试研究。厉龙等[7]提出空气净化器对净化甲醛效果的测试方法。何锦强[8]对空气净化器净化室内TVCO效率做出了实验研究。2006年我国还发布了第一部《室内空气净化产品净化效果测定方法》(QB/T2761-2006),并于2006年12月1日正式实施。作为各种室内空气净化产品净化效果测定的统一规范,为消费者选择净化器提供指导。2015年我国又发布了GB/T 18801—2015 空气净化器国家标[9]。国外学者也有类似研究[10-14],但是到目前为止,国内外学者们提出的净化效果测试方法和我国政府发布的净化效果测试方法,都是指在室内没有新的污染源产生条件下,空气净化器运行一段时间后,相对于净化前空气中污染物平均降低的程度,不能用于有新污染物不断产生的生产工地和车间动态地跟踪测试每个点污染物浓度。
本文以吸附式空气净化器实施工业减排为例,讨论具有hysteresis的自控系统成本与效益的计算问题。首先根据空气净化系统的功能原理引进了一类时滞算子F及其伴随算子G,通过一系列的分析,推算给出了算子F和算子G的若干重要性质,特别的得到了函数在算子F作用下保持关于时间变量的可导性。然后主要利用不动点定理证明了两类含时滞项的微分方程整体古典解存在唯一性。使得动态地跟踪分析空气净化过程中,净化区域内每点污染物浓度成为可能。最后考虑了企业粉尘或VOCs(Volatile organic compounds挥发性有机物,根据美国国家环保署的定义,不包括CO,CO2,碳酸、碳酸盐、金属碳化物及碳酸钙)等有害物净化问题,拟在政府实施有害气体排放管制背景下,通过对空气净化器功能的定量分析,根据净化需要达到的目标,建立净化器投资决策模型,为企业合理选用净化设备提供参考。本文的不足在于未能得出函数在算子F作用下是否能保持对空间变量的可导性,因此对于时滞项关于空间变量可导的微分方程还有待进一步研究。
1 自控系统与hysteresis现象
以吸附式净化器为例,并假设只吸附空气中一种污染物。设在空间区域Ω内点(x,y,z)处,时刻t空气中污染物的质量浓度为u(x,y,z,t)(单位:mg/m3),空气净化器对污染物的吸附强度为v(x,y,z,t)=F(u(x,y,z,t))=F(u)(单位:mg ·m-3·s-1),当然吸附强度与净化器吸附能力、空气中污染物的质量浓度u(x,y,z,t)以及点(x,y,z)到净化器吸口的距离有关。再设空气中污染物最大质量浓度为u*,最小质量浓度不妨记为0(指低于这个质量浓度,空气净化器就会自动停止吸附),净化器的最大吸附强度为v*,最小吸收强度为0,考虑的时间段为[0,T]。取函数集合
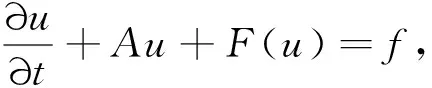

图1 算子F映射规律示意图Fig.1 Mapping law of operatorF

Hysteresis算子不只是不满足线性那么简单,主要麻烦在于F(u(t))的值不仅依赖u(t)的值,还依赖于u在时刻t前后的变化趋势,从而含hysteresis的微分方程讨论起来十分困难。所以对Hysteresis算子形态的讨论还十分罕见,对含Hysteresis的微分方程古典解差不多还没有结果。
2 算子F的严格定义和性质

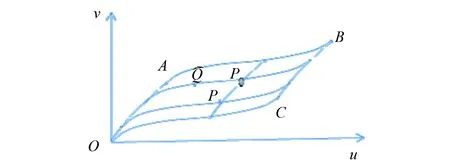
图2 算子F0映射标准化图Fig.2 Mapping Normalized Graph of operatorF0
0<γ≤|g′(u)|,|h′(u)|≤δ,即过Σ上任意点沿轨线或基线的导数都介于γ和δ之间。净化器灵敏度越高,点A与点B越向直线段AB靠拢,即时滞池Σ变得越狭窄,若净化器灵敏度极高,整个时滞池Σ几乎变成一条直线段。一般δ≤1,从而v*≤u*,N⊆M。
2.1 算子F0的定义和性质
由于算子F具有时滞效应,对一般连续函数直接定义F0不方便,我们首先只对分段函数定义F0。对任意u(t)∈M分段单调,定义初值
v(0)=F0(u(0))=
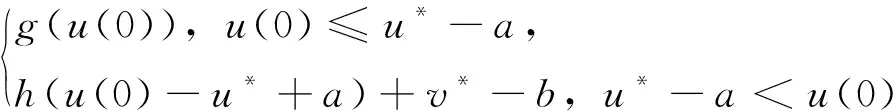


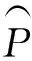
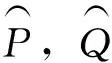
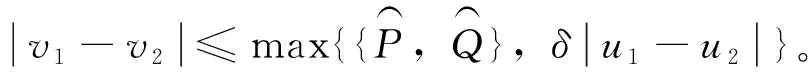
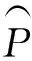
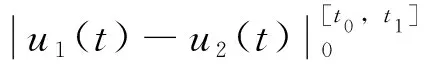
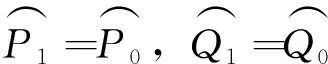
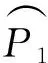
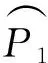
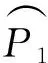
由F0初值定义,对任意u1(t),u2(t)∈M,显然|v1(0)-v2(0)|≤δ|u1(0)-u2(0)|,根据引理1和引理2,若u1(t),u2(t)都分段单调,对于任意t0∈[0,T],利用数学归纳法容易推得
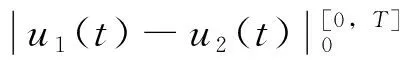
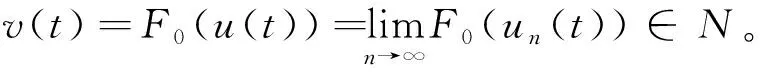
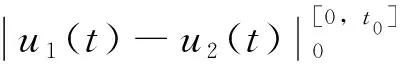
对任意t0∈[0,T]
(1)
推论1 对任意u(t)∈M,均有
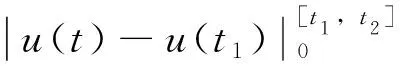
对任意[t1,t2]⊂[0,T]
(2)
事实上,令u1(t)=u(t),当0≤t≤t1时,u2(t)=u(t),当t1 |v1(t2)-v2(t2)|=|v(t2)-v(t1)|, |u1(t)-u2(t)|=|u(t)-u(t1)| 推论2 对任意u(t)∈M,关于t绝对连续,则F(u)关于t也绝对连续。 (ii)设|(x1,y1,z1)-(x2,y2,z2)|<1,则 由推论1, 于是,得到 定理1结论成立。 G(u(x1,y1,z1,t1))= G(u(x2,y2,z2,t1))= 通过一些基本计算可得 |G(u(x1,y1,z1,t1))-G(u(x2,y2,z2,t1))|≤ 2|g′(u(x1,y1,z1,t1)-u1*)- g′(u(x2,y2,z2,t1)-u1*)|+ 注意到 |g′(u(x1,y1,z1,t1)-u1*)- g′(u(x2,y2,z2,t1)-u1*)|≤ 因此,若|(x1,y1,z1)-(x1,y1,z1)|≥1,则 若|(x1,y1,z1)-(x1,y1,z1)|<1,则 δ(|x1-x2|+|y1-y2|+|z1-z2|)/ |G(u(x2,y2,z2,t1)-G(x2,y2,z2,t2)|= 设某车间(或工地 )生产过程中每天有气态污染物产生,为了防止污染扩散,车间(或工地)对外封闭,内部配置功率强大的净化器。产生的气态污染物密度函数为f(x,y,z,t), 0≤f≤u*,车间内空气中污染物质量浓度为u(x,y,z,t),净化器吸收的强度一般为F(u(x,y,z,t))相当于负源。u满足如下反应扩散方程系统 (3) (4) (5) (6) 其中β>0为常数,依赖于污染物的类型、净化器的品质、有关物理量的计量单位等因素,ν为单位法向量。 下面仅对系统(4)-(6)解的存在唯一性给出证明,其方法可稍作调整用于证明系统(3)-(5)解的存在唯一性。由定理2,式(6)可变形为 (7) 再设方程(4)-(6)有两个解u1,u2∈M∩E,则 [F(u1)-F(u2)]=0 in Ω×(0,T] (8) (9) (10) e-λt[F(u1)-F(u2)]in Ω×(0,T], (11) 由Hopf引理(参见文献[19 ]),U的正最大值,和负最小值都不可能在∂Ω×[0,T]上达到。下面用反证法证明U≡0。设U的正最大值在点(x0,y0,z0,t0)∈Ω×(0,T]处达到,显然(x0,y0,z0,t0)也是u1-u2在Ω×(0,t0]内的正最大值点。否则存在点(x1,y1,z1,t1)∈Ω×(0,t0]使 u1(x1,y1,z1,t1)-u2(x1,y1,z1,t1)> u1(x0,y0,z0,t0)-u2(x0,y0,z0,t0)>0 (12) 但e-λt1≥e-λt0且 U(x0,y0,z0,t0)= e-λt0[u1(x0,y0,z0,t0)-u2(x0,y0,z0,t0)]≥ e-λt1[u1(x1,y1,z1,t1)-u2(x1,y1,z1,t1)]= U(x1,y1,z1,t1) (13) 式(12)与式(13)不相容。 由式(11),得 (1-εδ)λ[u1(x0,y0,z0,t0)-u2(x0,y0,z0,t0)]≤ λ[1-εG(u1)]· [u1(x0,y0,z0,t0)-u2(x0,y0,z0,t0)]≤ -δ[u1(x0,y0,z0,t0)-u2(x0,y0,z0,t0)]+ 从而 (14) 仍然以空气净化为例,考虑企业生产过程中有某类VOCs气体产生。这类VOCs气体直接对外排放会污染环境,而且最终产品中往往还会含有少量不易除尽的气态有毒物质,在今后的产品使用过程中,这些气态有害物质将缓慢释放,对人造成伤害。政府通常规定最终产品中这种气态有毒物质含量的某种标准(如甲醛的E1标准,质量浓度小于等于1.5 mg/L),保证产品不对用户造成伤害。 假设1 政府对企业的生产实施双约束,每年VOCs气体总排放配额为H0(t),产品中有毒气态物质质量浓度限额为ω0(mg/L)。“工艺减排”技术已经用到最大限度,现在拟对VOCs气体采用净化处理,产品单位生产成本为c0,正常售价为p0,年产量为Q0,固定生产成本为C0。总排放配额允许市场交易,交易价格为σ,产品中有毒气态物质限额无法交易,但含量每低于ω一个单位,销售价格可提高ρ能被消费者接受。 企业根据生产的工艺技术流程、生产设备的先进程度、每批计划产量、产品预计达到的质量等因素,用电脑模拟出每个生产加工周期[0,T1]中产生VOCs源的密度函数f(x,y,z,t),测算出可能释放到Ω内VOCs总量的理论值I0。 注1 为了便于对有害气体的处理,通常都会把Ω限制在一个狭小的空间内,如人造板材去毒气过程通常是把板材密封在罩子里加热,在罩子周围使用功能强大的净化设备吸收毒气。生产实际中Ω往往都是低矮扁平的,还可以把Ω近似地看成平面区域。 假设2 总结同类企业经验、根据企业生产规模和边际效应递减规律,投资与净化效果大致满足下列微分方程 (15) (16) 其中H表示每个生产批次净化减排量,ω表示减少最终产品中含毒物质量浓度,s为净化设备投资,0 σ[m(I0-c1sr1)-H0]-s-C0 (17) s1-r2+mc1r1sr1-r2σ-c2r2ρQ0=0 (18) σ[m(I0-c1sr1)-H0]-s- (19) (20) (21) 由(21)-(23)算出唯一精确古典解w,再把u=e-0.9tw代入(3)-(5)检验,若误差不大,就用方程(19)-(21)取代方程(3)-(5)作决策,计算难度减少很多。 同样方程(6)转化为 (22) 由(22)-(24)也能算出唯一精确古典解w。2.2 算子F的定义和性质
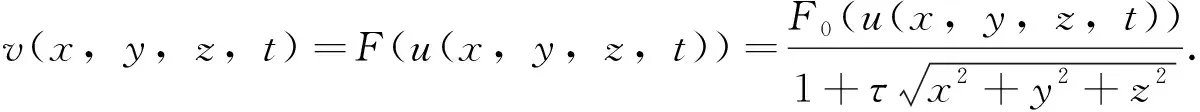
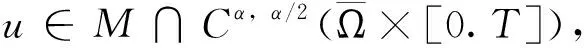
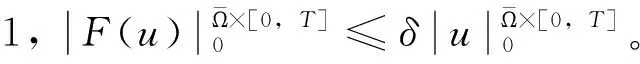
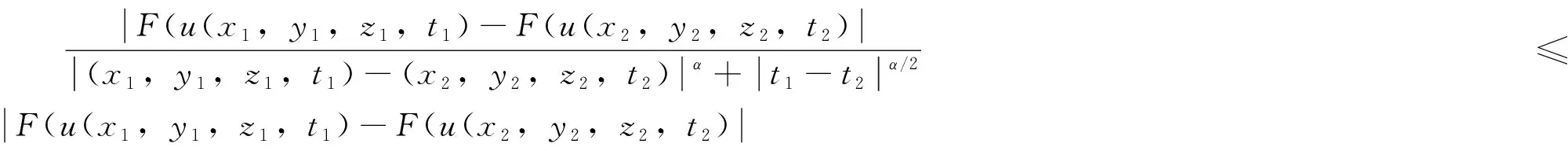
3 算子F的伴随算子G及其性质
4 含hysteresis的微分方程

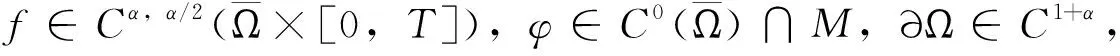
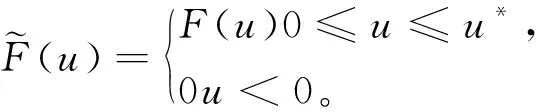

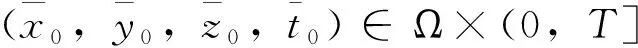
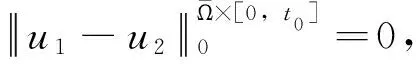
5 含hysteresis的系统运行成本与效益评价模型
5.1 有害物总排放量和最终产品中有毒物含量双约束模型
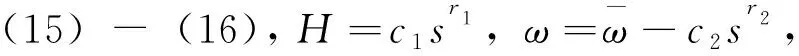
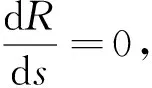
5.2 工作场所有害物含量约束模型
6 结 语