数形结合思想在高中物理解题中的应用

郭媛霞

摘要：在高中物理解题中巧妙运用数形结合思想，能够使抽象的问题直观化、复杂的问题简单化，有利于提高物理解题效率与能力，因此教师要加强对数形结合思想方法的内涵、特点与要求的教学，让学生掌握数形结合思想在物理解题中的运用方法，加强解题应用训练，才能提高数形结合思想在高中物理解题中的应用成效，从而促进学生物理解题能力的提升.

关键词：数形结合思想;高中物理;解题应用

中图分类号：G632文献标识码：A文章编号：1008-0333（2022）18-0106-03

数形结合是重要的数学思想，通过借助于“以形助数”和“以数解形”的优势和作用，就能实现抽象问题直观化、复杂问题简单化，从而使学生容易理解掌握所学知识和提高解决问题的能力与效率.把数形结合思想用于高中物理解题中，通过把物理过程图形或物理量之间的函数关系图像与物理量之间进行相互转化，有利于学生提高解题能力，因此教师要加强数形结合思想方法在高中物理解题教学中的应用，以此来促进学生物理解题能力的提升.

1 数形结合思想的内涵

数和形是数学研究的基本对象，“数”表示各种运算，其基本特点就是可以进行运算并且能够精确表示;而“形”表示各种图形、图像，其基本特点是直观、形象.数与形不是独立存在的，它们之间具有联系、可以相互转化.

2 数形结合思想在物理解题中的应用要求

数形结合思想虽然是数学思想，但用于高中物理解题同样适用，而且具有特殊优势并能发挥独特作用，但在高中物理解题运用时要注意如下要求：

一是坚持等价原则.由于数形结合思想的本质就是数与形的等价转化，因此在高中物理解题中，数（物理量及其之间的函数关系式）与形（物理图形或图像）的转化要遵循等价原则，这样才能保障数形结合思想运用的准确性和有效性.

二是坚持双向原则.数形结合思想在物理解题运用时，做到既对物理图形或图像进行分析，同时也要对物理量及其函数关系式进行分析，而不能片面地只对数或形进行分析，这样才能全面发挥数形结合思想的优势和作用.

三是坚持简单原则.数形结合思想的特点和应用目的，就是要把抽象、复杂的物理问题变成直观形象、简单的问题进行处理，因此在应用数形结合思想进行物理解题时，要通过该思想方法的运用，能使物理问题变得简单化，否则就难以达到数形结合思想应用的目的.

3 数形结合思想在物理解题中的应用方法

3.1 以形助数简化抽象物理问题

对于一些抽象、复杂的物理问题，在解题中可能会难以把握各物理量之间的关系，难以找到解题的思路或突破口.如果对物理图形或运动过程的图像、受力分析图等进行详细观察与分析，就能把形象直观的图形语言转化成某些物理量具体数据，以此来发现更多的解题条件，或者利用图像建立物理量之间的函数关系式，就可以找到解题的思路或突破口，使抽象复杂的问题变得简单直观，从而能够提高物理解题效率.

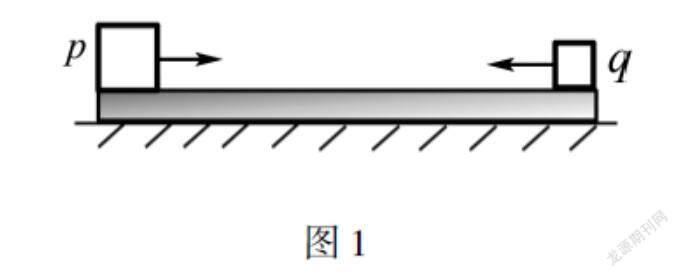
例1在图1中，两个物体的质量分别是mp=1 kg，mq=5 kg，两物体放在与水平地面静止的长木板的两端，它们与木板的动摩擦因素是μ1=0.5;长木板与地面的动摩擦因素是μ2=0.1.在某一时刻这两个物体开始相向移动，初速都是v0=3 m/s.当两个物体相遇时，q物体正好和木板相对静止.（假如最大静摩擦力等于滑动摩擦力，g=10 m/s2）.

求解如下问题：（1）p与木板相对静止时，木板的速度是多少？（2）两物体开始移动时，它们之间的距离是多少？

解析本题作为一道综合性比较强的题目，具有较强的抽象性和复杂性，虽然本题目可运用多种方法解题，但都相对比较复杂.如果运用数形结合方法，画出物体运动的v-t图就能很容易地求解此题.可根据题意并根据动力学的知识做出图2所示的v-t图.

（1）从图上可直观地看出0.4秒后p物体与木板相对静止，

即t1=0.4 s，木板的速度是v1=1 m/s.

（2）根据图像的物理意义可求出q物体和地面的位移是sq=S△OEC-S△DEF=0.875m;在t1（0.4s）时间内p物体相对地面的位移是sp=S梯形ABGO=0.8m，在t2（0.3s）时间内，p物体相对地面的位移是梯形BDFG的面积，s1=S梯形BDFG=0.225m，这样就可求出p、q两物体在开始运动时的距离是s=sq+s1+sp=1.9m.在本题求解中，通过借助于v-t图形，就能直观地表示两物体的物理量及其数量关系，在求解本题时还要对物体受力、运动情况进行准确分析，才能准确解题.

3.2 以数解形发现规律解决问题

在高中物理解题中，借助于图形、图像进行解题是有效的方法，也是每个学生喜欢运用的方法，从图形上能表示或看出与物理问题相关的数据或信息，但是图形、图像在提供直观信息的存在着准确性不高的问题，要想精确地求解物理问题，需要通过精确的数量计算才能发现其规律，找到解决问题的方法或答案，因此在物理解题中，需要把图形与物理量的计算有机结合，通過精确计算来精确表示物理图形或图像的物理含义，从而能实现准确解题.

3.3 数形结合提升解题思维能力

利用数形结合思想不但能提高物理解题效率，还能提升学生的物理解题思维能力，包括转化思维、逆向思维、创新思维、等效思维、综合类比等多方面的思维能力，这样就能从根本上提升学生物理解题能力，因此教师不但要注重利用数形结合思想引导学生解决物理问题，还要注重在解题中利用数形结合来提升学生物理解题思维能力.

例2求图3（1）所示电路A、B两端的总电阻是多少？

解析本图中的各电阻之间的串关联关系比较复杂，不能直接运用串关联公式求解，如果转换思维对该电路进行等效转化，就容易解决该问题.可从A→B给每个节点标上a、b、c，然后把每个电阻根据节点编号进行等效连接，就可得出等效电路，就容易求出总电阻.通过借助“形”的转换，能培养学生等效思维，而且等效思维在物理解题中经常应用，对促进学生物理解题能力提升有重要益处.

在解决高中物理问题中，经常会遇到一个物理问题中包含多方面的影响因素，要有效解决这类物理问题，需要具备全面抽象与概括、分析与综合以及抓主要矛盾的思维能力，这样才能找到物理问题的主要特征或影响因素，忽略次要因素，就能简化问题有利于解决问题.运用数形结合思想，可以帮助学生建立物理问题的模型，有利于学生掌握物理问题的本质特点或规律，能培养学生的抽象与概括、分析与综合思维能力.如，在图3（2）中通过运用电路符号，就能将复杂抽象的电路通过抽象与概括、分析与综合，将能容易解决图3（1）中的物理问题;再如，计算匀强电场类的物理问题时，就可以按照极板间的距离与其长度相比非常小、且忽略边缘效应等次要因素下进行解题，就能简化问题，有利于解决问题.

3.4 数形结合创新物理解题方法

数形结合思想对创新高中物理解题方法具有重要的作用，既能简化问题提高物理解题效率，又能增强准确性提高解题质量.在物理解题中，教师应重视指导学生加强对物理图形、图像特点与性质的研究，充分利用函数图像中的斜率、图形围成的面积、直线的截距、图形中线段或曲线的交点等重要参数来创新物理问题的解决方法.此外，利用数形结合思想还能创新解决物理实验类的题目，简化实验类题目的解题方法，提高物理实验类题目的解题效率.

例3要求出某电压表的内阻，某同学运用如下实验器材：电压表V（内阻RV）、可变电阻器R、开关、二节干电池E（内阻忽略），并将这些器材串联起来形成实验电路.然后改变可变电阻R的数值，观察电压表的数值，得出如下实验数据表格.

R/Ω200.0400.0600.0800.01000.01060.0U/V2.532.171.901.701.531.47

解析要求出电压表的内阻，可通过画图的方法就能很容易地解决问题.可先画出R-1U关系图（如图4所示）.从图像中可看出，图形线与纵坐标轴的截距表示：可变电阻R=0时的电源电压是E=U=3V.再根据欧姆定律可得出电压表的读数U=RVRV+RE，当1U→0时，R→RV，从图中可看出图形线与横坐标轴的交点A 就是电压表的内阻，其值为RV=1000.0Ω.通过利用数形结合的方法，使本题目很容易求出，同时也使求解方法得到创新.

综上所述，要使数形结合思想在高中物理解题中取得良好应用成效，促进学生物理解题能力的提升，需要教师重视数形结合思想在教学中的应用，全面掌握数形结合思想的内涵、特点与要求，掌握数形结合思想在不同类型物理习题中的应用方法，才能加深学生对数形结合思想的理解，促進学生物理解题能力的提升.

参考文献：

[1] 刘笑岩.数形结合思想在高中物理学习中的应用体会[J].考试周刊，2018（4）：95.

[2] 付启甲.数形结合思想在高中物理解题中的应用[J].中学生数理化，2017（1）：46.

[3] 刘丹.数形结合思想在中学物理中的应用[J].科学大众，2012（11）：19-20.

[责任编辑：李璟]