车撞混凝土桥墩精细化建模方法

刘莉萍，刘万锋，郭建博，杜婷，邓锷(1.陇东学院 土木工程学院，甘肃 庆阳 745000；

2.甘肃省高校黄土工程性质及工程应用省级重点实验室，甘肃 庆阳 745000；3.中南大学 土木工程学院，湖南 长沙 410075)

车辆撞击桥梁的事故频发，不仅造成了桥梁结构的损伤，甚至会引起桥梁结构的整体倒塌，造成重大的人员伤亡、巨大的经济损失和恶劣的社会影响。1989年至2000年间发生在美国的503起导致桥梁失效的事故中，车辆撞击占比为11.73%，是导致桥梁失效的第四大原因，远远高于地震、火灾和超载[1]。随着道路交通的发展，仅2020年1月，美国就发生了2起卡车撞击桥梁事故，造成1人死亡；2015年以来纽约州发生了1 100起桥梁被车撞事件；2018年德克萨斯州发生了100起以上桥梁被车撞事件；2002年～2013年间英国发生了19 815起桥梁碰撞事件；我国从2009年至2019年发生了418起运营阶段桥梁倒塌事故，其中车船撞击引起的桥梁坍塌事故高达18.7%[2]。工程设计中一般将桥梁撞击的动态撞击作用简化为等效静力设计值，这种方法未充分考虑桥墩动力响应以及材料应变率效应等因素的影响，且各国规范对车辆撞击力值的规定差异非常大。中国《公路桥涵设计通用规范》规定最大设计撞击力为1 000 kN，而美国桥梁设计规范却高至2 700 kN[3−4]。因此，车桥碰撞的动态求解与设计问题一直备受各国学者关注。过去30年内，试验方法、理论方法与有限元方法是解决车桥碰撞问题的三大主流方法[5−9]。BUTH等[10]进行了2次大型卡车与桥墩的实车碰撞试验，对试验结果进行了分析并且给出了桥墩防撞设计的建议，这些建议后来均被美国桥梁设计规范采用；肖岩等[11]进行了钢管混凝土防撞柱系统实车碰撞试验，获得了卡车与柱状物撞击时卡车前部变形刚度系数及最大撞击力计算公式，并提出了防撞柱的简化设计方法。但是由于足尺试验成本高昂，目前国内外学者开展的足尺碰撞试验较少。而有限元方法由于成本较低，且经过合适的参数选择及模型设置具有较高的求解精度，因此得到了广泛的应用[12−15]。EL-TAWIL等[16]首次采用有限元方法对车辆撞击桥墩进行模拟分析，发现最大碰撞力的作用时间非常短，结构来不及做出反应，因此等效静力比最大撞击力更适用于桥墩防撞设计；SHARMA等[17]采用有限元方法提出了一个基于性能的桥墩防车辆撞击设计方法，定义了损伤水平、撞击水平以及桥墩的剪切承载力和撞击需求；李瑞文等[18]基于LS-DYNA研究了车辆撞击下桥墩的冲击性能和冲击力，提出碰撞荷载经验公式与半正弦荷载时程曲线，用来计算撞击荷载峰值与反应时撞击荷载时程。即使已经有很多学者采用有限元方法研究车桥碰撞问题，但鲜有学者对传统有限元方法提出高精度要求，如解决网格敏感性、永久荷载初始化等问题。为此，本文基于一座高速公路桥梁，建立了完整车辆−桥梁碰撞的有限元模型，并对该模型进行了一系列精度提升工作，主要包括：合理选择接触算法和网格尺寸，以及对重力荷载进行初始化。本研究可为桥梁结构的抗冲击性能研究提供建模思路，以提高开展相似研究的研究效率。

1 车桥碰撞模型

本文所使用的汽车模型是由美国联邦高速公路和美国国家碰撞分析中心(National Crash Analysis Centre,NCAC)推出的F800中型卡车模型。Ford卡车模型净重5.27 t，额定最大重量略小于12 t，模型主要由梁单元、实体单元和壳单元组成。整个汽车模型由35 297个单元和7种材料组成，单元网格划分十分精细，如图1所示。陈林[19]展开的试验与有限元对比研究发现，该卡车模型兼具中型及重型卡车的质量特性，可适用于车撞柱类结构物数值分析。因此本文采用该卡车模型进行车撞桥数值研究。

图1 汽车有限元模型Fig.1 FE model of the vehicle

位于高速公路上的跨线桥往往比其他桥梁遭受更大的被撞风险，此类桥梁若遭遇重型车辆撞击很容易引发交通瘫痪、人员伤亡以及经济损失，因此很有必要对此类桥梁的防撞性能进行研究，从而为防撞设计提供依据。本文以甬金高速公路上一座3×20 m的简支T梁桥为研究对象，桥梁上部结构采用20 m跨径的简支T梁结构，桥面宽7.6 m。下部结构采用双柱式桩柱结构桥墩，桥墩直径1.5 m，墩间距4.0 m，墩高6.3 m，承台尺寸5 m×2 m×0.8 m，墩顶设置6 m×1.2 m盖梁。桥梁整体及各构件尺寸见图2。为提高显式分析的计算效率，采用只有单个积分点的8节点Solid单元模拟桥墩、承台、盖梁、上部结构、桥台和支座。采用Beam梁单元模拟嵌在墩柱中的纵向和横向钢筋。钢筋和混凝土之间的关系假定为完全黏结，采用关键字CONSTRAINED_LAGRANGE_IN_SOLID实现。由于桩土效应对桥墩响应的影响有限，本文模型忽略了桩土效应，并约束桥台及承台各方向自由度。

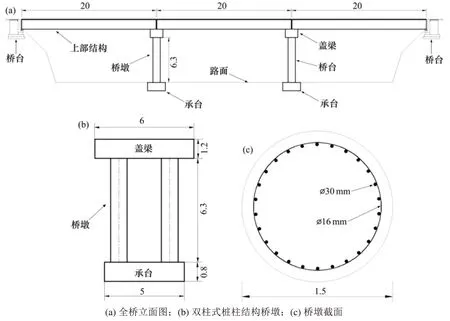
图2 简支T梁桥Fig.2 Simply supported T-shape girder bridge

材料模型选择是决定有限元模拟精度的最重要因素之一，其中最常被用于模拟混凝土材料的模型有混凝土损伤模型(MAT_72R3)、H-J-C模型(MAT_111)以及连续盖帽模型(MAT_159)。其中，混凝土损伤模型在爆炸领域应用广泛，H-J-C模型适用于混凝土材料的冲切、侵蚀分析，这2种模型均不适用于混凝土低速碰撞模拟。连续盖帽模型基于连续损伤力学及塑性理论建立，考虑了材料的硬化、损伤以及应变率效应，被广泛应用于混凝土的碰撞问题模拟中，并展现出了良好的精度。综上所述，本文决定采用连续盖帽模型来模拟混凝土在碰撞作用下的动力性能及损伤特性。

当车辆与桥梁发生碰撞时，车辆本身往往发生剧烈变形，车辆内各部件容易发生随机接触，此时判断车体内各部分的接触面方向变得十分困难。选用自动接触则可以很好地解决该问题，因此，本文车辆-桥梁撞击模型采用自动接触类型。车辆−桥梁碰撞模型的接触类型选择如表1所示。建立好接触关系的完整模型见图3。

表1 接触类型列表Table 1 Types of contact

图3 车辆−桥梁碰撞模型Fig.3 FE model of vehicle-bridge collision

2 车桥碰撞模型验证

如图4为车辆碰撞桥梁的能量转化图，其中分析的能量包括系统的动能、内能、沙漏能以及总能量。在有限元仿真中，沙漏现象的存在会使仿真结果失真，单元严重扭曲时甚至会导致计算终止，所以应该尽量避免和减小。沙漏是一种单元以比结构高得多的频率振动的零能变形模式，是由于单元刚度矩阵秩不足引起的，其直接原因为积分点数量不足。发生沙漏模式的单元通常没有刚度，单元呈现锯齿状变形。通常来说，沙漏能低于结构总能量的5%时可以认为结果是可靠的[20]。如图4所示，系统的沙漏能仅为总能量2.3%，小于5%。因此，可以判定该有限元模型的接触设置及整体模型模拟碰撞是可靠的。同时，车桥碰撞系统应当遵循能量守恒定律，即：车辆在碰撞发生之前具有较高的动能，当与桥墩发生碰撞时，车速降低导致系统动能降低，同时桥墩与车辆变形增大导致内能增大。由图4可知，车辆动能几乎完全转化为桥墩内能和车辆变形内能，车桥碰撞系统符合能量守恒定律。由此可进一步确定有限元模型的正确性。

图4 能量转换时程曲线Fig.4 Energy conversion time-history

对车辆-桥梁碰撞模型进行验证，给车辆施加初速度60 km/h，与桥墩发生正面碰撞。如图5是有限元模拟碰撞结果与事故现场的对比。可以看出，有限元分析与实际碰撞中车辆的变形结果相似，即：碰撞发生时，车辆的车头部分均发生明显的挤压变形。

图5 有限元模拟碰撞事故与事故现场对比Fig.5 Comparison between FE results and real accident

3 模型精细化方法与结果

3.1 网格尺寸选择

在有限元模拟中，网格尺寸的选择是实现计算精度和效率之间良好平衡的关键。首先，网格尺寸需要足够小，以产生收敛的有限元结果。另一方面，由于计算时间和资源的限制，也不能过小。为此，研究了桥墩网格尺寸对结果的影响，本节采用35，50和100 mm 3种不同网格尺寸进行网格敏感性对比。

在初始碰撞速度为60 km/h的车辆碰撞作用下，不同网格尺寸的桥墩损伤云图如图6所示。可以看到，35 mm和50 mm网格桥墩产生的损伤情况比较类似，发生的损伤包括墩底剪切损伤、背面受拉损伤以及墩顶剪切损伤。而采用100 mm网格的桥墩产生的损伤显然比前两者严重。表2是3种不同大小网格的桥墩对应的碰撞力和墩顶位移结果，100 mm网格桥墩产生的碰撞力和最大位移均大于其他2个桥墩。说明网格尺寸较大时容易引起模拟结果产生误差。网格尺寸为35 mm的桥墩与使用50 mm网格的桥墩损伤情况、碰撞力和最大位移均比较接近。因此采用50 mm网格尺寸进行桥墩建模，可达到计算精度和效率之间的平衡。

图6 网格尺寸及损伤结果Fig.6 Damage result of different mesh size

表2 碰撞响应对比Table 2 Comparison of impact response

为进一步确定本文网格尺寸选择的合理性，本节进一步将实际车桥碰撞事故中桥墩损伤特征与有限元结果进行了对比。采用50 mm网格对桥墩进行建模，当车辆速度为80 km/h时的损伤对比结果如图7所示。由图7可知，实际车桥碰撞事故中，桥墩的损伤主要包括墩顶剪切损伤、碰撞位置冲压损伤和背面受拉损伤。如7(b)所示，当有限元模型可以实现以上损伤特征的模拟。综合以上对比结果可以确定，本文采取的有限元精细化建模方法能较好地还原真实事故情况，具有较强的参考价值。

图7 桥墩损伤特征对比Fig.7 Comparison of damage characteristics

3.2 重力荷载初始化

上部结构自重引起的轴向力对桥墩的抗冲击性能有很大影响[21]。在撞击荷载作用下，当桥墩变形较小时，轴向载荷通常能提高桥墩的抗冲击性能。但是，当桥墩变形很大时，轴向荷载的存在可能会引起P-delta效应，从而降低桥墩的轴向承载能力。因此，车辆碰撞有限元模拟都应考虑桥梁结构自重而产生的轴向载荷，并将此作为撞击分析的一部分。

自然状态下，桥墩承受的轴力应为恒定荷载。在本文的桥梁模型中，每根桥墩所承受的轴力为2×103kN，即图8中蓝色线条所代表的轴力数值。然而，LS-DYNA显式分析默认采用无阻尼方法施加重力荷载，且在0时刻将全部重力加载于模型上，相当于对桥梁结构施加了一个瞬时荷载。如图8所示，黑色线条为LS-DYNA默认加载方式下桥墩的轴力图。由图8可见，默认加载方式下的桥墩轴力呈现幅度较大的波动，最大轴力达到了约3.5×103kN，比预期轴力高75%。

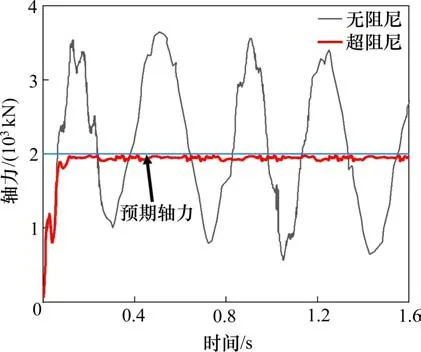
图8 桥墩轴力Fig.8 Axial force of the bridge pier

为防止以上轴力波动的情况发生，可采用dynain文件法、隐式-显式转换法、动力松弛法或超阻尼法进行重力预加载，使轴力接近或等于预期轴力值。以上4种方法中，dynain文件法和隐式-显式转换法都需要从隐式分析转换到显式分析，转换过程中需要手动更改材料应变率设置。当需要处理的模型数量太多时，采用dynain文件法和隐式-显式转换法太过耗时耗力。而动力松弛法则需要花费大量计算时间以达到静力平衡。综上所述，本文采用超阻尼法初始化重力荷载。超阻尼法是在发生碰撞之间，采用关键字*DAMPING_GLOBAL给结构施加一个大于临界阻尼的超阻尼，使得结构快速达到静力平衡。结构达到静力平衡后，将该阻尼删除，然后进行碰撞分析。首先对全桥进行模态分析，得到结构的最小自振频率为ωmin=23.33 rad/s，则结构临界阻尼为D=2ωmin=46.66 rad/s，对结构施加值为1.5D=70 rad/s的超阻尼，施加阻尼的方式见图9。施加阻尼后的桥墩轴力见图8红褐色线条，桥墩轴力在0.2 s时基本达到稳定，即使轴力一直处于波动状态，但整体数值与预期轴力十分接近。

图9 阻尼施加方式Fig.9 Damping-exert method

采用软件默认无阻尼方法和过阻尼方法分别加载重力荷载后，对桥墩进行碰撞分析。车辆速度为60 km/h时的碰撞力及墩顶位移时程曲线如图10和图11。可以看到自重静力平衡对碰撞力的影响很小，这是因为碰撞力的数值主要取决于车辆刚度，而不是桥墩刚度。但墩顶位移受自重静力平衡的影响较大，无阻尼情况下，位移周期比过阻尼法高0.20 s，位移峰值比过阻尼法高1 mm，这再次证明了进行重力初始化的重要性。可见本文采取的重力初始化方法能够在一定程度上消除LS-DYNA软件默认重力加载方式的固有弊端。

图10 碰撞力对比Fig.10 Comparison of the impact force

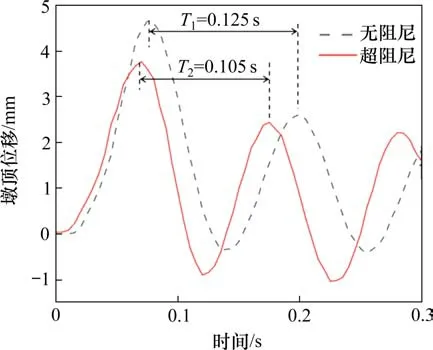
图11 墩顶位移对比Fig.11 Comparison of pier top displacement

4 结论

1)本文采用的精细化建模方法能较好地还原真实事故情况；使用精细化有限元模型模拟的碰撞过程满足能量守恒定律，且系统的沙漏能仅为总能量2.3%，少于5%。因此，可以判定该有限元模型的接触设置及整体模型模拟碰撞时是可靠的。

2)35 mm和50 mm网格桥墩产生的损伤情况、碰撞里结果以及桥墩位移响应结果比较接近。而采用100 mm网格的桥墩产生的损伤显然比前两者严重，且产生的碰撞力和最大位移均大于其他2种网格，结果失真较为严重。可以证明本文选择的50 mm网格尺寸较为合理，达到了计算精度和效率之间的平衡。

3)自重静力平衡对碰撞力的影响很小，但对墩顶位移的影响较大，这证明了在碰撞发生之前先进行重力初始化的必要性。采取的重力初始化方法能够在一定程度上消除ANSYS/LS-DYNA软件的固有弊端。