基于连续变量量子通信的地铁量子调度网络研究

傅思良，李凯迪，于天剑，伍珣

(1.深圳地铁运营集团有限公司，广东 深圳 518040；2.中南大学 交通运输工程学院，湖南 长沙 410075)

地铁调度网络作为地铁运营系统的重要组成部分，是实现地铁系统中列车调度、实时监控和紧急通信等作业顺利进行的基础。近年来，随着国内轨道交通建设的推进和物联网等智能技术的引入[1−3]，地铁调度网络规模日趋扩大，网络数据量攀升，调度通信的信息安全防护也越发受到重视。为保障调度通信系统的数据安全，地铁调度网络亟需高可靠性的保密通信技术。简单来说，保密通信技术指的是发送端Alice和接收端Bob使用密钥对发送的消息分别实行加、解密操作，纵然攻击者Eve拦截了加密的信息也很难将其解密，这样保障了数据安全。现代密码学发展到现在，业界主要提出了对称加密(如DES、AES)、非对称加密(如RSA)、哈希函数(如MD5、SHA-1)和数字签名(如RSA签名)4种加密方法[4]。这些方法的核心思想是加密和解密采用不同的密钥，通过设置复杂的数学问题，用计算的复杂度来保证信息传输的安全性。到目前为止，基于数论的极大整数因数分解难度的RSA公钥加密算法抵御了几乎所有基于现有计算机系统的密码攻击，若选择的密钥够长，它加密的数据将无法破译。然而，随着量子计算(quantum computation)和大规模分布式计算的发展[5]，若量子计算机问世，以RSA为代表的现行主流公钥体制都将会变得不再可靠，将造成极大的安全隐患。首先，量子计算算法的突破将使当前攻击手段更高效。Grover量子算法能将搜索时间降为平方根时间[6]，对私钥(private key)和公钥(public key)密码算法而言，相当于安全密钥被砍掉一半；Shor算法则有能力在多项式时间内解决大整分解和Discrete logarithm问题[7]。更为致命的是，量子计算机一旦成熟，基于公钥体制的身份认证体系会完全失效，Eve可以假冒任意合法设备攻入地铁调度网络。综上所述，地铁调度网络急需寻求一种新型保密通信方案来应对量子计算发展所带来的风险。量子通信是基于量子力学基本原理来实现信息加密的一种突破性保密手段，目的是在合法空间共享实时的、可证安全的密钥，再利用“一次一密”完成无条件安全通信[8]。由于该技术是以量子力学基本原理作为保障，通信双方一旦在信道上成功建立了密钥，就能够在公开信道上进行无条件安全的信息传输，这类具备绝对随机性的密钥从原理上来说无法被攻破，若通信过程被窃听就必然被发现。本文将基于连续变量(continuous-variable，CV)的量子通信技术引入地铁调度网络中，以期借助量子力学基本原理来保证地铁调度网络中的信息安全传输，保障广大乘客人身安全。

1 地铁调度网络

作为地铁运营最重要的组成部分之一，地铁调度网络肩负着地铁系统的列车调度、实时监控和紧急通信等核心职能，是保证地铁安全、集约和高效运营的基础，对保障乘客的乘车舒适性与人身安全具有重要作用。一般来说，地铁每一线路都部署有单独的运营控制中心(OCC)来收集本线路上各个站点及各站点子系统上传的信息(如图1所示)，进行计算处理，最后发出正确的调度指令。

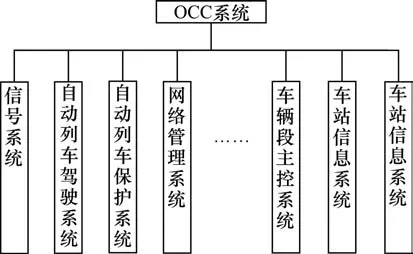
图1 OCC监控的系统Fig.1 Systems monitored by OCC

近年来，为实现多条线路或多个运营商之间的统一调度与科学管理，许多城市开始筹备设立网络运营管理指挥中心，例如深圳地铁建设的位于深云车辆段的网络运营控制中心(NOCC)。NOCC作为整个深圳地铁的“大脑”，获取的参考信息更多、更全面，做出的决策也更加科学先进，但这种集成同时也给地铁调度网络的信息安全提出了更高的需求。一旦NOCC被攻破，所有线路将受到影响，无一幸免。因此，研究信息在地铁调度网络中无条件安全传输将对地铁正常运营以及其在突发事件和重大事故中进行科学决策具有重大意义。

2 量子通信技术

当前，量子信息技术已成为科学前沿的焦点。量子信息技术主要基于纠缠效应[9]，包括量子通信、量子计算、量子传感和量子成像等领域。其中，量子通信领域发展最为成熟。在量子保密通信中，量子密钥和发送的信息经由量子链路和经典链路2条链路传送。密钥采用私钥体制，Alice和Bob双方所持有的密钥是一样的，并且由海森堡测不准原理和不可克隆原理可知[10]，当密钥传输过程中有窃听行为时，Alice和Bob可以发现并且弃用该密钥，从而保证了密钥的安全性。

量子通信最核心的环节是在量子链路上进行的量子密钥分发(quantum key distribution,QKD)。从实现机理的角度来划分，QKD可分为离散变量(discrete-variable,DV)QKD和CV-QKD[8]。前者是利用量子态在希尔伯特空间表示下的离散变量作为信息载体，如单光子的偏振，来进行编码和密钥分发，接收端采用单光子探测器进行检测；而CV-QKD则是利用希尔伯特空间表示下的连续变量进行密钥分发，在接收端则采用平衡零差检测(homodyne detector)或平衡外差检测(heterodyne detector)来提取密钥信息。

2.1 离散变量量子密钥分发

1984年，首个DV-QKD协议由美国IBM的科学家C.H.Bennett和加拿大的密码学家G.Brassard提出，这也是首个QKD协议，简称BB84协议，但QKD协议并没有就此引起业界的关注。直至1991年，应用EPR纠缠态实行密钥分发的协议被Artur Ekert提出，QKD才开始蓬勃发展[11]。目前，基于单光子载体的DV-QKD技术在安全性证明方面已十分成熟，但其实际推广还面临一些局限性。一是单光子难以完美制备及储存；二是单光子信号较弱，单光子探测器的造价十分昂贵，并且探测效率不高；三是在实际工程中，需要在原有的光纤链路以外单独铺设量子链路，这给DV-QKD技术在地铁调度网络中的建设与应用带来了困难。

2.2 连续变量量子密钥分发

不同于DV-QKD技术，CV-QKD在变化值范围是连续的物理量上加载信息，比如相空间表征(动量和位置)，或者量子斯托克斯量[8]。CV-QKD能充分利用已有光纤信道实现共纤传输，很好地融合于现有光通信系统中，无需额外铺设量子链路；一次编码可输出多个密钥比特，密钥成码率高，可实现高速量子保密系统，能适应地铁调度系统日益增长的数据需求。此外，该技术所需器件与经典相干光通信具有良好技术融合性和无缝衔接性，易于产业化。因此，本文拟采用CV-QKD技术对地铁调度网络实施数据保护。

2.2.1 GG02协议

自澳大利亚昆士兰大学的T.C.Ralph教授于1999年首次提出CV-QKD概念至今，20余年时间里，CV-QKD技术已发展、衍生出多种协议，较为经典的协议有高斯调制协议、离散调制协议和压缩态协议等[8]。本文拟采用发展最为成熟的高斯调制协议，即GG02协议，来进行地铁量子调度网络设计。GG02协议由法国的F.GROSSHANS等于2002年提出[12]，该协议(如图2所示)设计了使用弱相干态和相干检测的方案，将发送的量子态映射到服从高斯分布的相干态上，然后由接收者进行检测获取信息，测量得到的信息经过对基、信息协商、隐私放大之后将共享一串安全密钥。该协议使用普通的相干光源作为量子光源，利用标准化的光通信设备实现协议方案。在安全性方面，该协议无条件安全已被彻底证明[8]。

图2 GG02协议基本框图Fig.2 Structure of the GG02 protocol

下面对高斯调制的数理过程进行简要概述。Alice制备正交分量为x(位置)和p(动量)的相干态，其中正交分量x和p可用2个独立同分布的随机变量X和P来表示，且X和P服从相同的均值为0的正态分布(高斯分布)

为了传输一串密钥，发端需制备对应的相干态，即

满足一般的特征值等式

根据上述推导可得出，正则算符̂和̂的方差与Vm之间的关系如下：

2.2.2 安全性分析

上一小节对GG02协议的描述基于制备-测量方案(prepare-and-measure,PM)，这也是在实际应用中采用的方案。而在对协议进行安全性分析，或者说是安全密钥率计算时，往往采用与PM方案等效的纠缠方案(entanglement-based,EB)，这是因为EB方案有利于简化理论分析[13]。EB方案架构可参考图3，图中BS代表50∶50光分束器。Alice端对留在本地的模A进行外差检测的EB方案相当于PM方案中Alice端制备相干态的情形。图3中，Alice首先制备EPR态，该量子态于数学上可以用其协方差矩阵表征：

图3 GG02协议EB方案Fig.3 Entanglement-based scheme of GG02 protocol

其中：T为信道透过率；ϵ为过噪声。除了信道损耗，接收端的量子检测效率和电噪声也将削弱系统性能。最终，系统的总噪声可表示为

式中：χline=1/T-1+ϵ，χh的大小与Bob是部署零差检测还是外差检测有关，当Bob部署零差检测时，这个参数有

式中：η为接收端的量子检测效率；vel为接收端的电噪声，单位也为SNU。当接收端采用外差检测时，χh变为

在不考虑有限码长效应，即渐近情况下，基于反向信息协商的GG02协议密钥率计算公式如下[14]：

式中：β表示协商效率，表示RAB通信双方Alice和Bob的互信息量；RBE表示Eve窃得的信息量。利用公式(7)，2个合法通信方在接收端采用零差检测时的互信息量为

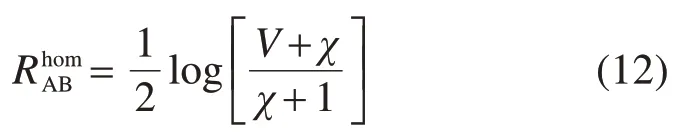
在Bob部署外差检测时的值为

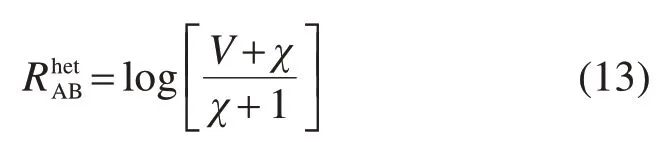
可以看出RhetAB是RhomAB的2倍。Eve获取的信息量RBE则与其攻击方式有关。这里考虑Eve进行集体攻击，其窃得的信息量可用Holevo界表示，计算如下：

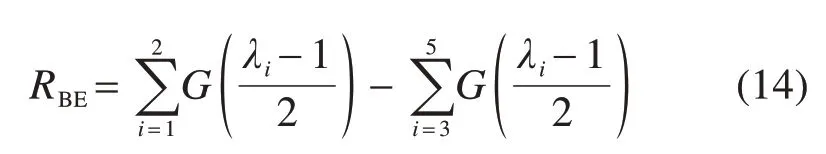
式中：G(x)=(x+1)log(x+1)-x log(x)，上式中辛特征值λ1，2的值为

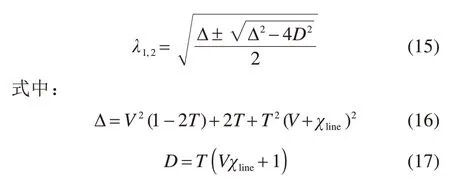
在反向协商的方案中，Eve获取的信息量来自于Bob的测量结果。因此，辛特征值λ3，4的计算如下：

最后一个辛特征值λ5=1。根据式(11)～(22)可以算出集体攻击下高斯调制协议的密钥率的理论值。注意，以上分析采用的协商方式是反向协商方式，这是因为反向协商方式相比于以Alice数据为基准的正向协商方式应对信道衰减的鲁棒性更强[12]。

3 基于CV-QKD技术的地铁量子调度网络

本节以深圳地铁10号线为目标线路考虑量子调度网络设计。深圳地铁10号线，也称“坂田线”，是深圳市轨道交通3期工程项目，始发站位于福田口岸，终点在双拥街，全长29.3 km，共有24座车站。该线的DCC(车场控制中心)控制中心设置在凉帽山站车辆段，与NOCC的直线距离为16 km。在接收到NOCC的调度指令后，凉帽山站车辆段将调度信息转发至全线其余23个站点或指定某站点，从而完成全线的统一指挥调度。

3.1 方案设计

为保证调度信息在传输过程中的安全性，针对10号线NOCC-控制中心-站点的调度布局方式，本文拟采用星型组网方式对CV-QKD设备进行部署，如图4所示。凉帽山站车辆段作为Alice方持有CV-QKD系统的发送端，其余站点则作为Bob端安装接收端设备，当调度指令需要传递到10号线任一指定站点时，凉帽山站车辆段的发送端设备与指定站点的接收端设备同时启用，开始生成、共享量子密钥，并将NOCC传来的指令做加密传输。此种设计相当于将多条点对点线路的发送端进行多合一处理，能大幅节约系统成本，但同时也增加了凉帽山站车辆段的数据计算量。因此，该种组网方式需要在凉帽山站车辆段增加额外的光量子交换机和后处理器。

图4 CV-QKD设备部署示意图Fig.4 Deployment of CV-QKD equipments

在机房布置方面(如图5所示)，CV-QKD设备通过增量部署在原经典网络，只需于原有网络结构上通过密集波分复用技术，占用1个波道，就可以使得量子安全增强业务和经典业务完全互不影响。此外，CV-QKD无需单独部署光纤量子链路，从而极大地节省时间、人力及光纤资源；增量部署的另一个优势在于，即使遇到突发状况、在CVQKD设备未工作的情况下，经典业务的正常运行也不会受到影响。

图5 机房部署示意图Fig.5 Deployment of equipments in communication room

3.2 性能分析

下面对CV-QKD在地铁调度网络中应用的性能进行仿真分析，以验证其可行性。这里关注2个具有代表性的站点，福田口岸站和甘坑站。前者为10号线的终点站，根据深圳地铁10号线正线线路图，该站与凉帽山站车辆段之间的通信线路为21.461 km，是10号线所有站点中与凉帽山站车辆段通信距离最长的站点；后者甘坑站则是与凉帽山站车辆段距离最短的站点，通信距离为1.307 km。在信道损耗方面，深圳地铁10号线调度网部署的是Corning公司SMF-28型单模光纤，该光纤的损耗指标为0.2 dB/km。除信道损耗参数外，本文使用的CV-QKD系统参数如表1所示，所有数值均为实际实验测得或在学术论文中普遍采用的值。

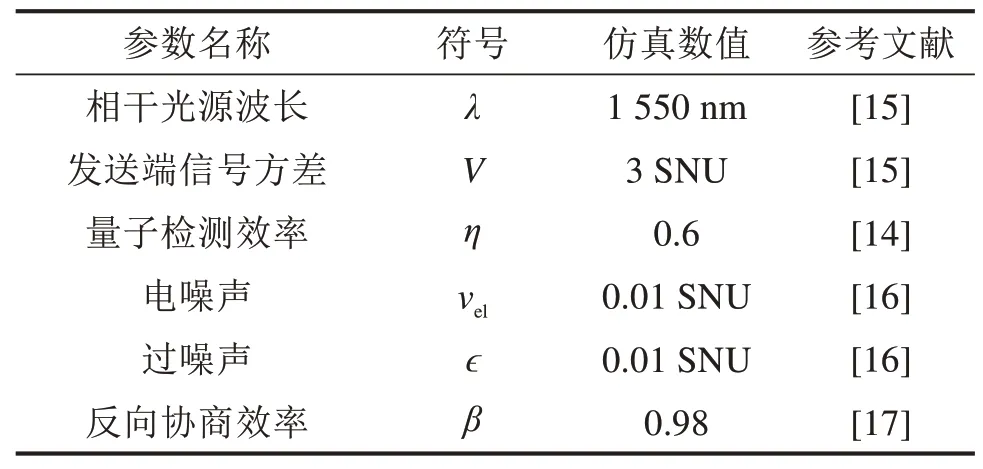
表1 系统参数Table 1 Parameters setting for performance analysis

3.2.1 传输距离

首先验证GG02协议能否满足10号线全线的通信需求。为此，计算在表1参数下GG02协议的安全密钥率与通信距离之间的关系，如图6所示。这里，根据10号线的实际情况，将仿真距离设置为0～25 km。此外，凉帽山站车辆段与福田口岸站、甘坑站通信所能达到的安全密钥率在图中进行了单独标注。本文仿真同时考虑了2种相干检测方式，除安全密钥率曲线外，在图中还给出了QKD技术的PLOB界[18]，该界定义了QKD技术理论上所能达到的安全密钥率上限。从图中可以看出，GG02协议能满足凉帽山站车辆段至10号线全线所有站点之间的通信需求。在通信距离较短的情况下，接收端采用外差检测的方案生成的安全密钥率更高，也就是说在甘坑站可优先选择外差检测方式进行相干检测；随着通信距离的增长，2种检测方案的安全密钥率曲线趋于重合，从成本的角度来说，选择零差检测是一种更经济的方案。同时也看到，2种方案与PLOB界之间有明显的距离，这也意味着方案还有很大的改良空间。事实上，CV-QKD性能的改良有多种途径。一种途径是通过优化表1中的各项参数来提升安全密钥率，这一方式将在下一小节中进行讨论。二是可以采用对信道衰减容忍度更高的协议，如离散调制协议[19]和压缩态协议[20]等，但这些协议目前均不如GG02协议成熟。例如，离散调制协议的安全性证明问题尚未完全解决，这显然无法适用于有着极高安全等级的地铁调度网络。

图6 密钥率与通信距离关系(0～25 km)Fig.6 Secret key rate vs transmission distance(0～25 km)

下面，计算协议在更长通信距离下(大于25 km)的密钥率。上文提到，10号线的运营里程仅有29.3 km。事实上，在深圳地铁中，单线运营里程超过10号线的线路有9条之多。其中，2016年开通的、从福田站开往碧头站的深圳地铁11号线的总运营里程超过了50 km，为目前深圳地铁最长线路。为验证GG02协议能否满足更长线路的保密通信需求，在图7中给出了GG02协议在通信距离超过50 km情况下的安全密钥率。从图中可以看出，GG02协议亦能满足10号线以外更长线路的通信需求。此外，在仿真距离为50～100 km的区间，零差检测和外差检测的安全密钥率曲线基本重合，这说明在这个区间内采用零差检测方式将会是更经济的选择。

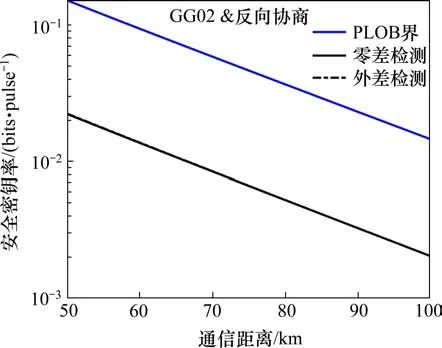
图7 密钥率与通信距离关系(50～100 km)Fig.7 Secret key rate vs transmission distance(50～100 km)

3.2.2 参数优化

在上一小节中指出，通过优化表1中的各项参数，系统的性能可以进一步提升。对表1中的6个参数而言，波长参数采用的是常用的通信波段波长，不对其进行更改；量子检测效率和电噪声与接收端仪器设备的性能质量有关，不在本文的讨论范畴之内；0.98的反向协商效率和0.01的过噪声已是很高的水准，上升空间不大。因此本小节主要考虑对发送端信号方差进行优化。

图8给出了福田口岸站以及甘坑站的安全密钥率与发送端信号方差之间的关系。这里发送端信号方差的仿真区间设置为3～50 SNU。可以看到，2个站点的最优方差存在明显差异。对于甘坑站来说，无论是零差检测还是外差检测，更大的发送端信号方差对系统的安全密钥率更有利。因此在凉帽山站车辆段与甘坑站通信时，应在可允许的范围内使用尽可能大的方差；而在与福田口岸站通信时，凉帽山站车辆段应根据福田口岸站使用的检测方式来确定、调整发送端信号方差。如福田口岸站部署的是零差检测，则应将发送端信号方差调至27.5 SNU以使得系统的性能达到最优，此时的安全密钥率为0.159 1 bit/pulse，比起方差为3 SNU的情况提升了0.060 0 bit/pulse；若福田口岸站采用的是外差检测，则此时系统的最优方差将降至18.2 SNU，对应的安全密钥率为0.158 8 bit/pulse，比起方差为3 SNU的情况提升了0.056 0 bit/pulse。

图8 安全密钥率与发送端信号方差关系(3～50 SNU)Fig.8 Secret key rate vs variance(3～50 SNU)

4 结论

1)基于GG02协议的连续变量量子保密通信方案能满足深圳地铁10号线全线的调度数据保密传输需求，并且有能力实现更远通信距离(更长线路)的调度信息安全传输。该方案与经典业务互不影响，无需要单独部署光纤量子链路，能极大地节省时间、人力及光纤资源。

2)在通信距离较短的情况下，若开销允许，可选择外差检测作为接收端的相干检测方式来提高系统的安全密钥率；此外，在可允许的范围内，短距离通信可通过增大发送端信号方差来进一步提升系统的安全密钥率。

3)在通信距离较长时，发送端优先部署零差检测进行相干检测；在发送端信号方差优化方面，长距离通信存在一个最优的方差值使得安全密钥率达到最大，这个值的大小与接收端采用零差检测还是外差检测有关。