基于PSO−BP−PID单点混合悬浮球控制算法研究
彭月,苏芷玄,杨杰,姜桥
(1.江西理工大学 永磁磁浮技术与轨道交通研究院,江西 赣州 341000;2.江西省磁悬浮技术重点实验室,江西 赣州 341000;3.中铁高新工业股份有限公司,北京 100000)
目前,发展磁浮交通行业不仅能够促进交通技术进步、优化交通结构、解决城市交通运输的问题,还对我国现代化进程产生巨大的推动作用[1]。磁悬浮列车可以简要分为电磁悬浮[2]、电动悬浮[3]、钉扎悬浮[4]和永磁悬浮[5]四大类。其中常导电磁悬浮(EMS)以德国TR系列和日本的HSST[6]为代表。而国内对于磁悬浮技术的相关研究起步较晚,但发展迅速,2016年长沙磁浮快线正式通车[7],2017年北京S1磁浮专线[8]也已正式运营。2019年,时速600 km的高速磁浮实验样车在青岛顺利下线[9],体现了中国磁悬浮技术的不断发展与进步。通过结合电磁与永磁的混合悬浮方式,能够发挥永磁体材料的悬浮性能优势来解决电磁悬浮存在的悬浮能耗大和运行成本高等缺点。国外早在1989年,MORISHITA等[10]就证明了引入永磁结构能够实现悬浮零耗能的可行性,而永磁体的引入也增加了系统的控制难度,对于混合悬浮的控制方法上的研究变得尤为重要[11]。就单点电磁悬浮结构而言,国内外研究者已经对其构建的数学模型进行了算法仿真验证和研究,得出了多种不同的控制策略:KUO等[12]在传统滑模模糊控制基础上针对该模型设计了一种新型控制策略;郑安荣[13]设计了一套复合自抗扰控制器用于改善非线性系统的控制性能;SHAO等[14]设计了指数趋近律滑模控制器,使得控制系统具备良好的跟踪性能;龙鑫林等[15]引入电磁阻尼器,用于非线性反馈控制方法,避免了混合悬浮系统出现磁轨撞击等风险;陈树文[16]提出一种新型滑模控制趋近律对混合系统进行控制仿真实验,证明了该算法具有收敛速度快、无电流抖振的优点。粒子群优化算法自提出以来经历了许多的变化和改进,国内外在关于优化BP-PID算法并应用在非线性的复杂系统上也有不少研究:CLERC等[17]对PSO的粒子迭代公式进行了分析,得出独立粒子的收敛条件;TRELEA[18]对PSO算法的粒子动态表现和收敛条件进行了分析,并提供了相关参数的设置知道规则;JIAO等[19]提出了一种动态变化的权重调节方法;欧青立等[20]利用粒子群算法对BP-PID算法进行优化后应用于注塑机液压系统的控制,可以有效提高该系统的控制精度和响应速度;李强等[21]提出基于粒子群算法优化BP-PID控制的碾米机组控制系统,试验表明经过优化后的控制系统响应速度更快,稳态精度有所提高;龚事引等 采用粒子群算法对模糊控制器量化因子优化并在电磁悬浮球系统进行控制研究,验证该算法有效提高系统的响应速度。本文以江西理工大学自主研发的新型永磁磁浮轨道交通系统——“红轨”[23−25]为背景,研究一种融合PSO与BP-PID的混合型控制算法,该算法利用PSO算法优化神经网络的初始权值问题,来提升算法的收敛速度和精度,填补了传统PID算法响应速度慢以及BP-PID算法收敛速度慢、易陷入局部极值的不足。单点混合悬浮球系统作为混合悬浮列车理想化后的简化模型,对其模型的控制算法的研究可作为磁悬浮列车应用的理论基础,且对于混合磁悬浮技术的学术研究及工程应用提供一定的参考和借鉴意义。
1 单点混合悬浮球系统数学建模
磁悬浮球系统作为研究磁悬浮技术的一种典型单自由度系统,只需要对通入电磁铁的电流施加控制即可实现磁悬浮球的稳定悬浮。该系统借助永磁体的静磁力来实现对悬浮球自身重力的平衡,而电磁系统对悬浮球施加的电磁力发挥悬浮稳定性的调节作用。
在构建该混合系统的被控模型时,做出了如下的假设:
1)不考虑漏磁通,磁通全部通过悬浮球;
2)悬浮球与电磁铁芯材料的磁导率为无穷大,系统的磁场势能均匀的分布在系统的悬浮间隙和永磁体上,即忽略边缘效应;
3)悬浮球受力分析时忽略其他的干扰力。
图2所示物理模型的各符号参数定义如下:电磁铁中的线圈匝数为N,线圈电压为u(t),电流为i(t),铁芯半径为r;永磁体的厚度为hpm,半径为rpm,矫顽力为Hc,磁导率为μ;悬浮间隙为x(t),悬浮球质量为m,重力加速度为g;且可得铁芯的截面积为Spm,永磁体的截面积为S。在上述假设条件下,可得悬浮球的动力学方程为:

图2 混合磁悬浮球系统模型Fig.2 Hybrid magnetic levitation ball system

式中:x(t)为悬浮间隙,以磁极面为零点;F(i,x)为电磁吸力;fd(t)为小球所受干扰力。
图3混合悬浮球系统的等效磁路模型中,各符号所代表的含义如下:
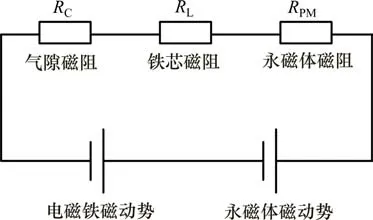
图3 混合磁悬浮球系统的磁路模型Fig.3 Magnetic circuit model of hybrid magnetic levitation ball system
气隙磁阻为Rc=2x(t)μ0S,铁芯磁阻为Rl=L/μS,永磁体磁阻为Rpm=hpm/μ0μrSpm,电磁铁的磁动势为u=Ni(t),永磁体的磁动势为upm=Hchpm。其中,μ0为空气的磁导率,μr为永磁体的相对磁导率,μ为铁芯的磁导率。
由系统的等效磁路模型,可根据磁路的基尔霍夫定律列出该模型的数学公式如下:

悬浮球受到的电磁吸力由电磁铁与永磁体共同作用而产生的合力,在t时刻,瞬时电磁吸力的合力F(i,x)为:

对于电磁铁来说,由基尔霍夫电路定律可以得出电磁铁绕组的电压方程:

式中,Li是悬浮气隙为x(t)时刻的线圈电感。
根据上述的数学推导,可以得到混合磁悬浮球系统的动态数学模型如下所示:
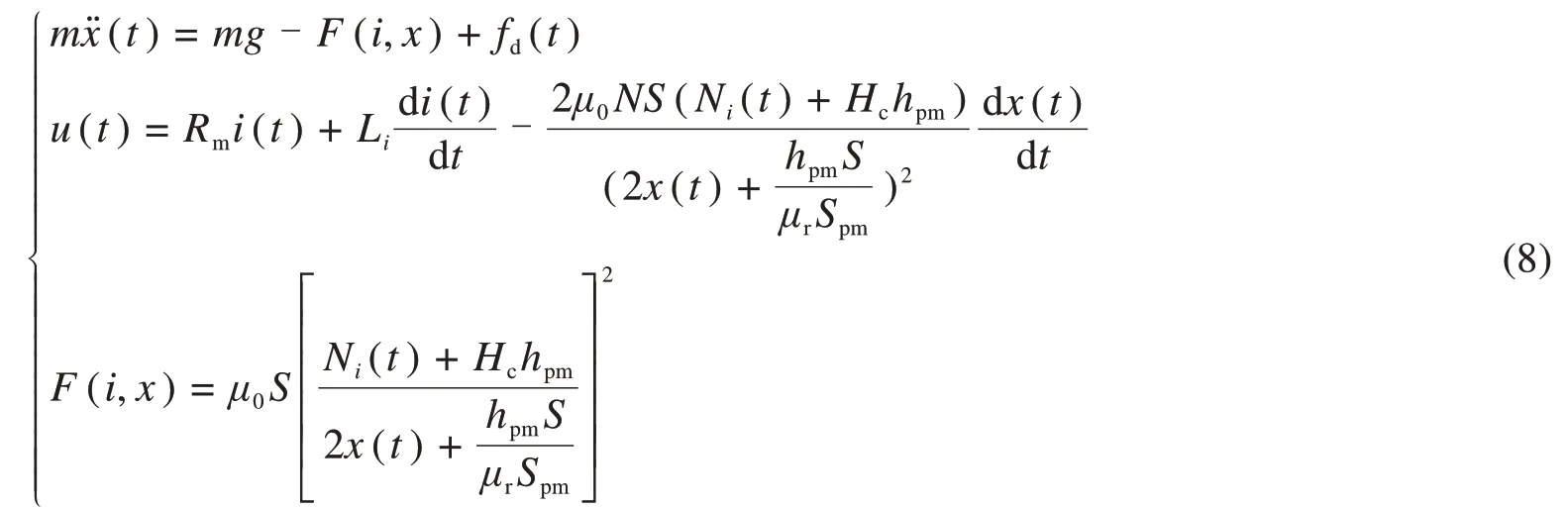
当系统处于平衡点处时,则设平衡时的电流与悬浮气隙为(i0,x0),那系统的边界条件为:

那么原混合磁悬浮球的动态模型经过线性化处理后,可表示为:
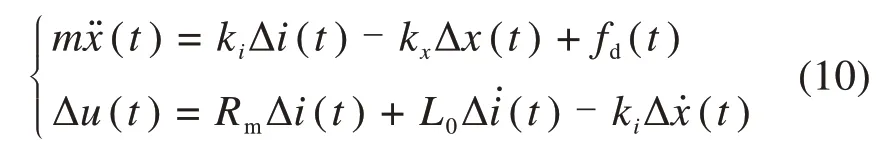

而kx则是悬浮气隙项系数为:
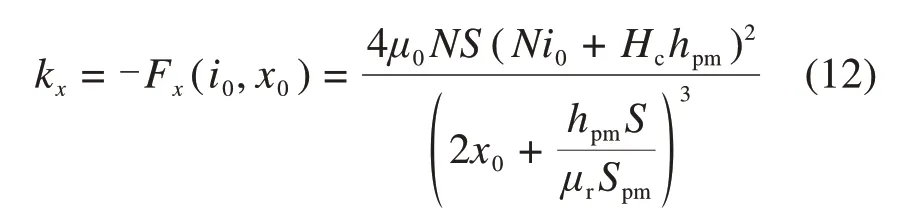
取(Δx,Δẋ,Δi)T作为状态变量,电磁铁两端电压作为输入变量,可将上述方程转换为如下状态空间方程组:
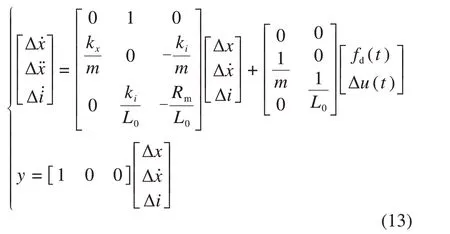
由状态空间方程可得系统的特征方程为:
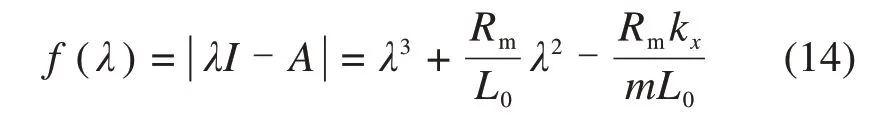
特征方程中的系数出现了负值,根据劳斯判据可以判定该系统是不稳定的。进一步分析可得系统的能控阵M和能观阵N:

能控阵M和能观阵N的秩均为满秩,故系统本身是可控可观的,因而可以通过状态反馈控制使系统达到稳定。
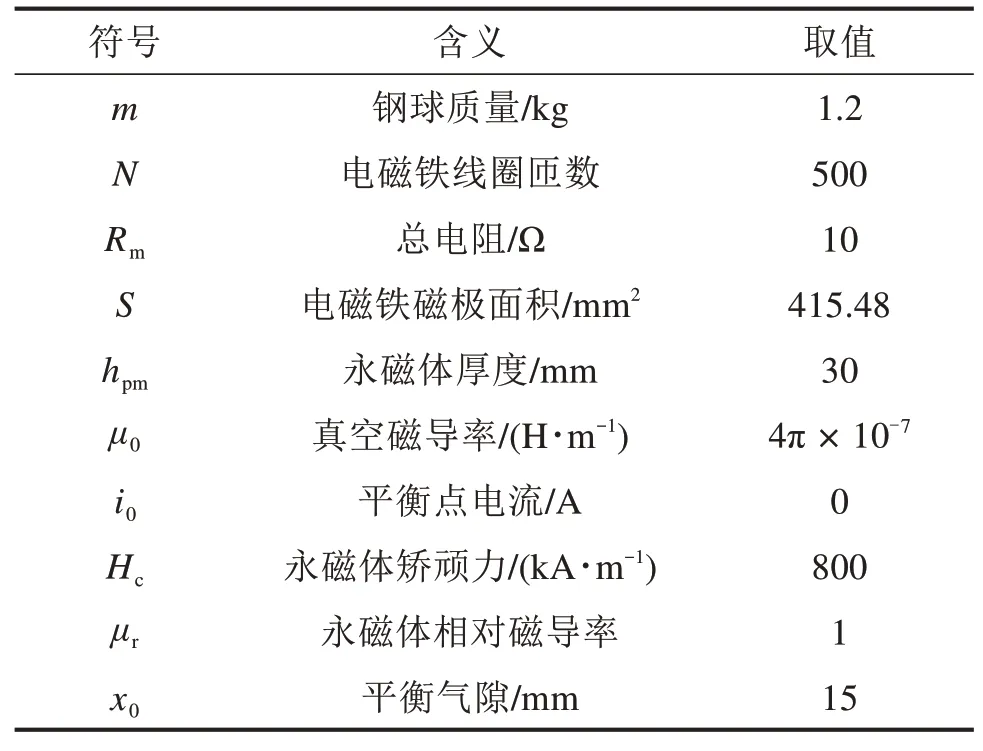
表1 混合磁悬浮球的物理参数Table 1 Physical parameters of hybrid magnetic levitation ball
以电压作为输入变量,利用拉普拉斯变化可求得上述状态空间方程转换为传递函数形式:
图片数据包pic_package封装后先存放在PC内存中,利用驱动程序在系统内存开辟两个DMA缓冲区(上位机与硬件板卡直接通信的数据交互区)pdata_buf1和pdata_buf2。

而由ki,kx,L0表达式可知有k2i=kx L0关系,而在一般的情况下,考虑Rm≥L0,那么传递函数模型可近似表示为:
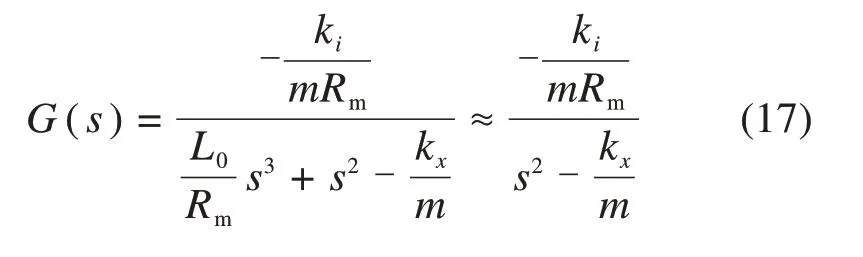
综上可得,混合磁悬浮球模型经过线性化处理后可近似为一个2阶系统。
将物理模型参数代入到传递函数模型中,可得:

2 PSO-BP-PID算法设计
2.1 PSO算法
PSO的原理是通过初始化一群没有质量与体积的粒子,并视每个粒子为优化问题类型的一个可行解,借助设定的适应度函数来评判粒子的好坏[23]。每个粒子设定一个速度变量,来决定粒子在可行解空间中运动的方向与位置,且每经过一次迭代,比较出粒子群中粒子个体的极值与群体极值,并经过不断的迭代,最终得到问题的最优解。粒子在可行解空间中的状态属性设置如下:
假设在一个D维的搜索空间中,存在由M个粒子组成的粒子群体以一定的速度进行飞行,那么在t时刻,粒子群中的粒子i的状态属性设置如下。

Ud分别为搜索空间的下限和上限;

vmin,vmax分别为最小和最大速度;
且1≤d≤D,1≤i≤M。
那么粒子在t+1时刻的速度和位置可以通过下式进行更新得到:
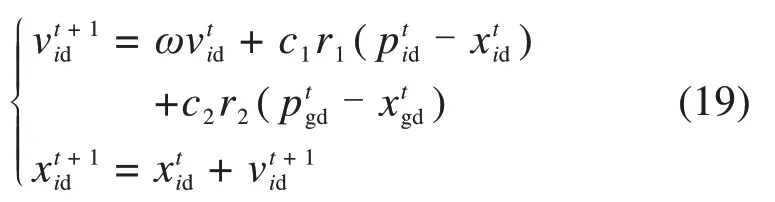
式中:r1和r2为均匀分布在(0,1)区间的随机数;c1和c2为学习因子;ω为权重系数。
2.2 BP-PID算法结构
BP神经网络作为一种使用广泛的反馈网络[26],主要分为3层结构:输入层、隐含层和输出层。BP-PID算法的基本思想是令输出层的3个神经元对应于PID结构中的比例、积分和微分3个参数,借助神经网络的自学习能力,通过调整层与层之间的权重系数来控制PID系数输出。其中BP神经网络的结构如图4所示。
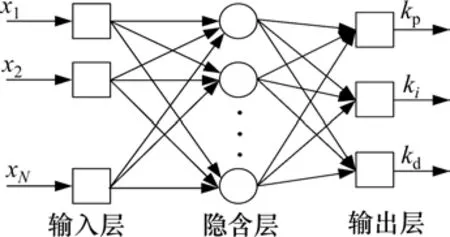
图4 BP神经网络结构Fig.4 BP neural network structure
输出层节点数目是由PID的控制变量参数设置为3个,分别对应PID的3个控制变量。
PID的控制算法采用的是增量式数字PID:

式中:k为采样次数,Kp,Ki和Kd分别是比例系数、积分系数和微分系数。
2.3 PSO-BP-PID算法设计
BP神经网络虽然具备自学能力,能够通过网络训练来寻找到PID参数,但是容易受到初始权值矩阵的影响,造成网络训练收敛速度慢,容易陷入局部最值的缺陷。而粒子群寻优算法则具备能够找到全局最优和收敛速度快的特点,通过将BP神经网络PID算法借助粒子群算法进行优化,那么可以弥补BP神经网络的固有缺陷[27]。
算法流程如图5所示。

图5 粒子群优化BPPID算法流程Fig.5 Particle swarm optimization BPPID algorithm flow chart
3 系统仿真结果分析
根据上述得出的被控函数模型,在MATLAB上利用M函数进行仿真分析,由于该系统是一个非线性的复杂控制对象,将上述得出的被控对象模型进行状态负反馈校正处理后放入至PSO-BPPID算法的M函数中进行离散化。并与传统的PID及BP-PID控制效果进行对比。算法控制器中的采样时间设置为0.01 s,系统的设定悬浮间隙为15 mm;传统PID控制器的3个参数的值选取为Kp=0.027,Ki=0.32,Kd=0.003 439。BP神经网络PID算法的学习率设定为0.5,惯性系数设定为0.03。
图6为经过50次迭代的PSO算法优化后的极值适应度变化曲线。
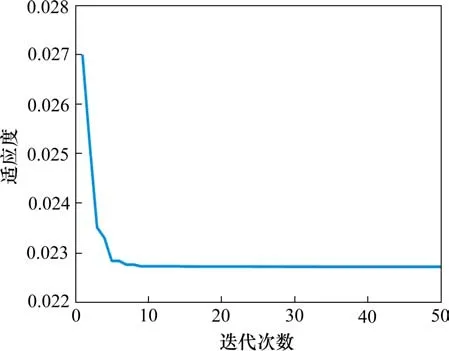
图6 粒子群适应度曲线Fig.6 Particle swarm fitness curve
经过粒子群优化的BP神经网络PID算法的3个参数Kp,Ki和Kd的整定变化如图7所示。
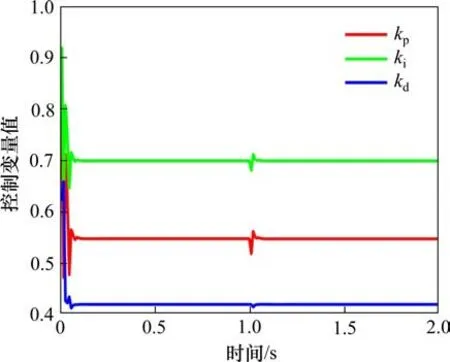
图7 PSO-BP-PID的控制参数整定Fig.7 PSO-BP-PID control parameter tuning
从PID的3个参数的整定变化曲线中可以看出,经过粒子群优化后的BP神经网络能够使得控制参数快速稳定。其中,在1 s时刻模拟系统可能出现的间隙扰动引入脉冲信号,算法的控制参数在出现短暂的突变后便恢复到稳定状态,表现出PSO-BP-PID算法较好的动态自调整能力。
依据系统的平衡点的悬浮间隙为15 mm,在以幅值为15的阶跃信号作为控制器的位置给定下,各算法控制的响应曲线的结果如图8所示。
从图8可以看出,在超调量分析上,传统的PID控制器超调量约7.63%,BP-PID控制器的超调量为0.87%,PSO-BP-PID控制器的超调量为2.28%;在响应时间上,可以看出,PSO-BP-PID响应速度最快,而BP-PID的响应时间长于传统PID控制器。在预设扰动作用下,传统PID控制器出现了3.63%的超调值,而PSO-BP-PID和BP-PID均未出现超调量,且PSO-BP-PID控制下恢复稳定时间比BP-PID算法要快。综合而言,PSO-BP-PID算法在动态性能上表现出了较好的控制效果,具备快速响应与良好的抗扰能力。
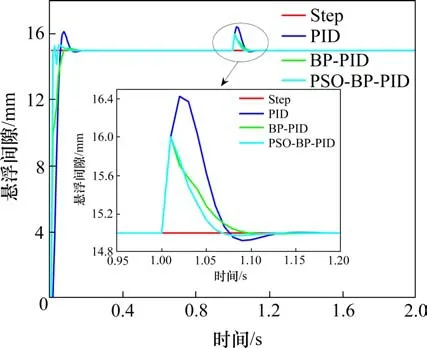
图8 不同控制器下的位置响应Fig.8 Position response under different controllers
为了验证PSO-BP-PID控制器算法的优越性,设计如下的仿真实验:1)控制信号扰动。在1 s和1.5 s时刻分别施加1 mm和2.5 mm的信号脉冲扰动,比较分析不同算法的抗扰动能力;2)间隙扰动。在1 s开始施加幅值为0.5 mm的非线性间隙扰动,观察控制器信号的跟踪性能;3)负载扰动。在1.5 s和2.5 s时施加0.5 s的方波信号模拟负载变化时间隙出现的变化,分析比较不同控制器在负载变化时的控制性能。
1)信号扰动实验
对比图9中控制器的响应曲线,PSO-BP-PID仿真结果的响应速度明显优于BP-PID和传统PID,该算法从出现扰动到恢复到稳定的调节时间也少于其他控制器。分析可知,PSO-BP-PID在抗扰动能力上优于BP-PID和PID算法。
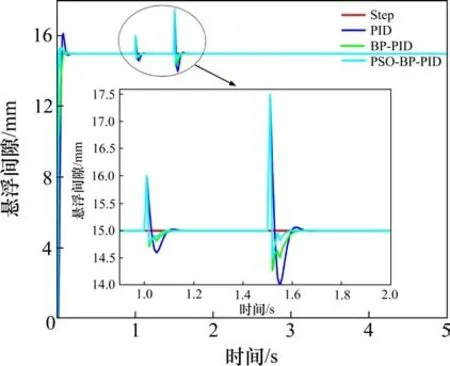
图9 不同控制器下的信号扰动响应Fig.9 Signal disturbance response under different controllers
2)间隙扰动实验
图10的仿真结果表明,在1 s时开始施加非线性扰动时,3种控制器均能够跟踪信号,但相比之下PSO-BP-PID算法可以更快速地跟踪到信号,BP-PID的跟踪性能也优于PID算法,但其跟踪信号的幅值小于信号幅值,说明准确性有所降低。经过PSO优化的BP-PID控制器的跟踪性能相比其他2种更快更准确。

图1 江西理工大学自主研发的永磁悬浮轨道交通系统“红轨”Fig.1“Red Rail”permanent magnet suspension rail transit system developed by Jiangxi University of Science and Technology
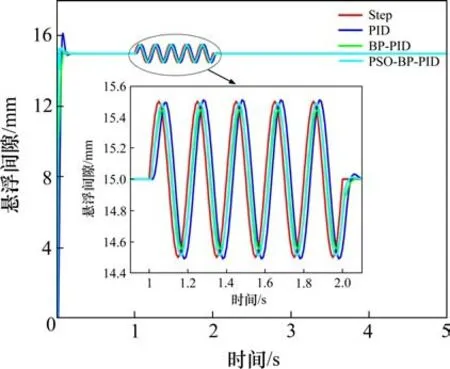
图10 不同控制器下的间隙扰动响应Fig.10 Gap disturbance response under different controllers
3)负载扰动实验
在该实验下,当位置信号出现瞬时跳变时,各控制器均能够做出相应的信号调整。当间隙减小到10 mm时,PSO-BP-PID算法控制器的响应速度最快,且调节时间也最短,而相比PID算法在信号瞬变时出现了较大的超调量,PSO-BP-PID的超调量较小。而当间隙信号增大到20 mm时,PSOBP-PID的各项动态性能指标也优于其他算法控制。通过对比分析可知,在负载出现扰动而导致间隙出现变化时,PSO-BP-PID控制器在不同悬浮间隙下都稳定的跟踪信号,各项的性能指标也优于其他控制器。
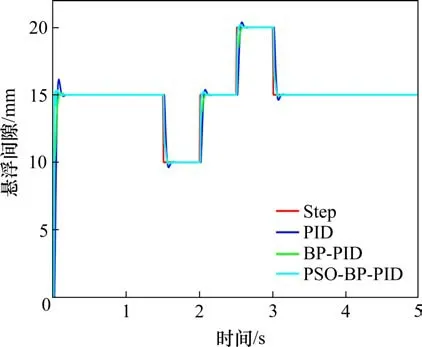
图11 不同控制器的负载扰动响应Fig.11 Load disturbance response of different controllers
4 结论
1)在控制算法上,通过引入PSO算法对网络进行优化,加快了BP神经网络对参数的寻优速率。
2)相比传统PID,PSO-BP-PID在保持较快响应速度的同时;其超调量减少了约70%;在抗扰动性能中,该算法在动态性能上依然具备良好的收敛速率,具备较为明显的控制优势。
3)本文所提控制方法对于磁悬浮轨道交通领域的控制性能提升和节能降耗具有很好的学术意义,也为磁悬浮技术的工程化推广应用提供了很好的基础算法支撑作用。

