高速列车吸能结构开孔设计及结构优化

陈劼昊，梁习锋，许平，车全伟,4

(1.中南大学 交通运输工程学院 教育部轨道交通安全重点实验室，湖南 长沙 410075；2.中南大学 轨道交通安全关键技术国际联合研究实验室，湖南 长沙 410075；3.中南大学 铁道车辆安全技术国家与地方联合工程研究中心，湖南 长沙 410075；4.中车青岛四方股份有限公司，山东 青岛 266111)

吸能结构在列车被动安全保护领域中有着重要的作用，其中薄壁吸能结构以其质量轻、吸能效率高而被广泛应用于吸能结构的设计中。研究人员通过改变结构横截面形状、在结构中进行填充形成复合结构和使用诱导设计等多种方式来提升吸能结构性能[1]。在薄壁结构中引入开孔属于诱导设计中的一种方式，其特点是在吸能结构长度较长时，能够有助于避免结构的整体弯曲，同时在降低结构的初始冲击力上有着明显的效果[2]。许多学者对于开孔结构的力学特性进行了深入的研究，SONG等[3−4]研究了不同大小的方形开孔结构对于方管的吸能特性影响，研究结果显示，在轴向和斜向冲击工况下，孔的大小主要影响结构的初始峰值力，同时，引入开孔设计能够改变结构的变形模式。TRAN等[5]在结构的端部添加了多个圆形孔结构，降低了吸能结构的峰值力。NIKKHAH等[6−7]对结构的水平方向开孔数量和纵向的开孔数量进行研究，结果显示，增加水平方向开孔数量有利于降低峰值力，而纵向上的开孔数量则关系到结构吸能量和变形模式。通过以上文献研究发现，对于开孔设计的研究在开孔形状上更为细致，在对于纵向开孔位置的研究中，学者们大部分采用的方法是，先确定开孔数量，纵向孔与孔之间采用固定距离或者平均分布于结构上，对于合理的开孔距离没有做出更进一步的研究。本文尝试研究通过改变纵向孔之间距离和孔的大小来提高结构的耐撞性能。开孔结构依托于某型号高速动车组前端多胞吸能结构，使用多目标优化设计方法以及代理模型方法对多胞吸能结构的开孔方案进行多目标优化设计，得到合理的纵向开孔分布。在多目标优化设计过程中，引入混合深度代理模型[8]对开孔结构进行多目标优化设计。

1 开孔结构的几何结构和有限元模型

1.1 几何结构说明

如图1所示[9]，以某高速列车的多胞吸能结构作为研究对象，由4个边长为56 mm的正六边形组合而成，4条棱将六边形连接起来，组成一个五胞结构。在六边形和棱连接角度成120°的边上进行圆形开孔设计，图2为初始多胞结构开孔位置的说明，在结构折叠处进行开孔，端部距离第1个开孔位置有半个折叠波长，随后在每一个同侧折叠位置增加一个开孔。本文的研究对象为孔与孔之间的距离，折叠过程中，每个折叠的波长相差不大，因此，将折叠的半波长用变量d表示，第1个孔的位置由1个半波长确定，孔与孔之间的距离则由2个半波长确定。根据试验过程中多胞结构的折叠结果，结构平均折叠波长约为80 mm，因此第1个孔放置在距端部位置40 mm处，随后在下一个同侧折叠位置放置第2个圆形孔，依此类推，2个孔之间的距离为80 mm，初始孔半径设置为r=15 mm。整个结构长度为550 mm，结构厚度为5 mm，由于高速列车吸能结构要求较高的吸能量[10]，在水平方向上设置2个圆形孔，在纵向方向上设置6个圆形孔。

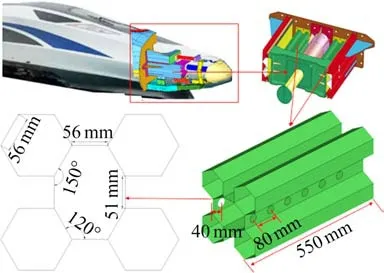
图1 多胞开孔结构Fig.1 Multi-cell windowed structure

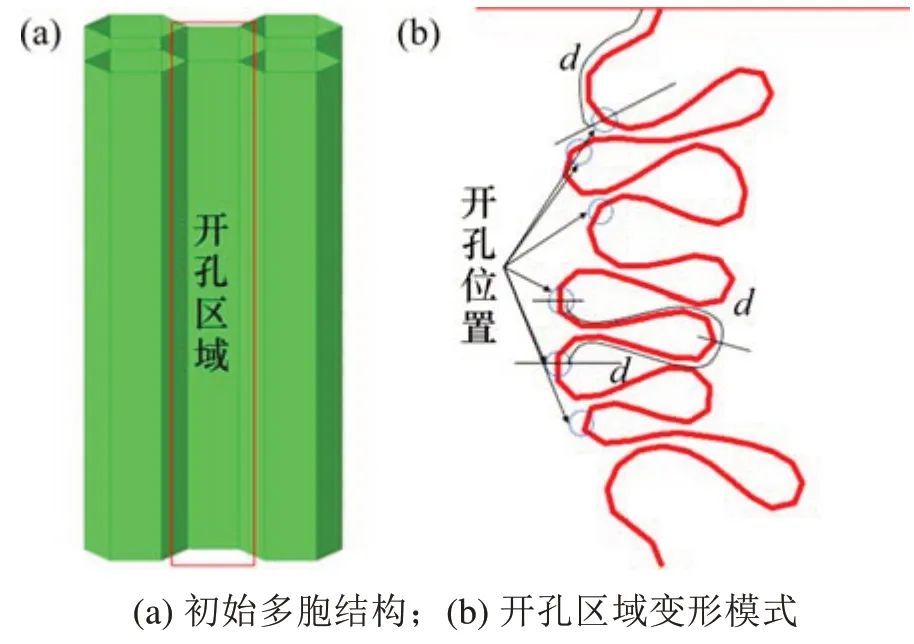
图2 多胞结构开孔位置说明Fig.2 Explanation of window position of multi-cell structure

1.2 有限元模型

本文主要研究开孔多胞结构的冲击行为，使用非线性有限元分析软件LS-DYNA进行数值模拟计算，有限元模型主要由4个部分组成(图3)：多胞开孔吸能结构(图4)、碰撞试验小车、标准轨道和固定刚性墙。吸能结构为6008铝合金材料，为了精确模拟吸能结构的变形，采用5 mm×5 mm[11]的Beltschko-Tsay四边形壳单元对多单元吸能结构进行建模，多胞结构的前后端板采用实体单元进行建模。同时，为了减小计算量，对模型中的试验小车和轨道分别采用30 mm×30 mm和40 mm×40 mm的单元尺寸。吸能结构的接触采用“AUTOMATIC_SINGLE_SURFACE”方法，吸能结构与试验小车、轨道的接触采用“AUTOMATIC_SURFACE_TO_SURFACE”方法，静态摩擦因数定义为0.3，动态摩擦因数定义为0.1[12]，轨道使用全约束，重力加速度设定为9.8 N/kg，试验小车质量为2 t，以指定速度撞击刚性墙。多胞结构的材料参数设置参照文献[9]中的材料参数设置，使用LS_DYNA中的MAT_24来定义多胞结构的材料，其中，密度ρ=2 700 kg/m3，杨氏模量E=72 000 MPa，泊松比μ=0.3，屈服应力σy=131.82 MPa，极限应力σu=190.68 MPa。

图3 多胞结构的有限元模型和边界环境Fig.3 Finite element model boundary conditions and multi-cell structure

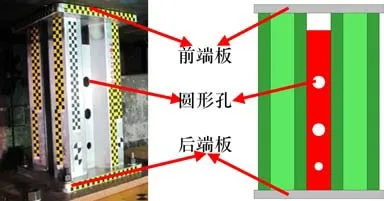
图4 试验验证试件形状Fig.4 Shape of samples used for finite element model validation

1.3 有限元模型的验证

为了验证有限元模型的正确性，使用开孔的多胞结构进行冲击试验。为了保证试验条件与有限元模型相符，将吸能结构通过4个20号螺栓固定在试验台车上，试验台车的设计重量为2 t，大吨位力传感器布置在刚性墙上进行力的采集，试验速度采用红外线测速仪记录。其中测速仪采集到的冲击速度为15.3 m/s。

图5和图6分别显示了试验样品和数值模拟的力时间曲线和变形结果。可以看到，试验和仿真的力时间曲线在关键的位置呈现出相同的变化趋势，并且都产生了5次折叠，变形结果表现出很好的一致性。力时间对比曲线中，仿真曲线的谷值要高于试验曲线的谷值，这是由于试件是由拉伸成型，结构内部存在一定的裂痕，导致曲线存在一定的差异。但是本文中主要的研究对象PCF的试验和仿真结果为分别1 311 kN和1 276 kN，EA的试验和仿真结果分别为235.54 kJ和244.15 kJ，同时，试验和仿真的持续时间分别为39.7 ms和38.5 ms，误差分别为2.67%，3.65%和3.02%，对后续的分析影响较小。因此，本文的有限元模型可以看成是较为精确的模型，可用于进一步研究开孔设计对于多胞结构的影响。

图5 试验和仿真的力时间曲线Fig.5 Crash force-time curves for experimental and simulation

图6 试验和仿真的变形模式对比Fig.6 Comparison of deformation modes between experimental and simulation

2 代理模型构建

2.1 耐撞性指标

高速列车的多胞吸能结构主要通过压缩变形来吸收冲击动能。为了评价薄壁结构的耐撞性能，本文使用以下3个耐撞性指标。

吸能量EA，吸能结构吸收的总能量，是评价吸能结构性能的重要指标，它可以从冲击力-位移曲线中整合，计算方式如式(1)所示：

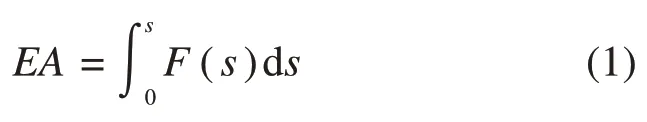
其中：s表示结构压缩时的位移，由于不同结构的压实时位移是不一致的，选择相同的压缩值来计算结构的吸能量是不准确的。本文引入概念—吸能效率(f)[13]来计算结构最大的位移，并将此时的压缩量作为结构最终吸能量。公式定义如下：

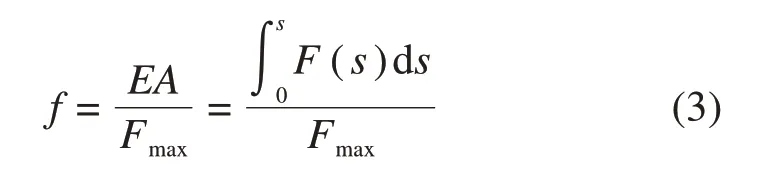
其中：Fmax为结构折叠过程中所产生的除初始峰值力外的最大力。结构在折叠过程中，EA和位移呈近似线性增加，此时f也随着位移增加而增加，当压缩到密实阶段时，压缩力急剧增加，而位移变化很小，此时f会出现极大值，随后f开始下降，因此，当f达到最大值时，认为此时刻结构到达压实阶段，吸能结构的吸能量达到最大。

峰值力PCF，是结构在吸能过程中产生的第1个最大压溃力，结构压缩过程中产生的力值关系到撞击过程中乘员受到的加速度大小，是被动安全保护的重要指标。

比吸能(SEA)，是指薄壁构件单位质量所吸收的能量。SEA计算方法如式(2)所示：

其中：m为吸能结构的总质量。在结构的耐撞性设计中，SEA值反映了吸能结构在吸能方面的利用率，值越大表示结构设计越有效。

2.2 试验设计

本文主要研究开孔位置的分布，以图1中的开孔结构为研究对象，选择结构厚度t，开孔半径r以及开孔位置d3个变量作为优化参数。耐撞性响应与几何参数之间的关系往往比较复杂，难以用数学方法表达。因此，可以使用替代模型来表达这些关系。为了构造精确的模型，通常采用DOE方法在设计空间中选取样本点。在结构耐撞性设计中，以全因子设计、中心复合设计或者拉丁超立方采样方法作为采样方法，都能够得到较为准确的代理模型，本文使用拉丁超立方采样方法选取25个样本点，此外，为了保证代理模型的准确性，应使用另一个矩阵来验证替代模型的精度，通过随机产生9个验证点，样本点和验证点的参数分布情况如图7。

图7 样本点和验证点分布Fig.7 Distribution of sample points and verification points

2.3 混合深度代理模型

采用混合深度代理模型对采样点进行近似拟合。混合深度代理模型是一种组合模型，由基础代理模型和深度信念网络优化2部分组成，首先使用基础代理模型对采样点进行拟合预测，然后通过深度信念网络(DNB)对基础代理模型进行分类和优化，其特点是能够通过输出响应之间的强相关性来优化基础代理模型的精度，而在结构的耐撞性响应中，相互之间的联系较为紧密，符合混合深度代理模型的使用环境。

对于基础代理模型，采用径向基函数(RBF)模型，RBF模型最初是为分散的多元数据插值而开发的，它使用基函数的加权和来逼近高度非线性的输出响应数据[14]。对于由输入变量值和响应值组成的数据集，预测值f(x)可近似为：

其中:m是采样点的数目；x是输入变量的向量；xi是第ith个采样点；||x-xi||是欧氏范数；φ是基函数(高斯、多项式、逆多项式)；λi是基函数的系数。pj(x)是一个低阶(常数或线性)多项式函数，本文使用的是线性多项式函数。RBF的参数根据验证样本点进行自适应[15]获取。

DBN是Hinton在2006年提出的一种基于深度学习技术的神经网络模型[16]。它是多个受限玻耳兹曼机(restricted boltzmann machines，RBM)的叠加，每个RBM只有2层神经元，一层是由可见神经元组成的可见层，用于输入训练数据；另一层是由隐藏神经元组成的隐藏层，用于提取训练数据特征。在RBM中，可见神经元v和隐神经元h通过加权连接，但同一类神经元之间没有联系。bi和ci分别是可见层和隐层神经元的偏向。可见单位和隐藏单位的计算值如式(5)～(6)：

RBM是一种基于能量的模型。不同粒子的概率与其能量成反比，其能量函数E和概率分布模型p被定义为

其中：θ是RBM的训练参数，包括神经元之间的权重w，可见层的偏差b和隐藏层的偏差c。使用式(9)，可视单元的概率计算为p(v)的边际分布，如下所示：

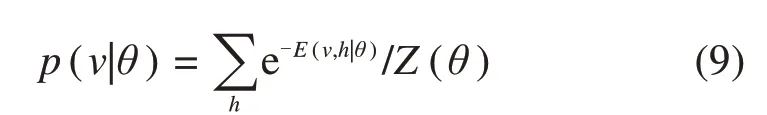
DBN训练的目标是训练DBN中每个RBM的权值和偏差系数。通过对初始输入数据进行重构，降低了能量函数，在参数调整过程中使重构误差最小化。训练过程可以抽象为对数似然函数的概率最大化。

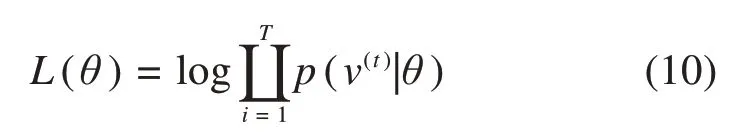
其中：T是样本点的数量。DBN网络模型采用2层RBM结构，学习效率设置为0.001，迭代次数设置为100。

基于拉丁超立方采样的计算结果，结合RBF代理模型和训练出来的DBN深度信念神经网络，形成开孔结构的混合深度代理模型，其训练过程如图8所示。

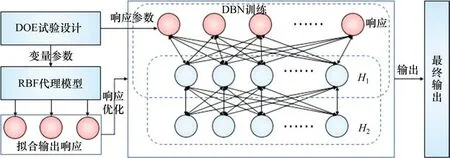
图8 混合深度代理模型训练过程Fig.8 Training process of hybrid surrogate model

2.4 代理模型的误差分析

为了确保代理模型的有效性，采用归一化均方根误差(normalized root mean squared error，NRMSE)、最大相对误差(maximum relative error，MRE)和平均相对误差(average relative error，ARE)3个参数来评价代理模型的精度，计算方法见式(11)～(13)：

其中：n是验证点个数；yi是真实值；̂i是代理模型预测结果；ymax和ymin分别是真实值中的最大值和最小值。

图9显示了RBF模型和混合深度代理模型对于PCF，EA和SEA结果预测的准确性。图中可以看到，DBN-RBF代理模型在EA和SEA中的MRE，ARE和NRMSE均好于RBF代理模型，而对于PCF的预测上，2种代理模型结果相差不大，这是因为RBF模型对PCF预测精度本身就达到了一个很高的精度。使用DBN对这3个变量的内在联系进行挖掘，依靠3个变量之间相互影响对模型进行优化，其中，EA和SEA的精度得到了提高，而PCF在RBF中的误差很小，结果变化不大。总体来说，DBN-RBF混合深度代理模型是能够有效整合耐撞性指标之间的内在联系，提高RBF代理模型的精度，为下一步的耐撞性优化提供更好的结果。

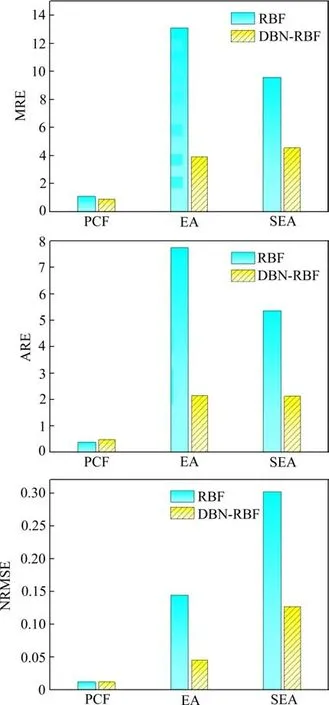
图9 RBF和DBN-RBF精度对比Fig.9 Comparison of RBF model and DBN-RBF with error indexes

3 优化设计

3.1 优化问题描述

结构的耐撞性优化设计是通过改变现有的结构参数来提高结构的吸能特性。在结构的耐撞性指标中，SEA和PCF被视为较为重要的优化目标，因为理想的能量吸收结构是能够以较低的峰值力来吸收较高的能量，因此采用多目标优化方法对开孔结构进行优化设计。文中以图1中开孔结构作为优化对象，孔的半径r，孔的距离d和开孔结构的壁厚t作为优化变量，开孔结构在轴向载荷作用下的多目标优化问题可以表示为：

3.2 优化算法

多目标遗传算法是一种有效的解决多目标优化问题的优化方法。在多目标优化问题中，存在多个要最小化或最大化的目标函数，因此目标不是寻找最优解而是寻找Pareto前沿。因此，在本研究中使用了该算法来求解多目标优化问题的Pareto前沿，参数定义为：最大迭代次数为50，最小迭代次数为25，种群数量为70，非支配点数量为500，变异率为0.01，精英规模为10%。整个优化过程如图10所示。

图10 优化流程Fig.10 Flowchart of multi-objective optimization

3.3 结果和讨论

使用多目标遗传算法得到了开孔结构的耐撞性优化的pareto前沿，其分布如图11所示。图中可以明显看到PCF和SEA两者之间存在着冲突关系，无法同时达到最优的结果。为了选择合适的结果作为优化目标，采用最小距离方法[17]选择满意解，该计算过程如式(15)所示。其中在求解距离之前，对于不同的优化目标，由于其变化范围不一致，为了选择到最满意的解，对2个优化目标的值映射到[0,1]范围内。

图11 耐撞性优化后的开孔结构Pareto前沿Fig.11 Pareto fronts for the crashworthiness optimization of windowed structure

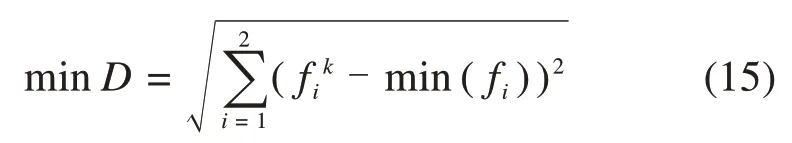
最终，通过最小距离方法选择出来的最佳开孔结构的参数为t=4.78，r=8.37，d=38.37。同时将得到的优化结构进行有限元仿真计算，仿真结果和预测结果见表1。可以看出，误差百分比在可接受的范围内，优化结果符合要求。

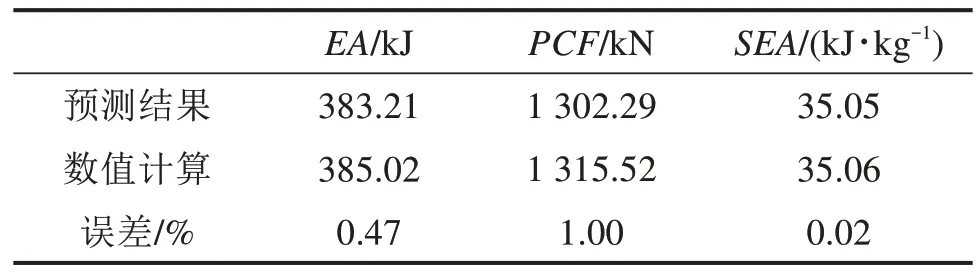
表1 优化方案验证Table 1 Verification of optimal solution

此外，将初始设计的开孔结构、优化后的开孔结构和未开孔的原始多胞结构的耐撞性能进行对比，其耐撞性指标结果如表2所示，初始设计方案和优化后的开孔方案都保证了原始结构的吸能量，而对初始设计方案进行多目标优化后，使结构的PCF从下降3%提高到了下降7%，而SEA从未优化前的2%提升到了6%，因此，采取合理布置吸能结构的开孔位置能够有效地提升吸能结构的耐撞性能。

表2 开孔结构和原始结构对比Table 2 Comparison of windowed structure and original design

4 结论

1)采用开孔方式对高速列车的吸能结构进行优化设计，对吸能结构进行试验和数值仿真计算，结果显示两者吻合度较高，数值仿真计算能有效替代试验结果。

2)使用混合深度网络来构建开孔结构的代理模型，在使用RBF代理模型的基础上，利用各个响应之间的深度联系，使用DNB网络对RBF代理模型优化，结果显示，DBN-RBF模型在针对本文研究的问题上，能够进一步提高RBF代理模型的精度。

3)使用多目标遗传算法对开孔结构的t，r和d进行参数优化设计，得到最后的开孔设计方案，同初始无孔结构相比，开孔结构在保持吸能量的同时，使未开孔结构的PCF降低了7%，同时使SEA提高了6%。