结构不确定性对高速铁路矮塔斜拉桥概率地震需求的影响

谢明志，杨永清，庄重，黄胜前

(1.西南交通大学 土木工程学院，四川 成都 610031；2.成都建工集团有限公司，四川 成都 610000)

矮塔斜拉桥兼具梁式体系桥梁和传统斜拉桥优点，是介于二者之间的组合体系桥梁[1]，其主梁刚度比相似跨度斜拉桥大，同时又比同类型梁桥主梁高度小[2]。当受桥下净空、通航、刚度或美学等方面要求，传统斜拉桥和梁式桥受限时，多采用矮塔斜拉桥，其主跨在150～250 m范围内具有较强的竞争力，近年来在高速铁路桥梁中应用也越来越广泛[3−4]。特别是在中国中西部地区，由于铁路运输发展需求，修建了越来越多的矮塔斜拉桥，其抗震性能也备受关注[5]。开展桥梁结构计算分析时，由于材料参数、几何尺寸和荷载效应等结构不确定性参数影响，将影响有限元模型理论计算值的准确性。与此同时，结构不确定性是桥梁概率地震易损性分析不确定性因素的主要来源之一，对易损性需求参数及概率地震需求分析产生较大影响[6]。谢明志等[4,7]研究表明，参数变化受斜拉桥建造全过程诸多因素影响，如设计、制造加工、施工和环境等，其分布特征及变异系数存在较大不同。因此，需进一步研究结构随机参数对桥梁动力损伤的影响程度，研究各类不确定性参数对高速铁路矮塔斜拉桥概率地震需求分析影响，为易损性分析提供理论依据。吴文朋等[8]考虑材料、边界以及结构等3种模型参数不确定性，以4×30 m的钢筋混凝土连续梁为背景，采用龙卷风法研究不确定性对桥梁地震需求分析敏感性，同时对比分析构件概率地震需求和易损性曲线的关系。宋帅等[9]以3×30 m预应力混凝土连续梁为背景，通过Monte-Carlo抽样法构件样本，引入重要性测度方法，进一步明确参数不确定性对桥梁易损性影响。PADGETT等[10]以一座三跨简支梁为背景，从高效性、充分性及通用性方面，研究结构尺寸、地震波和理论模拟等对桥梁动力响应的影响，得出结构尺寸影响较大。TUBALDI等[11]以一座(40+50+40)m的叠合梁桥为背景，开展不确定性参数对概率地震需求分析的影响，得出模型参数影响较大，不容忽视。上述不确定性研究一方面侧重于公路中小跨度桥梁，另一方面尚未考虑材料参数相关性影响。高速铁路斜拉桥由于构造、受力及动力特性与传统中小跨度公路桥差异大，因此，本文以典型高速铁路矮塔斜拉桥为背景，考虑随机参数相关性，进一步探明结构不确定性对其概率地震需求影响，为复杂桥梁地震易损性分析奠定基础，同时为损伤分析和评估提供科学依据。

1 非线性有限元模型建立

1.1 工程概况

本文以湖南怀邵衡铁路沅江矮塔斜拉桥为背景，其跨径布置为(90+180+90)m的双线铁路单箱单室预应力混凝土矮塔斜拉加劲连续梁桥。主梁及索塔均采用C55混凝土，斜拉索采用1 860 MPa钢绞线，空间双索面布置；C35圆端形桥墩。本桥二期恒载115 kN/m。该桥总体布置及相关信息如图1所示。

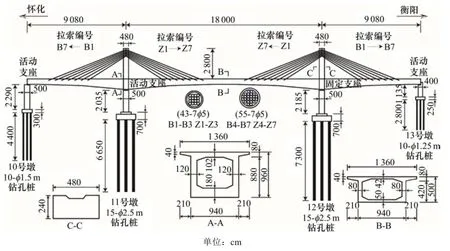
图1 桥梁总体布置图Fig.1 Bridge general layout

1.2 动力有限元模型建立

本桥采用OpenSees开源程序建立非线性有限元模型。斜拉索采用Truss Element，主梁采用DispBeamColumn Element，采用材料分别为Steel02 Material和Elastic Material。索塔、桥墩和桩基础单元均采用NonlinearBeamColumn Element。本桥为塔梁固结形式，索塔与主梁采用刚臂连接。支座按其实际位置进行模拟，每个支座采用“零长度单元”，双节点设置，其中上节点与主梁刚臂连接，下节点与桥墩刚臂连接，支座单元选用Zero-Length Element，采用材料为Elastic-Perfectly Plastic Material。本桥采用“m”法考虑桩土相互作用，沿着桩长方向，用土弹簧模拟其影响。土弹簧采用“零长度单元”，选用ZeroLength Element。本桥构件间的连接刚臂采用Elastic Beam Column Element进行模拟。刚臂及土弹簧材料均为Elastic Material。索塔、桥墩和桩基均采用纤维截面，材料均为Concrete02 Material和Steel02 Material。材料本构关系及支座滞回模型如图2所示。

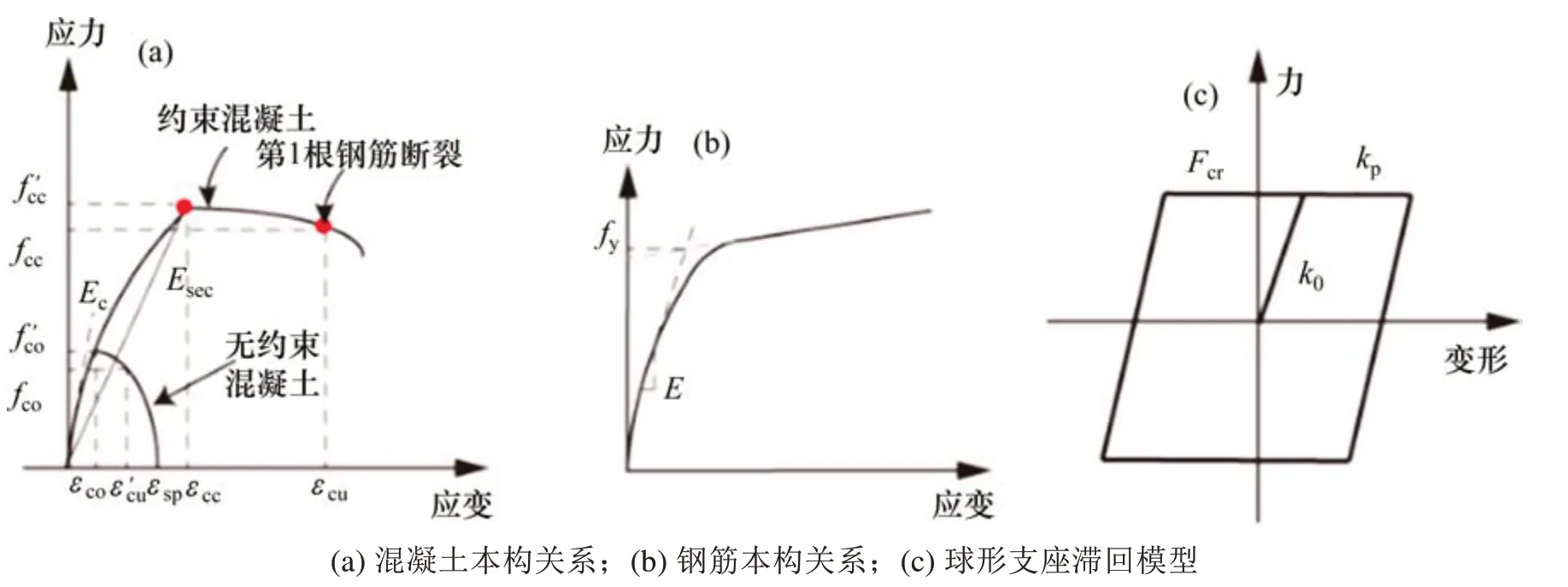
图2 材料本构关系及支座滞回模型Fig.2 Material constitutive relation and bearing hysteretic model

本文研究参数变化对矮塔斜拉桥概率地震需求的影响，对于基准模型各参数取值如下：索塔、桥墩及桩基纤维截面参数取值如表1所示；主梁混凝土弹性模量取36 GPa，斜拉索弹性模量取195 GPa，屈服强度取1 860 MPa，支座摩擦因数取0.02，阻尼比取0.05，钢筋屈服强度为400 MPa，钢筋弹性模量为200 GPa；混凝土容重取26.5 kN/m3。

表1 模型参数取值Table 1 Model parameter value

2 地震波选取

合理地震动数量是不确定性分析需关注的重要问题。过多的地震波显然会增大计算工作量，造成资源浪费，过少则难以反映不确定性。文献[12]针对不同数量地震动作用下，从计算稳定性角度出发，拟合结构损伤指标对数标准差sln(D)与地震动条数的关联性，随着地震动条数的增加，标准差sln(D)趋于稳定。本文按此方法，根据本桥结构特点、区域位置、II类场地和抗震设防等要求，确定适用于本桥易损性分析的目标反应谱，并以均方差最小原则从美国太平洋地震工程研究中心(PEER)中筛选30条地震波，x和y方向加速度反应谱如图3所示。进行非线性时程分析时，将每条地震波从0.1g～1.5g调幅处理，采用增量动力分析方法(Incremental Dynamic Analysis，即IDA方法)进行计算。

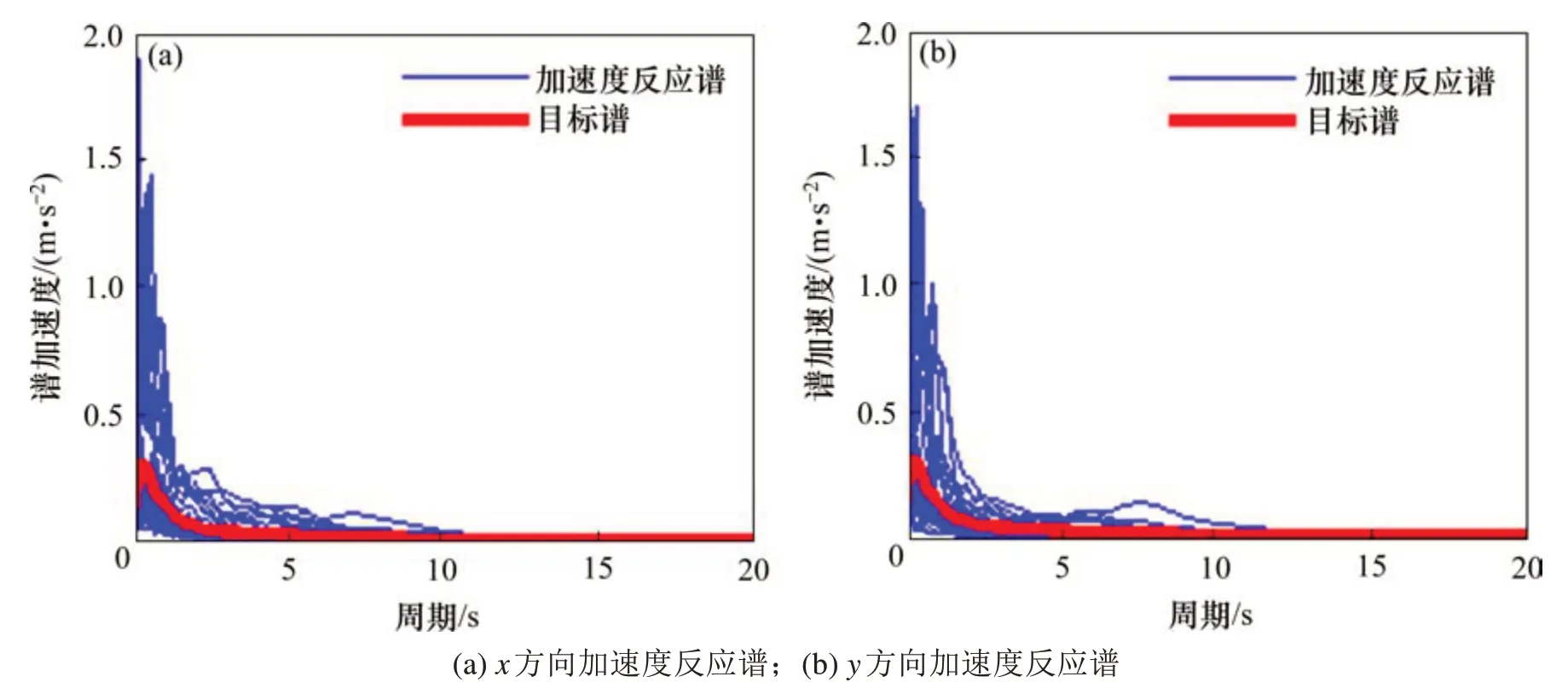
图3 加速度反应谱Fig.3 Acceleration response spectrum

3 结构不确定性

结构不确定性主要源于有限元建模相关参数的不确定性，进而对桥梁动力响应产生影响。因此，对于矮塔斜拉桥，结构不确定性主要考虑：材料、结构几何尺寸、作用及动力学参数。

3.1 随机参数选取及分布

本文在既有研究基础上[6]，综合考虑材料、构件几何尺寸、作用及动力学参数，建立各不确定性参数概率分布模型，如表2所示。采用IDA计算，由于钢筋混凝土纤维截面参数相关性不容忽视，需考虑其相关性影响。本文参阅文献[13]公、铁两用斜拉桥研究结果，混凝土材料参数相关性系数矩阵如表3所示。

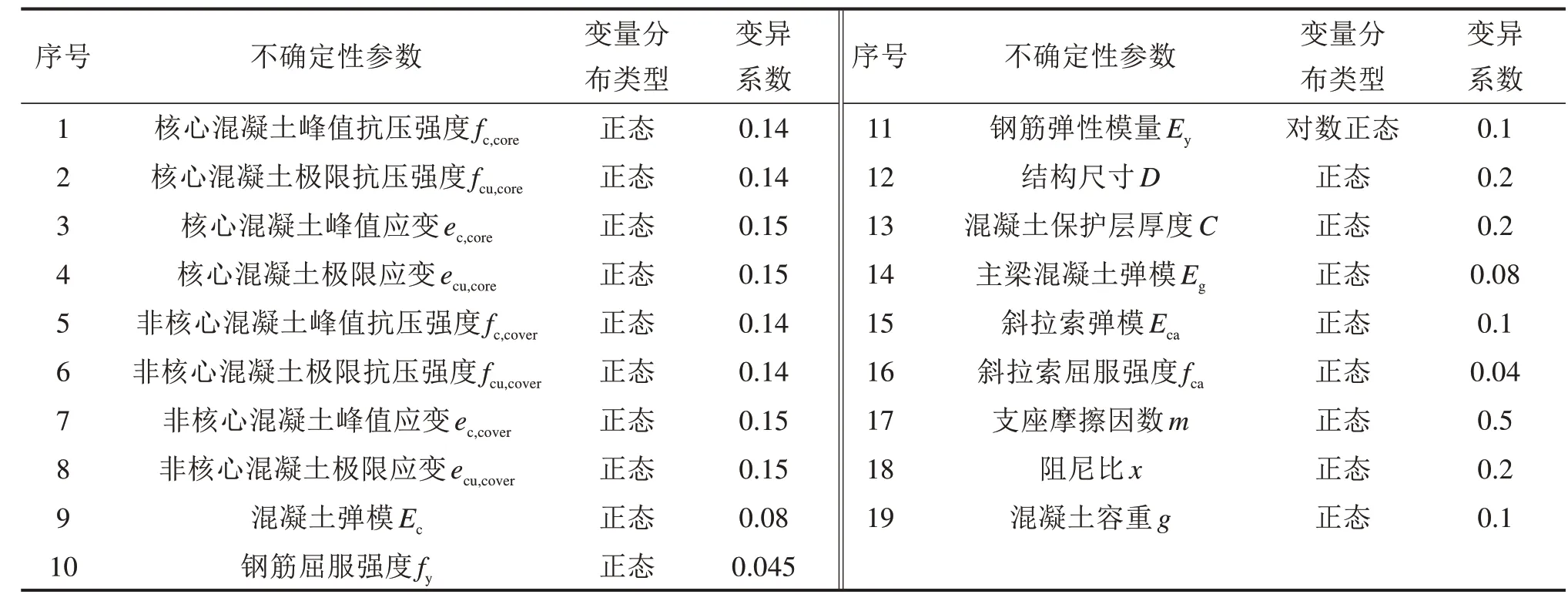
表2 不确定性参数概率分布Table 2 Probability distribution of uncertainty parameters

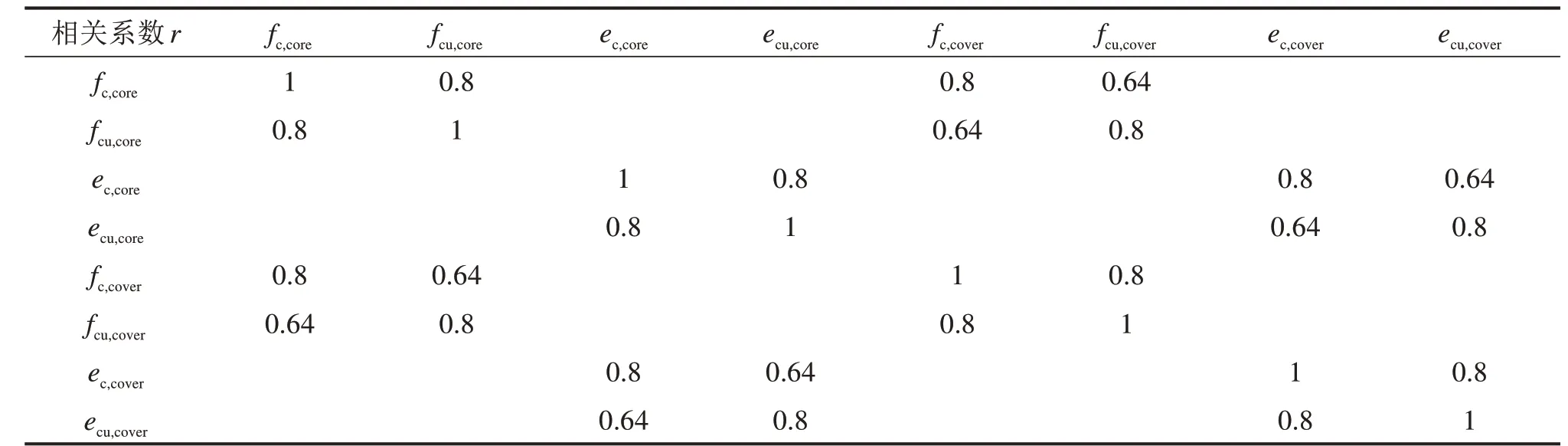
表3 混凝土材料参数相关性系数矩阵Table 3 Correlation coefficient matrix of concrete material

3.2 拉丁超立方抽样

拉丁超立方抽样(LHS)[14]是一种多维分层抽样方法，其抽样效率高、抽样估值稳定，能以较少的抽样次数获得较好的结果，在数理统计及工程实践中运用较广泛。针对矮塔斜拉桥结构参数随机性，具体思路如下：

设桥梁结构随机参数为X，共包含了M个随机变量X1，X2，X3，…，XM，假设每一随机变量Xi(i=1，2，3，…，M)对应已知的分布函数为Φxi(x)，对M个随机变量进行N次抽样，得到N×M维样本矩阵。

将Φxi(x)划分成N个非搭接区间φij(i=1，2，…，M;j=1，2，…，N)，假 设 每 个 区 间 概 率 为Pij，则：

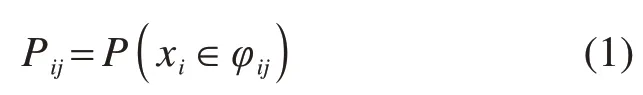
因此，需保证累计概率Pij为1，即：

等概率情况下，Pij=1/N。抽样时，φij(i=1，2，…，M;j=1，2，…，N)按其代表性参数选取，一般可采取2种方法，即随机选取和重心选取。对于随机选取，在(0,1)区间生成N个随机数Ranj(j=1，2，3，…，N)，则由式(3)可将随机数Ranj转化到第j个区间的随机数Rj。

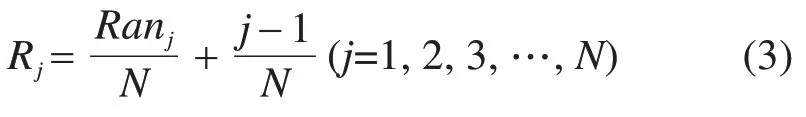
对于Rj满足：

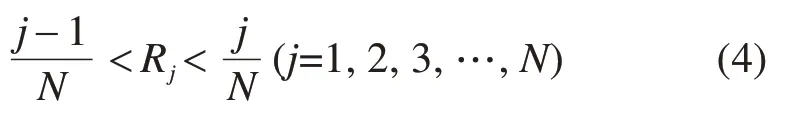
因此，对于生成的随机数Ranj(j=1,2,3,…,N)，可按式(5)求得随机变量在j个区间的随机参数值。

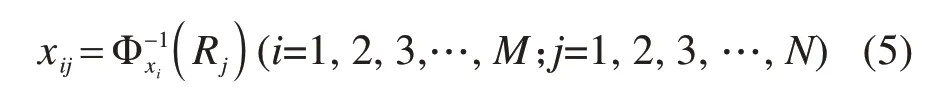
式中：Φxi-1为随机变量x的分布函数Φxi的逆函数。同理，对于区间重心选取情况，xij为：

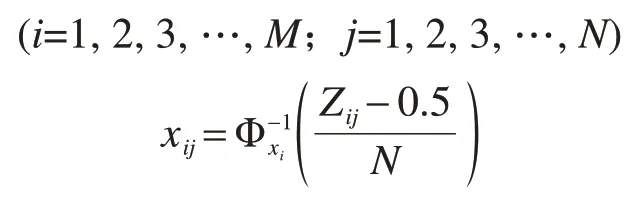
式(6)中的Zij为第i个随机变量的第j个模拟的区间秩数。

对于φij(i=1，2，…，M;j=1，2，…，N)区间在抽样中的选取是随机的，每一个随机变量Xi(i=1,2,3,…,M)的每次抽样对应一个随机整数列(1,2,3,…,N)，对应的M个参数的抽样可形成一个具有N行M列的矩阵Y，如式(7)所示。

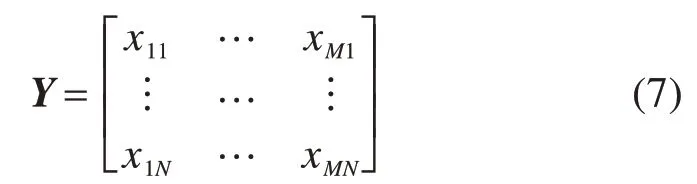
因此，对于第j次抽样，随机变量的区间秩数Zij为矩阵Y的第j行元素。由此可得，矩阵Y为随机变量的抽样策略。

拉丁超立方抽样抽样效率高、抽样估值稳定，能以较少的抽样次数获得较好的结果。从降低抽样结果方差角度出发，对拉丁抽样法方法进行优化，对生成的随机参数Rani，采用逆变换生成服从分布函数的随机参数，如式(8)和式(9)所示。

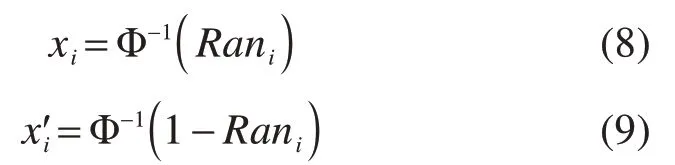
由此可得，优化后的拉丁超立方抽样结果为：

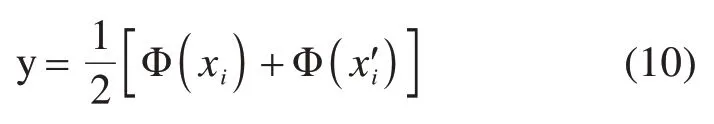
综上，本文针对结构不确定性，采用拉丁超立方抽样对表2所列随机参数生成样本，每个参数对应生成450个样本，用于IDA分析。

4 概率地震需求分析

地震对桥梁损伤本质上体现在结构响应，建立桥梁响应与地震动强度参数二元映射是概率地震需求分析(PSDA)的基础，也是桥梁损伤分析的关键。PSDA主要目标是建立概率地震需求模型(PSDM)。PSDM应当反映不确定性对桥梁动力响应影响。首先，将图3地震波调幅处理，每条地震波从0.1 g～1.5 g按0.1 g增量调幅，共得到450条地震动；然后，考虑混凝土材料相关性，采用拉丁超立方抽样对表2生成450组随机样本；最后，将生成的随机参数样本代入到对应的地震动模型，采用IDA方法，进行非线性动力时程计算分析，再通过云图法[15]将计算的结构响应与地震动强度参数进行回归分析，建立高铁矮塔斜拉桥PSDM。需要说明的是，对于450条地震动与450组样本的组合本文考虑如下：本文讨论了19种不确定性参数，每一种参数生成450个样本。因此一个计算模型，随机对应1条地震波，19种参数随机一一对应其中一个样本，完成一次计算，依此类推完成450次计算。

4.1 概率地震需求模型

矮塔斜拉桥PSDM反映了桥梁响应与地震动强度参数的概率关系，研究假定桥梁地震需求D服从正态分布[16]，需求中位值DM与IM的关系如式(11)所示。

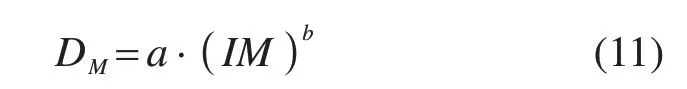
式中：a和b均为未知数，将该式进行对数转换，如式(12)所示。

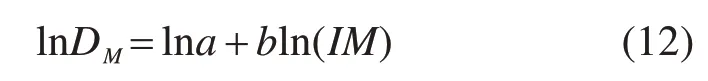
通过对数空间转换，ln D服从对数正态分布，其中位值为ln DM，再根据调幅计算得到的需求峰值Di及地震动强度峰值IMi的数据组(Di，IMi)进行线性回归分析即可得到参数a和b值。因此，矮塔斜拉桥PSDM可表示为：式中：Φ(·)为标准正态分布累积概率分布函数；(ln d−ln a)/b为矮塔斜拉桥地震需求参数对IM中位值自然对数；βD|IM为地震需求对数标准差。

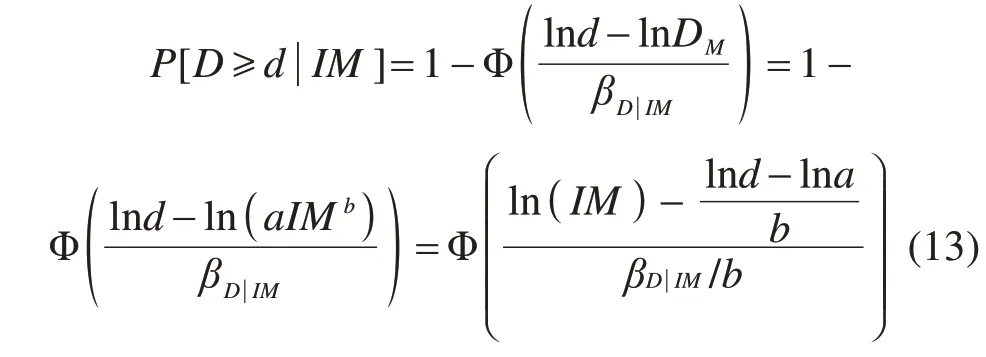
βD|IM的计算关系到易损性曲线的拟合精度，因此本研究标准差按式(14)的4次多项式进行回归计算。

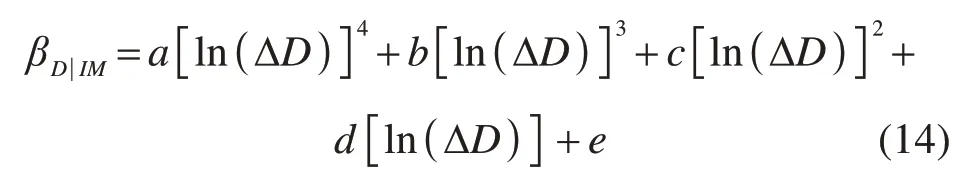
以上推导可得出，对于高速铁路矮塔斜拉桥PSDM本质上是确定桥梁损伤指标地震响应中位值DM及其对数标准差βD|IM，可由IDA分析，再通过云图法将桥梁“响应—地震动强度参数”对数回归分析计算得到。

4.2 不确定性对地震需求影响分析

文献[4]研究了成桥索力变化对该桥内力和线形影响，需严格控制索力。鉴于该研究成果，本文未将索力作为单独影响因素。本文选择墩顶位移、支座位移、墩底曲率、索塔曲率及主梁转角等响应作为地震需求参数，根据上述不确定性参数类别及概率分布特征，地震需求对随机参数的敏感性及受影响程度归纳总结如表4所示。

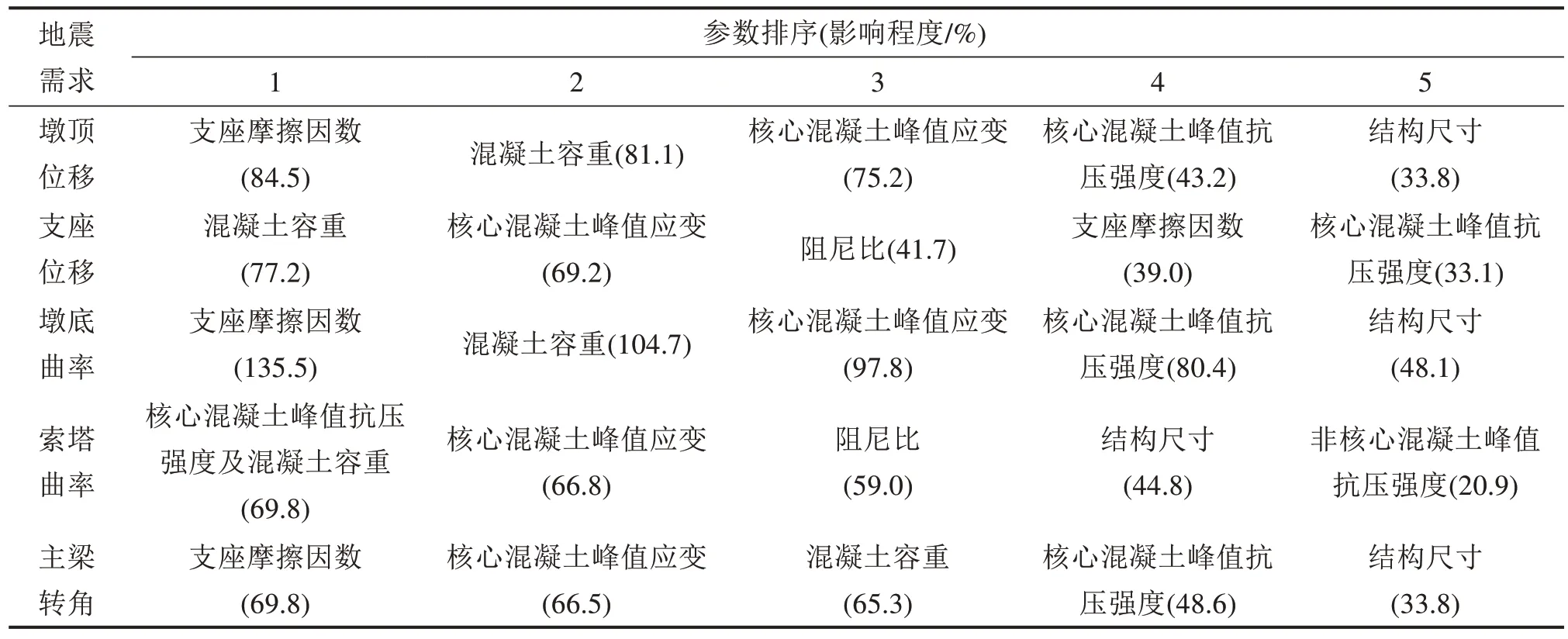
表4 地震需求对随机参数的敏感性及受影响程度Table 4 Sensitivity and influence of seismic demand to random parameters

对比纵、横向地震作用下计算结果可发现，横向地震作用下地震需求受参数变化的影响程度均大于纵向地震作用。限于篇幅，表4所示为横向地震作用下参数敏感性及影响程度。表4影响程度的计算原理为：根据上述抽样方法可得到表2每一随机参数变化幅值，将每一随机参数上限及下限值代入模型，同时其余随机参数保持不变，进行非线性动力时程分析，得到地震需求参数变化幅值(上限与下限值之差)，然后将变化幅值除以基准模型地震需求的最大值，即为随机参数变化对地震需求的影响程度。表4及计算结果可得出支座摩擦因数、混凝土容重、核心混凝土峰值应变、核心混凝土峰值抗压强度、阻尼比以及结构尺寸对高速铁路矮塔斜拉桥纵、横向动力响应影响均较大，占比较高。与此同时，非核心区混凝土的应变和强度对结构响应的影响均不容忽视；对于其他参数影响稍弱。

矮塔斜拉桥PSDM主要工作是建立地震动强度参数与结构响应的关系。同时，βD|IM又受不确定性影响。因此，针对矮塔斜拉桥力学特性，本研究选取PGA作为地震动强度参数，考虑纵、横向地震作用下，分别构建PGA对应的PSDM，讨论不确定性对PSDA影响。以11号墩为例，PGA对应的墩顶及支座位移、梁端转角、墩底和索塔底曲率等回归系数如表5所示，顺桥向地震作用下，其标准差回归分析如图4所示；横桥向地震作用下，标准差回归分析如图5所示。

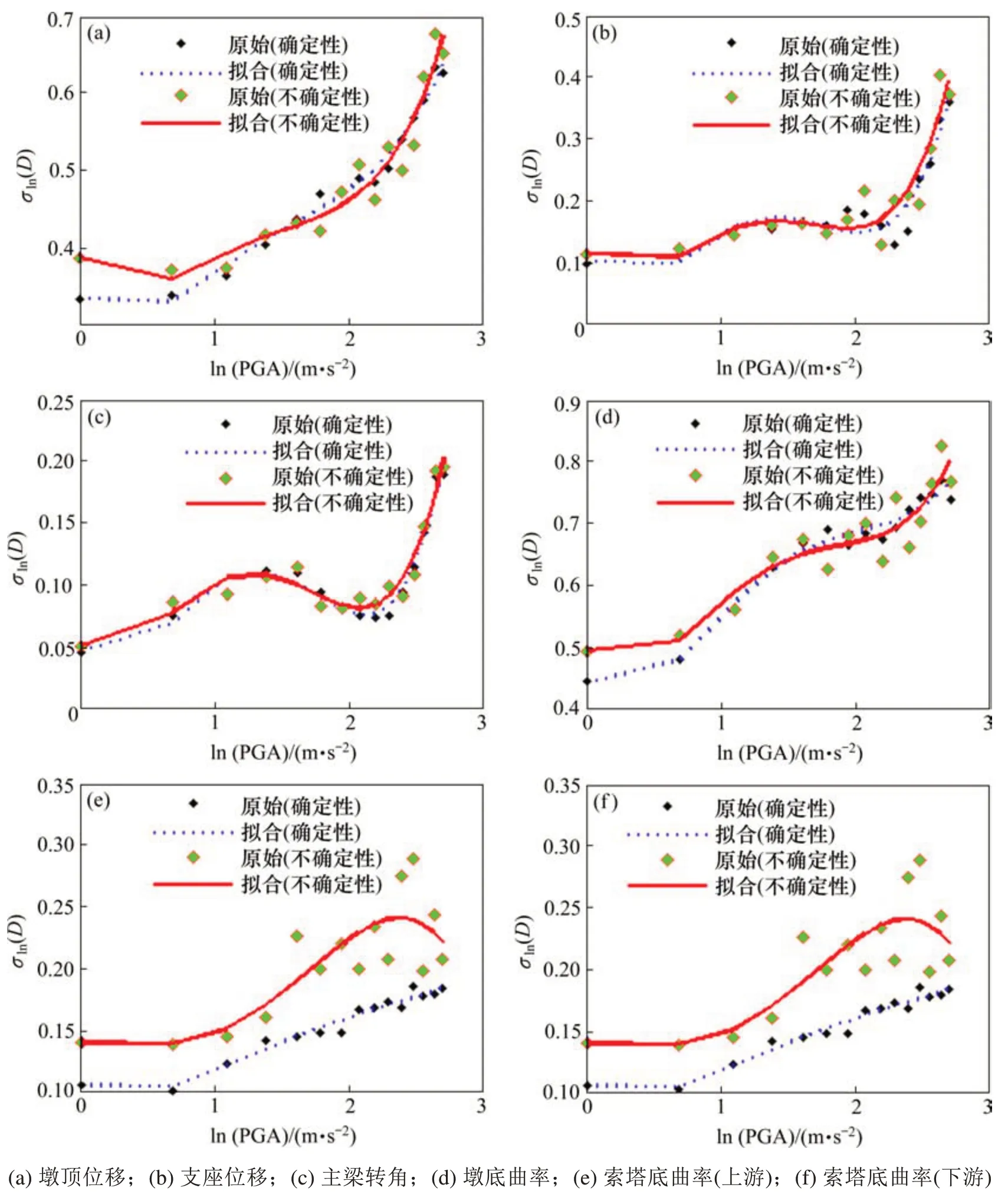
图4 地震需求参数标准差拟合分析(顺桥向地震作用)Fig.4 Fitting analysis of standard deviation of seismic demand parameters(seismic response in longitudinal direction)

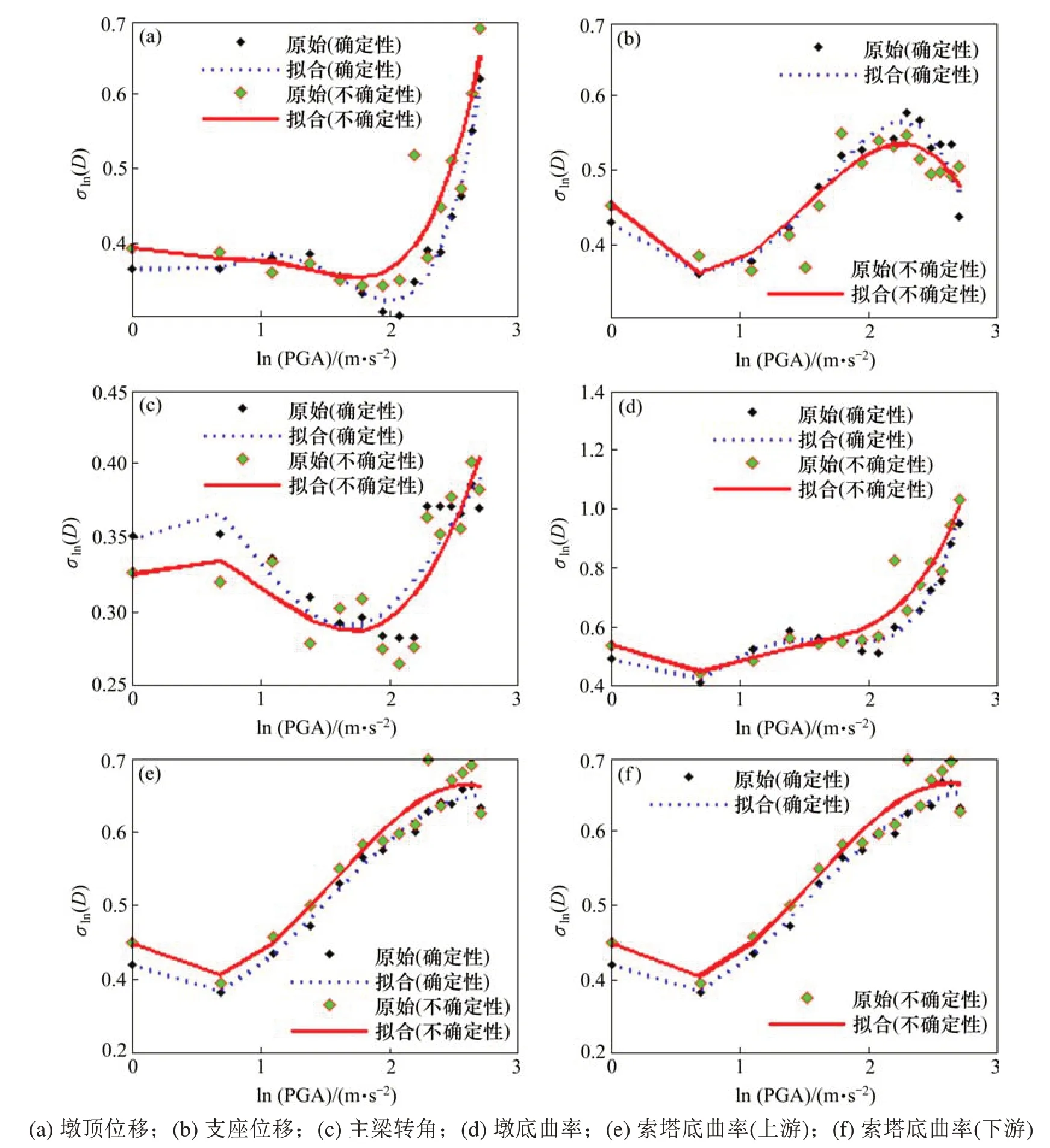
图5 地震需求参数标准差拟合分析(横桥向地震作用)Fig.5 Fitting analysis of standard deviation of seismic demand parameters(seismic response in transverse direction)

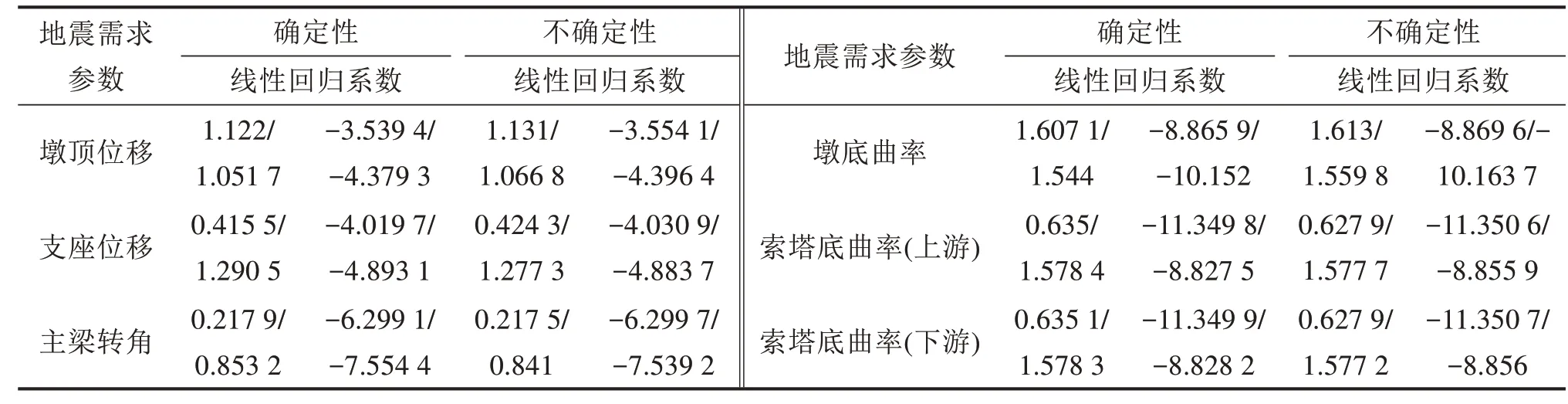
表5 地震需求参数线性回归分析对比(顺桥向地震作用/横桥向地震作用)Table 5 Linear regression analysis and comparison of seismic demand parameters(seismic response in longitudinal direction/seismic response in transverse direction)

通过上述对比分析可得知，地震需求参数线性回归分析以及结构响应标准差受结构不确定性影响显著。纵向地震作用下，考虑不确定性与确定性，墩顶位移、支座位移、主梁转角和墩底曲率标准差拟合趋势虽大致相同，但其数值差异明显；对索塔曲率的影响较大，不仅变化趋势存在差异，其标准差变化也较大。横向地震作用下，各地震需求参数标准差拟合趋势大致相同，但其数值差异明显。纵横向地震作用下，除了横向地震下的主梁转角，其余地震需求参数变化趋势相同，考虑不确定性的标准差要大于确定性的。因此，进行桥梁易损性分析时，若忽略结构不确定性，构件损伤概率的准确性将受到较大影响。此外，纵横向地震作用下索塔、主梁转角标准差拟合变化也可得出，由于结构体系的差异性，对于高速铁路矮塔斜桥易损性分析，需进一步研究地震对索塔损伤的影响；将主梁转角作为地震需求参数，可进一步探索铁路与公路桥梁损伤对后期运营功能的影响，这2个方面也是后期可开展的研究。

5 结论

1)支座摩擦因数、混凝土容重、核心混凝土峰值应变、核心混凝土峰值抗压强度、阻尼比、结构尺寸、非核心区混凝土的应变和强度是影响高速铁路矮塔斜拉桥地震需求的敏感参数。因此，精确计算材料及结构动力特性，准确模拟纤维截面，确保构件设计尺寸准确是保障计算结果准确可靠的前提。

2)概率地震需求作为易损性分析的基础，结构不确定性对高速铁路矮塔斜桥概率地震需求参数回归分析及需求参数标准差的影响显著，忽略不确定性及不合理的不确定性分析最终将影响桥梁损伤超越概率。

3)结构不确定性对高速铁路矮塔斜拉桥概率地震需求分析影响表明，索塔及主梁转角不同于其他地震需求参数。因此，不同于常规梁式桥梁地震需求参数，探明主梁转角和索塔与随机参数的关系，对进一步厘清桥梁地震损伤，探索铁路桥梁损伤对后期运营功能的影响，具有理论及实践意义，也是保障桥梁地震易损性分析准确可靠的基本前提。