基于生成对抗网络的地铁OD需求短时预测
申慧涛,郑亮,李树凯,王璞
(1.中南大学 交通运输工程学院,湖南 长沙 410075;2.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044)
城市轨道交通是城市公共交通系统的重要组成部分,可以很大程度地解决城市交通拥堵、汽车尾气排放等问题,实现城市绿色健康发展。然而客流规模的增长、线网复杂度的增大以及线路运营里程的增加也给城轨系统的运营管理带来了挑战,如列车供给与乘客需求不匹配、高峰期拥堵、大客流疏散等[1]。地铁客流需求与地铁服务水平、运输能力之间的矛盾日益突出。因此,实现可靠、准确的地铁短期客流预测对旅客出行与地铁管控具有重要意义。以往关于地铁客流预测的研究主要集中在地铁进出站客流的预测[2−6],很少关注乘客出行的OD需求。然而,进出站客流的预测只能得到某个站点进出站的客流量大小,并不能体现乘客需求的具体分布,即站点与站点之间的具体客流量大小,因此,短时OD需求预测能更好地为地铁动态化运营和管控提供指导依据。一般来说,地铁OD矩阵具有数据量大、高维度和高度稀疏等特点[7]。具体来说,由于线网复杂度的提升,地铁站点数量剧烈增加,故而OD对的数量急剧上涨,但不同OD对的客流量差距悬殊,如部分距离远的OD对需求极低,造成地铁OD矩阵高度稀疏的特征。除此以外,在目前大客流的环境下,高峰期间地铁客流的出行量极大,因而一天之中OD需求的波动也会变大,OD对之间存在复杂的和隐性的时空关联性。因此,相比于进出站客流预测,基于OD矩阵的客流预测显然是一项更具挑战性的任务。目前,地铁OD需求预测的文献主要集中在传统数学模型、传统机器学习方法以及深度学习方法3个方面。姚向明等[8]根据乘客行程时间建立数学模型预测地铁OD,但面对高度复杂的现代地铁系统,预测精度有限;DAI等[9]提出了一种组合预测框架,通过概率拟合模型将k邻近和自适应增强2种传统机器学习方法组合,并用于预测地铁OD需求;车国鹏等[10]则提出了遗传算法优化的BP神经网络,避免了传统BP网络训练速度慢、易陷入局部极值等缺陷。上述研究使用传统机器学习方法,相对于传统数学模型在预测精度上得到了一定的提升,但面对当今地铁需求数据量大、时变性高的场景,仍不尽人意。近年来,随着大数据与人工智能技术的飞速发展,深度学习在语音识别、图像处理等许多任务中取得了很好的效果,给学者带来了新的预测方法。TOQUÉ等[11]将矩阵向量化为长短时记忆网络的数据结构,并预测了地铁网络中的OD矩阵。结果表明,深度学习能很好地捕捉地铁OD数据中的非线性特征,相比于传统机器学习算法和传统数学模型,深度学习方法能极大地提高预测精度。然而,长短时记忆网络隶属于递归神经网络,虽然解决时间序列问题时优势巨大,但无法很好地挖掘OD矩阵中数据之间的空间相关性。生成对抗网络作为深度学习的前沿技术,具有强大的生成能力,在不少领域展现出了比传统深度学习更好的性能[12]。当下,已有部分学者使用生成对抗网络进行交通预测。ZHANG等[13]首次尝试使用生成对抗网络估计旅行时间分布,并提出一个出行信息最大化生成对抗网络(T-InfoGAN)模型,在考虑路网时空相关性的情况下,通过对2条连续链路的出行时间联合分布进行建模,成功地估计了旅行时间;ZHANG等[14]通过对数据完整的链路的旅行时间建模,提出了一种旅行时间补全生成对抗网络(TTI-GAN),可以在数据缺失的链路上生成旅行时间。以上应用证明,生成对抗网络能很好应对数据量大、维度高的复杂任务,符合地铁OD需求的特点,而且结构灵活,可以结合其他深度学习的框架,挖掘OD对之间隐含的时空联系,并引入辅助信息,引导更加精准的预测结果。但在国内几乎没有学者使用该技术预测地铁OD需求,本文首次使用生成对抗网络预测短时地铁OD需求,不仅具有理论意义,也具有指导地铁运营和客流管控的现实意义。
1 基于生成对抗网络的短时预测模型
1.1 生成对抗网络
作为一种前沿的深度学习方法,生成对抗网络主要由2部分组成的:生成器G和判别器D。生成器G用于学习并捕捉真实数据的分布,目标是生成“以假乱真”的数据分布,以达到“欺骗”判别器D的目的;而判别器D则用于区分真实数据和生成器G生成的数据,目标是尽可能准确地判断该输入是采样自真实数据还是由生成器G生成的。
图1(a)展示了原始生成对抗网络的基本结构,其中,z表示模型输入的数据。生成对抗网络发明者GOODFELLOW等[15]表示,生成器G与判别器D的训练过程体现了博弈论中“零和博弈”的思想——即生成器G与判别器D的训练过程实质上就是这两者对抗和进化的过程。在训练过程中,生成器G生成数据的能力不断增强,所生成的数据越来越接近真实分布;而判别器D的判别能力也会随之增强,区别数据真假的本领也逐渐提高。整个训练过程的目标函数可以归纳为公式(1),其中Pdata(x)表示真实数据x的分布,Pz(x)表示输入数据z的分布:
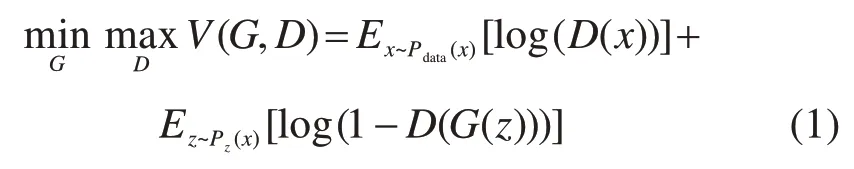
虽然原始生成对抗网络在一些领域取得了瞩目的成就,但仍存在生成效果难以控制、训练不稳定、不收敛等问题。后续关于生成对抗网络的研究主要集中于解决以上问题。一方面,部分学者着力于提高传统生成对抗网络生成数据的质量,并认为原始生成对抗网络预测性能较差与它自由度太广有关。为了提高训练结果的精确性,MIRZA等[16]认为可以根据实际需要在训练过程中引入“条件信息(conditional information)”,以达到“引导”生成器生成数据的目的。在传统的生成对抗网络输入额外的条件信息c后,即扩展成了CGAN模型,具体结构如图1(b)所示。额外的条件信息c可以是任意有助于生成目标的辅助信息,如特征标签、时间标签等。
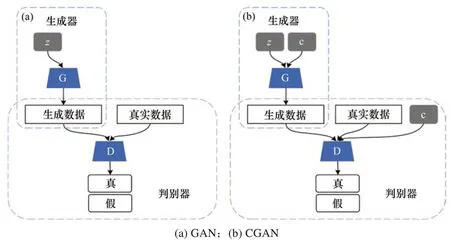
图1 原始GAN和CGAN的基本结构Fig.1 General structures of the original GANs and CGANs
另一方面,也有部分学者着力于提升生成对抗网络的稳定性。原始的生成对抗网络使用Jensen-Shannon散度衡量生成器所生成数据与真实数据之间的差别,而不少学者证明可以使用Wasserstein距离替代它。于是,原始的生成对抗网络便衍生出了一系列的WGAN模型[17−19]。其中,WU等[19]提出的WGAN-div模型在一众WGAN模型中具有较好的稳定性。不同于其他学者提出的WGAN模型,WGAN-div不仅解决了原始GAN训练不稳定和收敛速度慢等问题,而且它的提出具有严格的理论基础。WGAN-div的目标函数V(G,D)如公式(2)所示,其中k和p是参数,Pu则是关于真实分布Pr和生成分布Pg的函数。通常可以设定Pu为Pr和Pg的加权平均,如公式(3)所示,其中ε为参数,͂~Pu,xr~Pr,以及xg~Pg。

综上所述,为了保证数据预测质量的同时保证模型的稳定性,本文提出一个融合了CGAN和WGAN-div关键结构的模型,即CWGAN-div模型。下面介绍CWGAN-div的技术细节。
1.2 基于CWGAN-div的客流预测模型
一般认为,地铁客流需求在时间上存在2种相关性。一方面,客流需求具有短期的自相关性,即客流会受过去一段时间内客流量的影响;另一方面,客流需求具有长期的自相关性(周期性),即类似日期(如工作日、休息日)相同时间段(如早高峰、晚高峰)的客流量呈现出相似特征。为了提高预测的准确性,本文同时考虑这2种地铁客流需求的相关性。一方面,为了考虑短期的自相关性,模型的输入z被设定为一段时间的历史OD需求;另一方面,为了考虑长期的自相关性,本文引入ZHANG等[13]提出的Timestamp*day时间标签用作模型输入的条件信息c。这种时间标签使用独热编码的方式,其中Timestamp是时间段的标签,Day则是星期的标签。根据CGAN和WGAN-div的原理,可以推出CWGAN-div的目标函数如公式(4)所示;进一步可以推出生成器G与判别器D的损失函数分别如式(5)和式(6)所示。基于CWGAN-div客流预测模型的具体框架如图2所示。

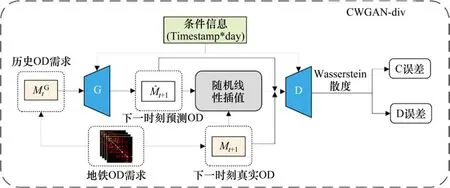
图2 基于CWGAN-div的OD预测模型结构Fig.2 Internal structure of CWGAN-div based OD prediction model
1.3 CWGAN-div模型中G和D的结构
原始的GAN模型仅要求生成器G和判别器D具有拟合和判别功能,并不指定G和D的函数形式。受深度学习在各领域出色应用的启发,后来的学者主要使用人工神经网络构建G和D。因此,本文采用改进的卷积神经网络结构,即残差神经网络模型构建生成器G和判别器D。
得益于其特殊结构,卷积神经网络在处理图像类数据时不仅可以避免人工神经网络节点过多的困扰,还可以在时间和空间2个维度挖掘数据间的非线性关系。但在加深网络结构的同时,卷积神经网络可能面临梯度弥散和网络退化等问题,残差神经网络在卷积神经网络的结构上增添了快捷连接的结构,很好地解决了这一问题。为了加快GAN模型的收敛,防止退化现象,在生成器G与判别器D的结构中引入残差神经网络。综上所述,生成器G和判别器D的具体网络结构如图3所示。
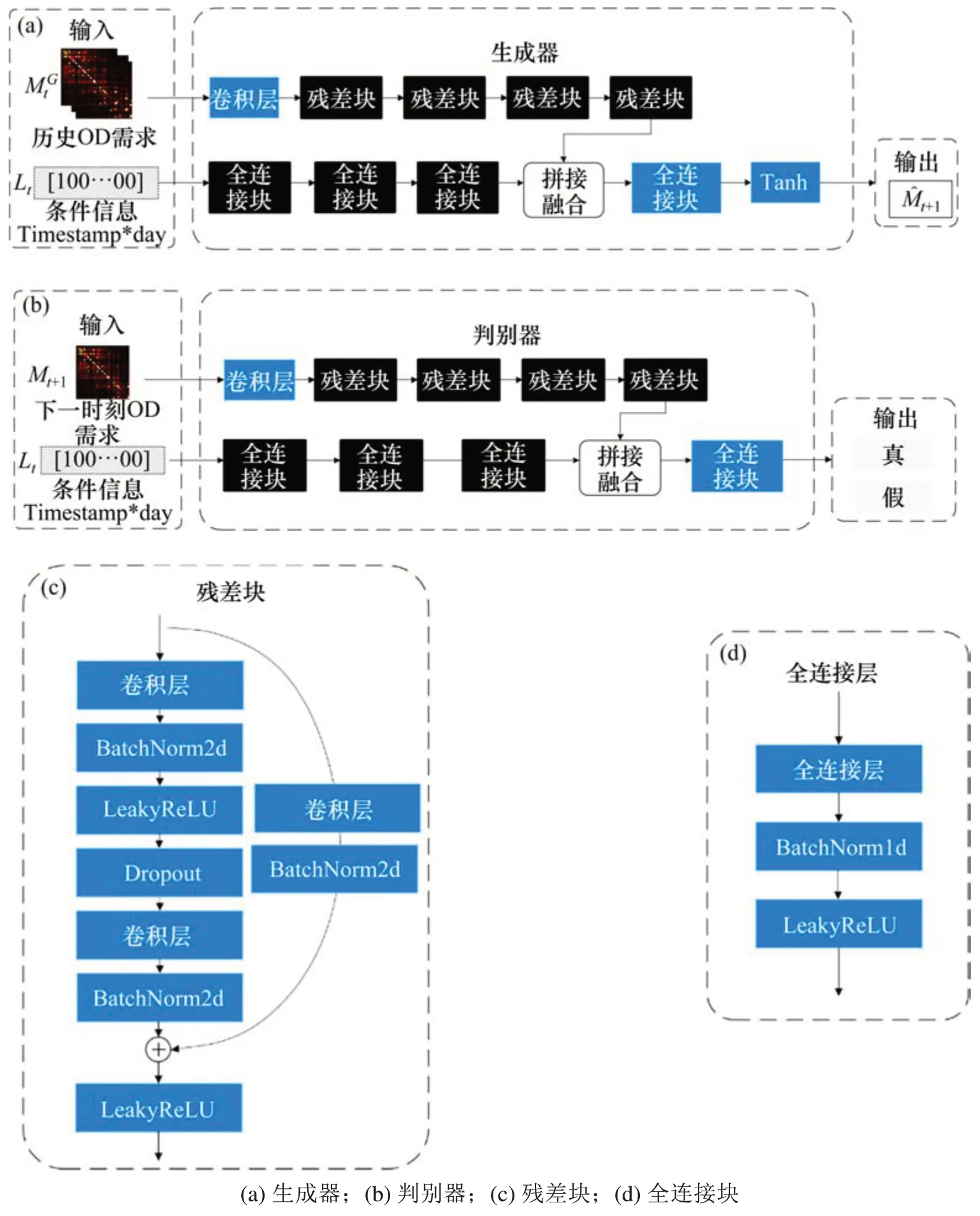
图3 生成器G与判别器D的网络结构Fig.3 Structures of the generator G and the discriminator D
1.4 CWGAN-div模型的训练过程
CWGAN-div模型训练过程如下所示,其中各符号的意义与图3中出现的符号意义相同。
1)从数据库中取历史OD矩阵样本MG t与对应的下一时刻OD矩阵数据Mt+1,并记录相应的Timestamp*day为Lt;
2)将MG t和Lt输入生成器,并获得预测值,然后根据公式(3)计算得到插值结果
4)根据式(5)~(6)计算生成器G与判别器D的损失函数;
5)计算生成器G与判别器D的损失梯度,并使用Adam优化器训练生成器G与判别器D;
6)训练完成后保存最优模型,并使用最优模型预测OD需求。
2 实验与结果分析
2.1 数据来源与数据处理
本文选取深圳市地铁1号线与4号线的44个站点作为数值实验的对象,如图4所示,44个站点之间存在1 936个OD对。数据来源于出入站刷卡数据,采集间隔为30 min,因此本文短时预测的时间间隔为30 min。数据范围为2014年10月9日~2014年11月18日的40 d,并设定其中的前36 d为训练集,最后4 d为测试集。数据处理的过程如下:1)研究范围数据筛选:首先筛选出实验场景1号线、4号线的各个站点的数据。2)原始数据有效性检验:剔除数据集中的异常数据,包括进出站时间在运营时间之外(可能由站点工作人员晨间夜间工作进出站造成)、进出站相同(可能由工作人员进出站、乘客错误进站造成)的数据。3)OD信息及辅助信息的提取和处理:将线网中观测到的44*44个OD客流处理成维度为44*44的OD矩阵,并记录下每个时刻对应的Timestamp*day时间信息。最后,为了提高模型的稳定性和训练速度,采用min-max方法将OD数据标准化到[−1,1]区间。

图4 深圳地铁1号线和4号线Fig.4 Shenzhen Metro Line 1 and Line 4
图5展示了40 d内的OD需求具体分布,图5(a)表现的是1 936个OD对的平均需求变化趋势,可以看出,OD需求波动强烈,并具有明显的时间周期性,即在一天之内和一周之内的变化趋势相似。OD需求预测除了的预测目标数量多,不同OD对的需求规律具有较大的差别也带来挑战性。图5(b)展现了“深圳北站−会展中心”和“罗湖−会展中心”2个OD对40 d内的变化趋势,两者不仅在一天之内的变化趋势并不相同,而且同一时刻的需求差值巨大。
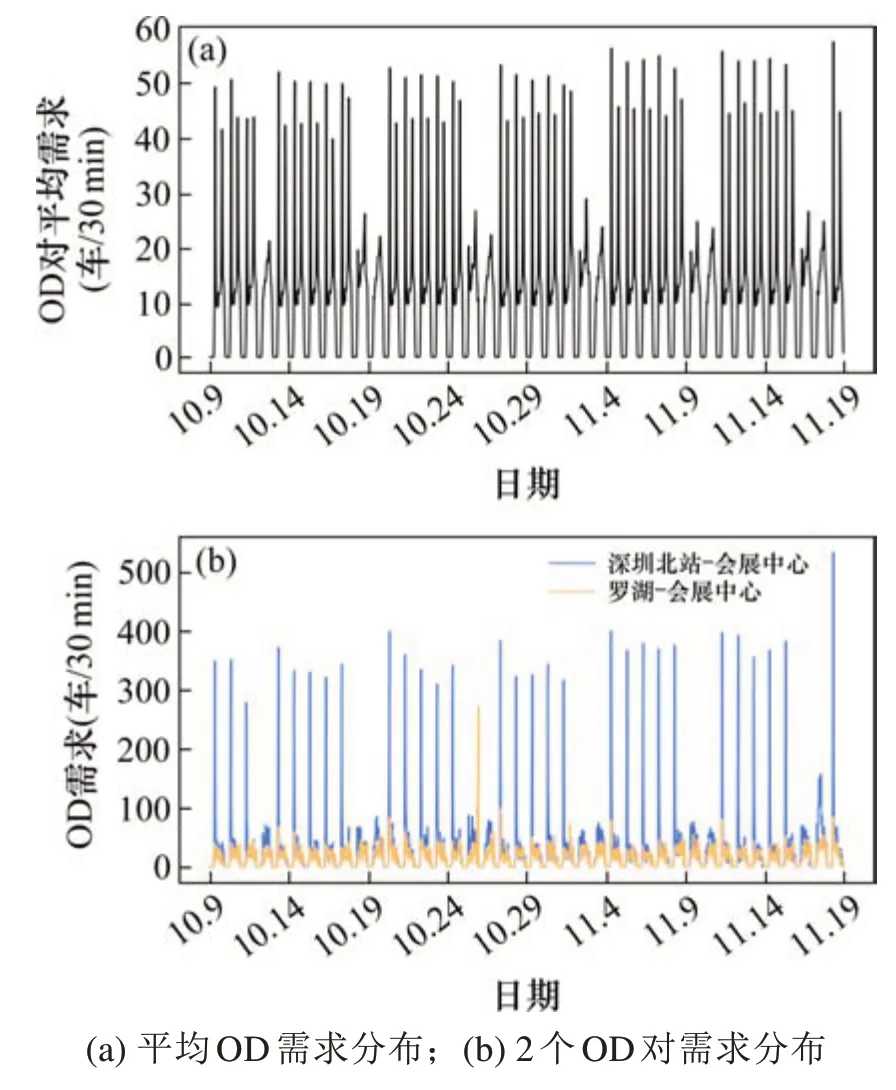
图5 数据集OD需求具体分布Fig.5 OD Demand Distribution
2.2 对比模型与评价指标
为了验证模型的有效性,本文选取2种常用的传统预测算法与CWGAN-div对比,分别是历史平均(HA)和卷积神经网络(CNN),后者作为一种深度学习方法已在交通需求预测,特别是OD需求预测领域被学者们多次使用。为了对比CWGAN-div模型与其他组合式算法的性能,鉴于OD需求具有时间与空间双重的关联性,长短期记忆神经网络(LSTM)与CNN的组合算法能分别挖掘2方面的内在联系,近年来有学者采用两者的组合算法进行交通预测[20−21],因此选取CNN与LSTM的组合算法(CNN-LSTM)进行对比,将需求分别输入LSTM网络和CNN网络中,再联合输出最终的预测结果。除此以外,为了验证CWGAN-div模型与基础GAN模型性能的差异,选取CGAN模型和WGAN-div模型进行对比。这5种对比测试算法的结构参数如下所示:
1)HA:将过去4个时间段的历史需求进行平均,作为下一时刻乘客需求预测;
2)CNN:包含4个卷积层(通道数分别为32,128,256,512),4个最大池化层和1个全连接层;
3)CNN-LSTM:CNN部分为4个卷积层(通道数分别为32,128,256,512)和4个最大池化层,LSTM部分为3层神经元数量为1 024的LSTM层,最后使用一个全连接层将2部分结果融合输出;
4)CGAN:生成器G与判别器D结构与CWGAN-div模型大致相同,但目标函数采用原始GAN的JS散度来衡量;
5)WGAN-div:生成器G,判别器D结构与CWGAN-div处理OD矩阵部分相同,目标函数也与CWGAN-div相同,但没有时间信息作为条件信息输入。
本文使用平均绝对误差(MAE)和平均百分比误差(MAPE)作为预测准确度评价指标,计算方法如下:
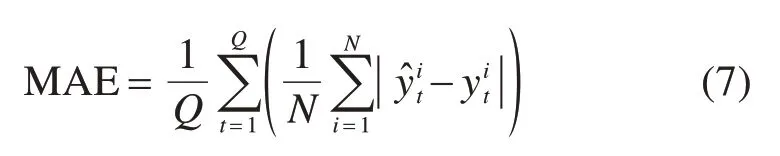
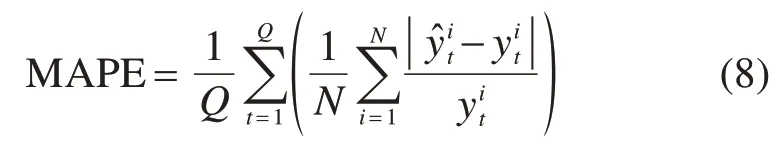
其中:Q表示预测的时段数量;N表示OD对的数量;̂it表示t时段OD对i的预测结果;yit则表示t时段OD对i真实需求。
所有的数值实验都在一台配备16 GB内存的Core i5-10200H中央处理器和GeForce RTX 2060图形处理器的台式计算机上进行。经过反复调参,最终生成器中处理OD矩阵网络结构为:卷积层通道数为32,4个残差块的通道数分别为32,32;32,64;64,128;128,256;256,512。生成器中处理时间信息的网络结构为:全连接层的节点数依次为128,64,32。判别器网络结构中处理OD矩阵与时间信息的通道数与节点数和生成器相同。实验的训练步数为3 000步,并使用Adam优化器优化模型中的参数。
表1展示了CWGAN-div模型与以上对比模型在测试数据集上预测效果。可以看出,本文提出的CWGAN-div模型表现最佳,对高度变化且复杂庞大的预测目标,CWGAN-div模型的预测性能相比传统的历史平均方法及常用的深度学习方法CNN更胜一筹,精度分别提高了31.06%和5.95%。此外,CNN-LSTM算法考虑到时空信息,比传统算法精度略有提高,但相比CWGAN-div预测误差仍增大了3.26%。同时,CWGAN-div模型预测性能也优于基础WGAN-div和CGAN模型,精度分别提高了9.51%和3.83%,可以发现时间信息对预测效果的提升十分显著。图6以深圳北站-会展中心OD对为例,具体展示了6种模型与真实需求的拟合情况,拟合度与以上结论相符合。
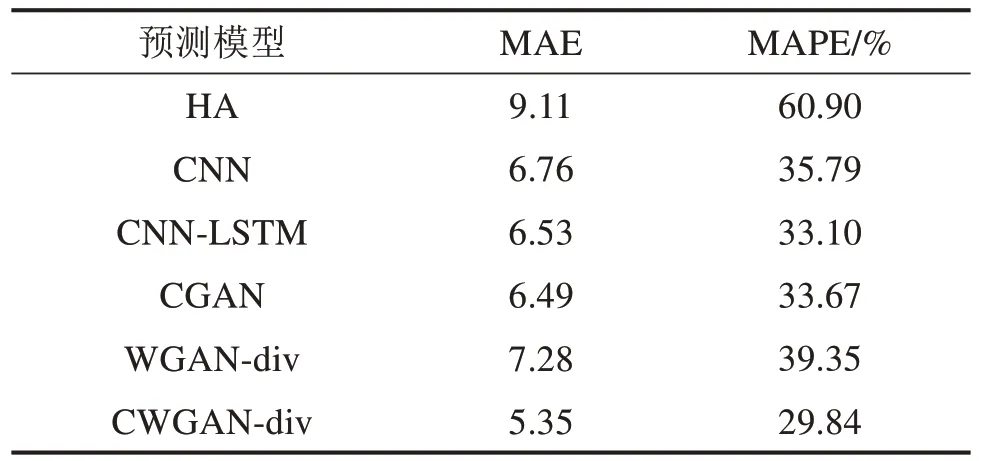
表1 各模型预测结果对比Table 1 Comparison of prediction results with five models
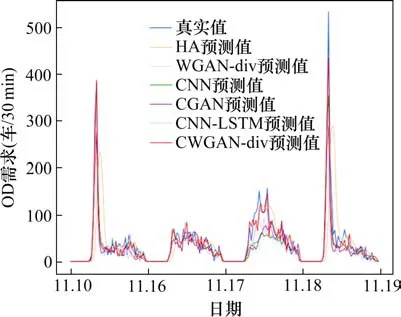
图6 不同预测方法在OD对(深圳北站−会展中心)预测结果对比Fig.6 Comparison results of OD pair(Shenzhenbei-Huizhanzhongxin)and real data
2.3 实验结果及分析
为直观表现预测结果,本文用热力图展示11月16日早高峰8:30~9:00和晚高峰18:00~18:30 2个时段的OD矩阵及预测结果,如图7所示。热力图的横轴代表到达车站,纵轴代表出发车站,像素块的颜色越明亮,表示2个车站之间的客流需求越大。可以看出,早晚高峰真实OD与预测结果都较为吻合。

图7 预测结果与真实数据对比Fig.7 Comparison of predicted results and real data
图8(a)和8(b)分别展示了训练过程中生成器G和判别器D的损失函数变化趋势。为了验证残差神经网络的效果,进一步将本文模型与未使用残差网络结构的模型生成器与判别器的损失函数进行对比。使用残差网络结构的模型,起初生成器与判别器的损失函数都剧烈震荡,在150步左右,生成器与判别器都迅速收敛,最终收敛至0附近。未使用残差神经网络得模型,生成器难以收敛,判别器收敛速度较慢,在1 500步后初见收敛迹象。以上结果表明残差神经网络的使用可以提高生成对抗网络的稳定性,并加快模型的收敛速度。

图8 训练过程中生成器与判别器的损失函数Fig.8 Loss function of the generator and the discriminator in training procedure
图9展示了训练过程中训练数据集与测试数据集的平均绝对误差变化情况(训练过程中预测数据尚未反标准化),通过比较两者随着训练步数增加的趋势走向,可以看出测试数据集并没有随着训练数据集误差的下降而出现误差回弹,证明无过拟合现象。

图9 训练过程中训练数据集与测试数据集的误差变化Fig.9 Loss of training dataset and test dataset in training procedure
3 结论
1)本文提出的CWGAN-div模型结合了CGAN与WGAN-div的优点,可以稳定、准确地预测具有数据量大、变化快、数据稀疏等特征的地铁OD需求矩阵,为地铁运营动态管理提供决策依据。
2)相比传统的预测方法(HA)、普通的深度学习方法(CNN)、基础生成对抗网络模型(CGAN和WGAN-div),CWGAN-div模型的预测效果最好。
3)残差神经网络结构能极大提高生成对抗网络模型的稳定性,加快模型的收敛速度,提高了CWGAN-div的适用性。
4)地铁OD矩阵数据量大、高度稀疏性的特点可能会对模型训练造成负面影响,后续可以考虑先将OD矩阵压缩降维再预测。

