基于系统动力学的城市轨道交通车站客流控制仿真与优化

陈慧，汪波，朱江斌

(1.闽江学院 经济与管理学院，福建 福州 350108；2.北京市交通信息中心，北京 100044；3.福州地铁集团有限公司，福建 福州 350009)*

随着城市轨道交通线网的不断扩增，客流规模逐年攀升，车站大客流逐渐成为常态.目前我国大部分车站在实际运营中客流控制方案制定仍然依靠人工经验[1]，迫切需要从系统化、定量化、易操作、直观角度对客流控制策略优化进行研究，为车站运营管理提供决策支持.

目前，国内外学者对城市轨道交通客流控制的研究主要集中在以下方面：周云娣[1]对南京地铁进入网络化运营后的车站级、线路级和线网级三个层次的客流控制措施进行了研究.部分学者分别以客流聚集预警值最小和乘客等待时间最小为目标[2]，以人均延误最小和各区间运力满载率之和最大为目标[3]建立多目标规划模型来构建线网客流控制模型.陈波等[4]以车站三级客流控制为依据，对大客流组织原则、影响因素和应对措施进行探讨.蔡琦玮等[5]以空间分区间控制节点的通过能力与客流需求相匹配和资源节约为目标建立多目标整数规划模型.郑雪梅等[6]通过构建车站系统动力学模型对车站客流进行仿真，并通过仿真实验对不同的限流方案效果进行验证.薛霏等[7]提出了轨道交通换乘站客流流动模型，并对车站客流的动态演变算法及其实现进行研究.Xu Xinyue[8]等对不确定需求下的车站客流组织研究，就不同客流场景提出3种模型，并提出基于仿真的求解算法.总结以上学者，既有的基于系统动力学方法的车站客流控制研究大多仅呈现不同客流控制方案效果，缺乏对控制策略的优化研究.因此，本文根据现行广泛应用的车站三级客流控制理论及实践经验，提出了基于系统动力学的车站客流控制模型，并对车站客流控制策略优化进行研究.

1 客流控制模型构建

1.1 系统要素

城市轨道交通车站建模主要包括车站设施、客流及运营组织三要素[6].本文引入客流控制系数Ri来构建车站客流控制模型.通过对系统各要素间相互作用及因果关系分析，建立基于系统动力学的车站客流控制模型混合图[9]，如图1所示，模型中定义的相关变量如表1所示.

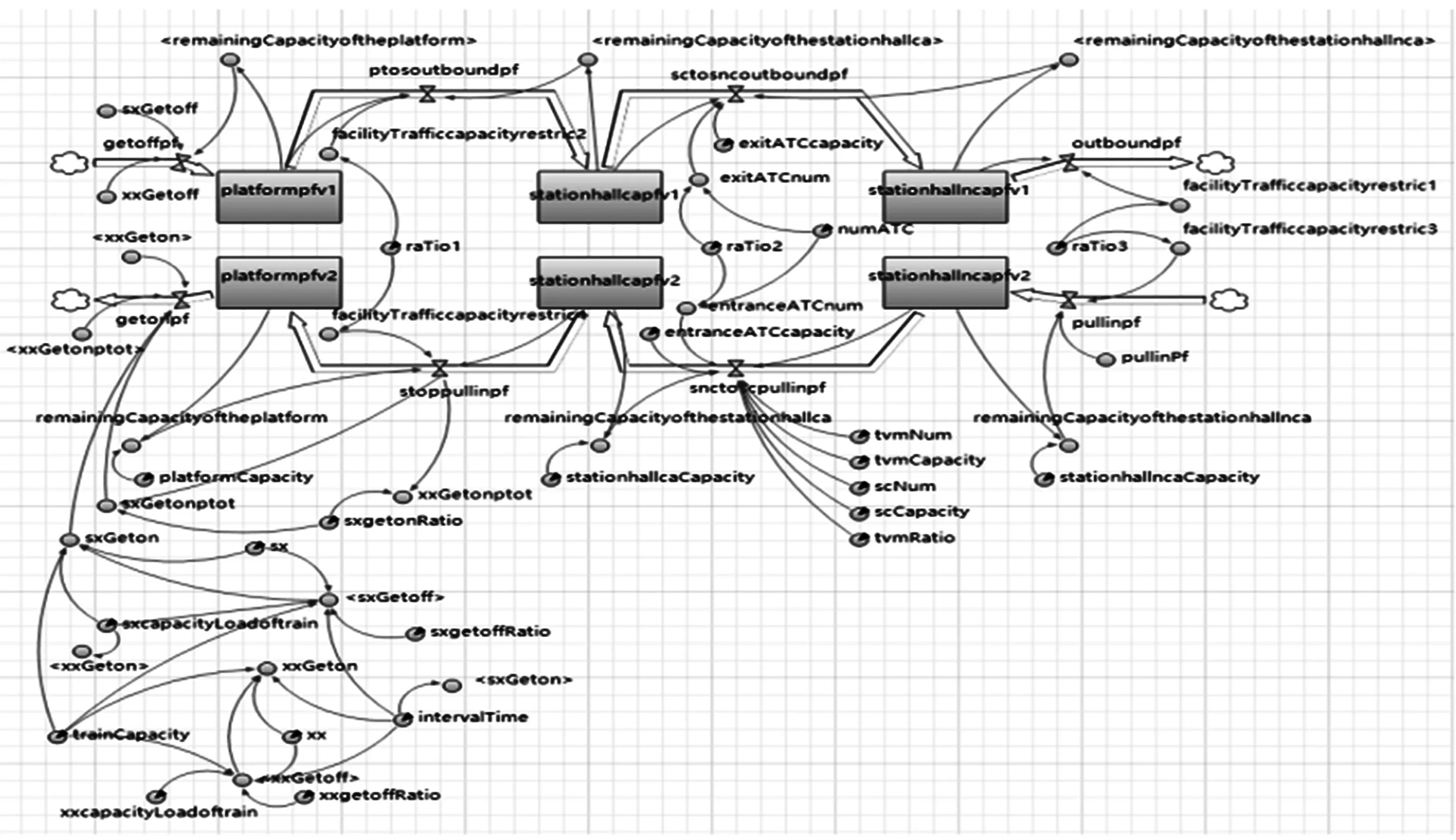
图1 车站客流控制模型混合图

表1 变量说明表

1.2 系统动力学方程构建

依据车站客流在各设备间的动态演化规律及车站客流控制措施，建立系统动力学方程如下：

(1)状态变量计算方程

(1)

式中：Qi为车站客流承载区域i在t时刻的客流量.Fiin(t)为t时刻客流流入客流承载区域i的速率；Fiout(t)为t时刻客流流出客流承载区域i的速率.

(2)速率变量计算方程

①连接设备处客流流动方程

i=3,1;j=1,4

(2)

② 衔接节点处客流流动方

(3)

(4)

③进出站客流流动方程

(5)

F6in=min{RQ6,RF6in,Fin}

(6)

④上下车客流流动方程

F1in=min{FS1in+FX1in,RQ1}

(7)

(8)

(3)辅助变量计算方程

①设施剩余承载力

RQi=RQi+1=CQi(i+1)-Qi-Qi+1,

i=1,3,5

(9)

②客流控制系数Ri

车站客流控制措施是影响车站客流分布的关键因素之一，当某监测区域客流承载量超过预警值时，运营管理者通常会在与其关联设施上采取疏导或限流措施来控制客流流动，如改变电扶梯运行方向、在双向通行通道设置隔离栏对进出站客流进行分离等.本模型引入客流控制系数Ri来表示车站客流控制措施.

(10)

(11)

(12)

2 客流控制策略优化

2.1 车站大客流类型

由于通勤、旅游以及节假日等因素影响[10]，车站客流将呈现波动，因此，根据车站客流控制措施特点，分为以下两种类型进行讨论：

(1)客流类型一：下车出站客流持续较大或下车出站客流与进站乘车客流同时持续较大的情况.

(2)客流类型二：进站乘车客流持续较大且下车出站客流较小的情况.

2.2 车站大客流控制策略优化

2.2.1 车站大客流控制基本思路

目前，我国大部分车站客流控制秉持“加快出站速度、限制进站客流”等基本原则[4]，应对大客流时常采用自内而外的三级客流控制原则, 当站台候车乘客达到拥挤时控制站台站厅间的楼梯和扶梯；当付费区乘客达到拥挤时控制闸机的开启数量，延缓乘客进入付费区的速率；当非付费区达到拥挤时控制出入口处设备，减缓进站客流速率[5].

2.2.2 车站客流控制系数优化

本文引入客流控制系数Ri及站外限流数值Φ建立车站客流控制模型，从系统角度出发，研究车站各设施客流控制协调性，分类型客控措施优化步骤如表2、表3所示；分类型大客流的客控系数Ri及Φ优化流程如图2、图3所示.

表3 车站大客流客控措施优化步骤(客流类型二)

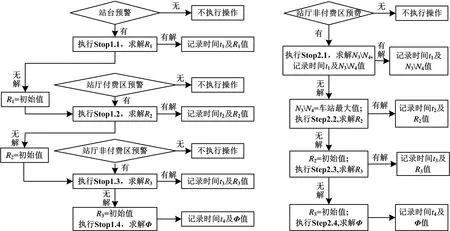
图2 大客流类型一客控系数Ri及Φ优化流程 图3 大客流类型二客控系数Ri及Φ优化流程

2.2.3 车站大客流控制总体方案优化流程

在上述理论基础上，制定车站大客流总体方案优化流程，具体如下：

Step1 判断车站大客流类型及初始客流预警位置；

Step1.1 加载客流，利用系统动力学仿真模型推演客流在车站内的时空分布；

Step1.2 判断车站大客流类型；

Step1.3 记录初始客流预警位置；

Step 2 根据车站大客流类型及初始客流预警位置，按照2.2.2所述方法进行客流控制系数优化；

Step 3 按照时间序列生成最优客流控制策略，加载原客流进行仿真推演，对该策略客流控制效果进行分析.

3 仿真实验及分析

本文选取福州市某地铁车站为原型搭建车站仿真模型，选取17∶00～20∶00晚高峰时段进站客流调查数据作为输入.仿真设定车站各区域预警启动条件为当该区域客流承载量超过承载能力70%且持续5 min及以上；有效客控措施判定标准为采取该措施后5 min内能够使该区域承载客流量降到安全范围(承载能力80%及以下).主要模型参数设置如表4所示.

表4 主要模型参数设置

3.1 车站大客流类型一客流控制方案优化

该方案仿真场景模拟下车出站客流与进站乘车客流同时持续较大的情况，参数初始化设置如表5所示，客流控制系数初始值设定为R1=R2=R3=0.6，加载进站客流数据，车站各预警区域客流承载量如图4所示.

表5 车站大客流类型一客流控制方案参数初始化设置

由图4可知，若未采取客流控制方案，该车站站台区域、站厅非付费区及站厅付费区将依次于第36 min、第100 min及第120 min启动预警，并将长时间处于客流预警状态，其中三个区域均有超过30 min时间客流量持续达到承载能力极限，严重影响站内客流流动.根据上文2.2所述客流控制方案优化方法及流程，按照时间序列生成客流控制优化策略：在第36 min站台启动预警时，将站厅付费区与站台连接处客流控制系数R1由初始值0.6调整为0.8，在第99 min站厅非付费区启动预警时，实行站外限流，最大进站流量控制在55 人/min.客流控制效果如图5所示.

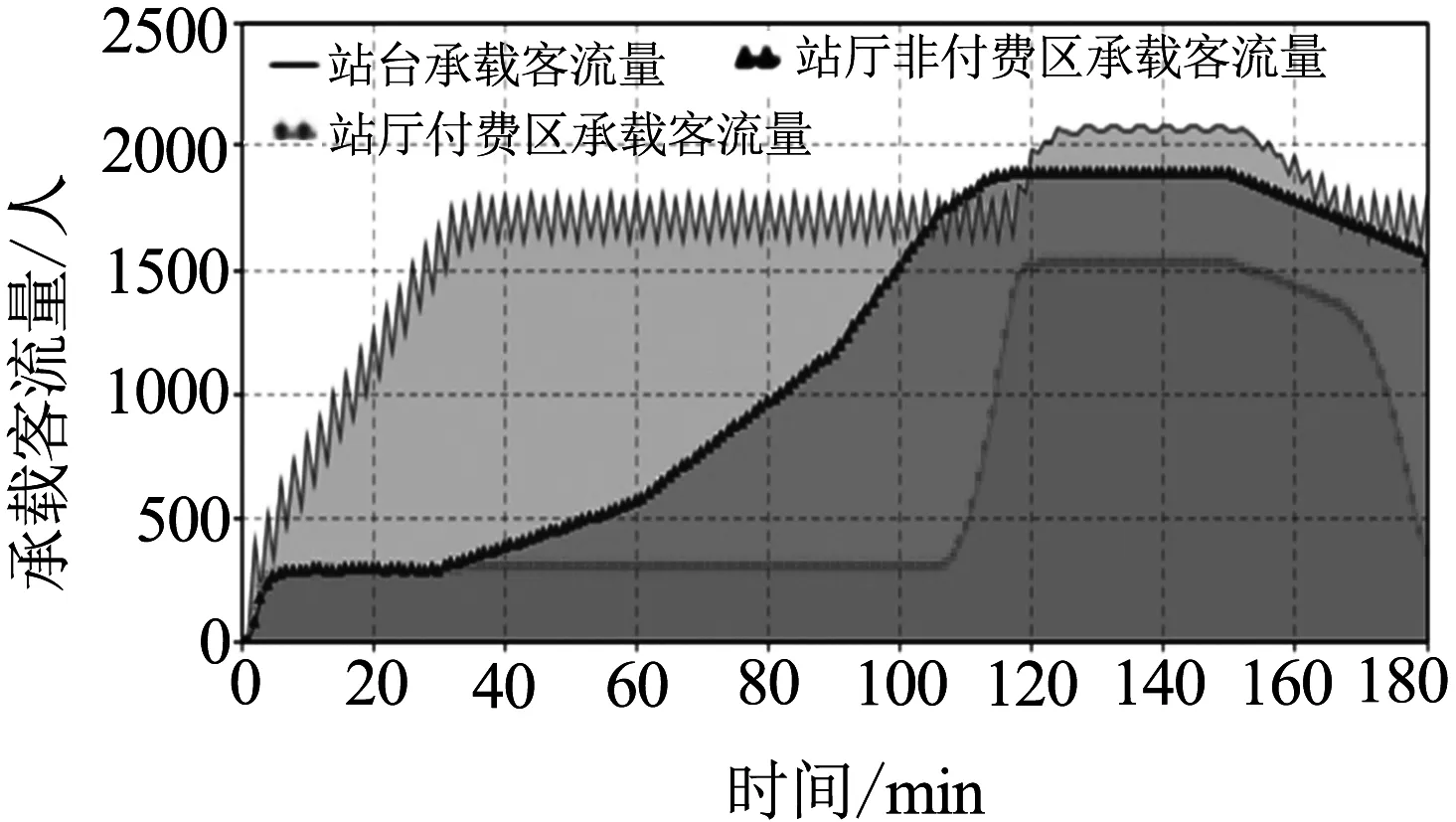
图4 未采取客流控制措施前车站各预警区域客流承载量

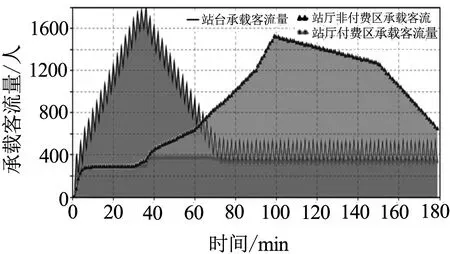
图5 采取客流控制措施后车站各预警区域客流承载量

由仿真结果可知，当采取相应客流控制方案后，站台及站厅非付费区客流承载量均分别达到相应预警值后回落至安全范围，客流得到有效控制的同时确保进站上车总乘客数量最多，车站设施能力得到最大利用.

3.2 车站大客流类型二客流控制方案优化

该方案仿真场景模拟进站客流较大，出站客流较小的情况，参数初始化设置如表6所示，客流控制系数初始值设定为R1=R2=R3=0.6，该车站安检设备保有量为4台，加载进站客流数据，车站各预警区域客流承载量如图6所示.

表6 车站大客流类型二客流控制方案参数初始化设置

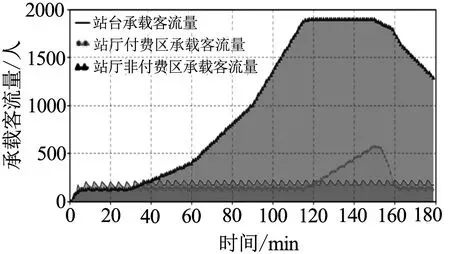
图6 未采取客流控制措施前车站各预警区域客流承载量

由图6可知，若未采取客流控制方案，该车站站厅非付费区将于第105 min启动预警，并将较长时间处于客流预警状态，其中有超过30 min时间客流量持续达到承载能力极限，严重影响站厅非付费区域客流流动.根据上文2.2所述客流控制方案优化方法及流程，按照时间序列生成客流控制优化策略：在第105 min站厅非付费区启动预警时，将安检数量由3台调整为车站最大值4台，在第107 min时，实行站外限流，最大进站流量控制在75 人/min.其客流控制效果如图7 所示.

图7 采取客流控制措施后车站各预警区域客流承载量

由仿真结果可知，当采取相应客流控制方案后，站厅非付费区客流承载量在达到预警值后缓慢回落，车站各预警区域客流承载量保持在安全范围内，同时确保下车客流不受滞留.

4 结论

(1)在前面学者[6-7]研究基础上，进一步梳理并细化了影响车站客流流动的关键要素之间的因果联系，并引入客流控制系数Ri构建车站客流控制模型，相较以往文献，本文在基于系统动力学的车站客流控制模型基础上，进一步提出了客流控制策略优化方法，并最终生成基于时间序列的客流控制策略；

(2)根据现行车站一线广泛采用的三级客流控制基本思路，就不同类型客流提出相应的客流控制方案优化方法，将系统动力学理论与车站工作实践有机融合，仿真结果能够为车站管理人员进行大客流控制提供科学决策；

(3)采用某城市F地铁车站数据进行仿真实验，分别给出了不同客流类型的客流控制方案优化案例，表明研究方法是可行的；

(4)本文所提出的车站客流控制模型适用于普通城市轨道交通车站，由于换乘站大客流成因复杂，其客流控制方案还需结合线网客流控制协调优化做进一步深入研究.