基于响应面法的桥梁节段参数模型修正

许世展，李杨，冯冠杰，张海龙

(1.郑州大学 土木工程学院，河南 郑州 450001；2.中建三局集团有限公司工程总承包公司，湖北 武汉 430000)

有碍于初始建模中存在的结构误差、阶次误差和参数误差，未经修正的初始有限元模型很难真实模拟结构的实际响应[1−2]，在桥梁健康监测、状态评估、车桥耦合振动、抗震分析等精度要求较高的场景中很难应用[3−6]，因此有限元模型修正方法研究是当下的热点问题。现有研究多通过修正敏感性参数来使得目标函数取值最优，其中敏感性参数取值被限定在一定范围内以使其具有明确的物理意义[7−9]，而目标函数则根据桥梁静载测试和动载测试的实测数据进行构造，最终使修正后的模型能准确反映实际结构的刚度、质量、边界、动力特性等信息[10]。在模型修正过程中常用的方法有基于灵敏度修正法和响应面法等，郭力等[11]基于灵敏度修正法，通过复域函数值计算构造参数对目标函数的影响矩阵，考虑有限元模型计算值与实测值之间的误差向量，使用最小二乘法获得参数的最优取值，进行迭代求解，但计算工作量较大；付波等[12]采用响应面法中的CCD试验设计，通过对参数取值和目标函数值的函数拟合，获得两者的显式方程，进行优化求解获得参数的最优取值，该方法具有较高的求解效率；任伟新等[13]以某六跨连续梁为工程背景，采用CCD响应面法进行样本选取、参数修正。与采用灵敏度法相比，响应面法计算精度较高、收敛速度较快，表明基于响应面方法的模型修正具有诸多优势，其在模型修正中的使用日益普遍，然而在既有研究中，选择的敏感性参数以结构整体参数为主，如桥梁整跨结构的弹性模量、质量密度等[6−15]。而混凝土材性参数离散性大，在整个主梁空间范围存在材性差异，尤其涉及施工过程影响时，混凝土材料参数在全桥范围内差异更为明显，钢束应力随其长度形状及张拉力大小不同，结构的材料参数、尺寸、荷载分布等都是具有一定变异性的参数，必然导致桥梁结构在空间范围内的参数差异性存在，在模型修正中选择不考虑材性差异的结构整体参数不能反映实际情况，同时施工监控中的动态模型修正必然选择桥梁结构的节段参数而非整体性参数作为待修正参数，因此研究基于局部参数而非整体性参数的模型修正方法具有重要的理论意义和应用价值。本文以某无背索斜拉桥施工过程为工程背景，选取桥梁结构施工过程中的节段参数为研究对象，采用响应面法进行施工中的动态模型修正，相关方法和结论可为同类工程提供有益参考。

1 响应面法模型修正

1.1 参数筛选原理

参数筛选试验基于数理统计学中的参数估计和统计检验理论，是模型修正的关键环节，用以分析参数影响的显著性程度。现以单参数正交试验为例说明参数筛选的理论依据。参数估计时，假设ξ为φ参数的影响平均值，φi是φ参数i水平影响下对平均值ξ的偏离程度。则ξ和φi的无偏估计如式(1)～(2)所示。

式中：χij为水平φi下第j次试验结果；m为因素φ水平取值个数；n为各水平重复试验次数。

则每次试验结果可以表示成式(3)，反映了参数某水平的影响效应，也反映了误差大小。

判断参数φ对目标函数是否有显著性影响是基于数理统计中的假设检验原理，比较参数水平取值引起的试验结果变动与试验误差引起变动的2个统计量，进行F检验，记Φ为参数水平引起的偏离平均值ξ的组间均方，e为试验引起的组内均方，F检验计算值为式(4)所示。

若F是与1相近的数，则表示这个参数水平的变化对试验结果无显著影响。若F≥1时，一般通过显著性检验表获得F值对应的显著性水平P值，当P＜0.05时表示参数为显著性参数，表明参数对目标函数具有显著性影响的概率保证率在95%以上；当P＜0.01时表示参数为高度显著性参数，这时概率保证率在99%以上。

基于以上参数筛选试验得到待修正的敏感性参数，然后对待修正的敏感性参数进行分析，以显式的响应面模型逼近目标函数与设计参数之间复杂的隐式函数关系，最后对获得的显式响应面模型在实测目标函数值内做最优化求解[14−17]，获得待修正敏感性参数的修正值。响应面模型可采用2阶模型来逼近，如下式所示：

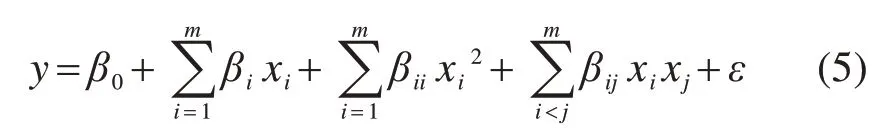
式中：βi表示xi的线性效应；βii表示xi的2阶效应；βij表示xi与xj的交互作用效应。

1.2 模型修正流程

模型修正流程如图1所示，首先建立全桥的初始有限元模型，初始模型的参数取值、边界模拟、结构尺寸等均采用设计值，然后对初始模型的结构误差、阶次误差进行判断；其次进行参数筛选试验，通过Plackett-Burman(P-B)试验筛选出显著性参数(P-B试验可用最少的试验次数达到快速筛选显著性参数的目的，但不能区分参数的主效应与交叉项的影响[18−19])，根据显著性参数对目标函数的影响程度确定待修正参数类别；基于现场实测数据确定目标函数类别，据此制定模型修正的响应面法方案，通过对响应面模型的优化求解得到待修正参数的最优取值。

图1 施工阶段模型修正流程图Fig.1 Construction stage model updating flow chart

2 初始模型

2.1 工程背景

某波形钢腹板无背索斜拉桥跨径布置为35+60 m，桥梁立面如图2所示，索塔采用预应力混凝土结构矩形截面形式，塔高53.7 m，塔身水平倾角57°。主梁采用分离式单箱双室波形钢腹板箱梁，如图3所示，其中波形钢腹板采用厚16 mm的1200型号。斜拉索为7根平行钢绞线索。施工监控过程中选择结构重要位置设置变形、应力测点，主跨跨中B1及根部B2截面设置正截面应力测点，测点位置如图3所示；斜拉索S4与主梁顶板锚固位置设置变形测点P1，主塔2号块和3号块界面位置设置正应力测点T1，主塔施工节段设置11个变形测点C1～C11。该桥采用先满堂支架施工主梁，后分节段液压爬模施工主塔的施工步骤，详细的施工阶段信息如表1所示。

表1 施工阶段信息Table 1 Construction phase information

图2 桥梁立面布置图Fig.2 Layout of bridge elevation

图3 箱梁截面及应力测点布置图Fig.3 Box girder section and stress measuring point layout drawing

2.2 初始有限元模型

波形钢腹板组合箱梁结构采用三维有限元建模，C55混凝土翼缘板采用Solid45单元模拟，Q345C材料钢腹板和塔柱钢横梁采用Shell181单元模拟，Shell181单元与Solid45单元间通过嵌入式共节点或约束方程实现约束连接。Strand1860钢绞线预应力钢束采用link10单元模拟，link10单元与混凝土Solid45单元间使用CP命令或共节点方式建立耦合关系，依据规范计算施工阶段短期预应力损失在初应变中折减扣除后加以考虑[20]。平行钢绞线斜拉索模拟为只受拉杆单元，建立的有限元模型如图4所示，共189 876个单元，228 230个节点，桥梁结构的材料参数按规范及设计取值。施工阶段模拟时，索塔节段湿重和爬架模板自重等效为竖向节点荷载，满堂支架模拟为只受压杆单元，施工结构的体系转换通过单元的生死功能实现，结构的收缩徐变效应采用等效降温法和根据按龄期调整的有效模量法调整金属蠕变系数的方法实现。

图4 全桥有限元模型Fig.4 Full bridge finite element model

3 施工阶段有限元模型修正

根据图1所述的施工过程模型修正流程图逐步进行模型修正。由于施工监控中的模型修正是一个动态过程，其间要经历多次的误差识别及参数修正，鉴于篇幅所限，本文仅以斜拉索S4张拉后施工阶段模型修正过程为例，说明多参数模型修正的关键技术环节。

3.1 参数筛选试验

采用P-B试验筛选显著性参数，其中目标函数设定为该施工阶段具有现场实测有效数据的6个关键监测数据，即R1—B1跨中截面正应力，R2—B2根部截面正应力，R3—B1跨中截面竖向变形，R4—主塔悬臂7号块(斜拉索S4张拉后对应的桥塔施工节段)端部纵桥向变形，R5—主塔悬臂7号块端部竖向变形，R6—T1主塔根部截面正应力。根据规范及相关文献得到对目标函数可能存在影响的11个参数的变异性分布[6−15,20−24]，参数可能的取值范围如表2所示。

表2 待筛选参数Table 2 Parameters to be filtered

待筛选参数的个数为11，选用样本个数为12的P-B试验，将每一样本方案进行一次有限元模型计算，共计算12次，得到6个目标函数的计算结果，进行显著性参数方差分析，若参数对目标函数R1～R6概率保证率在95%以上则判断为显著性参数，在此基础上拟合出显著性参数与6个关键目标函数间的显式关系一次多项式回归方程，如式(6)～(11)所示。

采用式(6)～(11)中参数系数与常数项的比值作为影响程度系数并记作λ，用以衡量参数变化对目标函数的影响程度，计算结果如表3所示。表中影响程度系数λ为“−”时，表示参数为非显著性参数，同时将参数系数除以参数系数最大值得到引入归一化影响参数κ，基于监控可取的精度条件，将κ大于0.2作为影响程度较大的参数加以修正。

表3 修正参数影响程度结果Table 3 Results of influence degree of updating parameters

3.2 CCD试验拟合响应面方程

结合当前施工阶段的现场实测数据及误差分析结果，选取R4和R6作为目标函数，待修正参数根据表3确定，参数取值范围由表2确定，进行4参数、2目标函数的5水平、21试验样本的中心复合设计试验(CCD)，待修正参数均为新增结构节段参数，计算目标函数结果。根据中心复合设计试验结果，对参数的交叉项和平方项进行显著性分析，显著性水平取α=0.05，对应F值为3.2，方差分析的显著性结果如图5所示，根据分析结果可知，高次项K2对目标函数R4和R6有显著性影响。

图5 不同参数对目标函数显著性分析Fig.5 Significant analysis of different parameters towards objective functions

基于以上分析拟合出目标函数与待修正参数的显式响应面方程如式(12)～(13)所示。经验证，式(12)～(13)在当前施工阶段中具有较高的拟合精度。

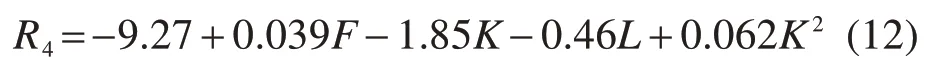
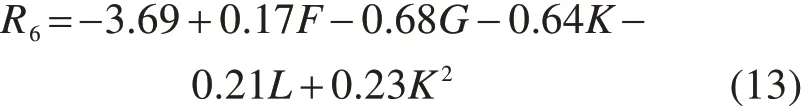
3.3 有限元模型修正

将现场监控实测的目标函数数据代入显式方程式(12)～(13)中优化求解，得到待修正参数最优取值如表4所示。

表4结果显示，修正后的主塔质量节段密度(F)增加0.74%，结合立模情况，当前混凝土浇筑后模板变形较小，结构立模尺寸精确，主塔节段质量接近施工图设计值，偏差较小。修正后的主塔预应力(G)增大1.17%，修正后的斜拉索索力(K)增加4.26%，受张拉时操作人员水平及其他多种因素影响，该误差客观可能发生，索力张拉误差在规范允许偏差范围内；修正后的斜拉索弹性模量(L)增大4.04%，符合参数变异范围要求。将修正后的参数代入有限元模型中计算分析可知，主塔悬臂端头顺桥向位移计算值与实测值间的偏差由5.94%减少到1.98%，主塔根部应力计算值与实测值间偏差由修正前的8.98%减少到1.49%，模型改进效果明显。

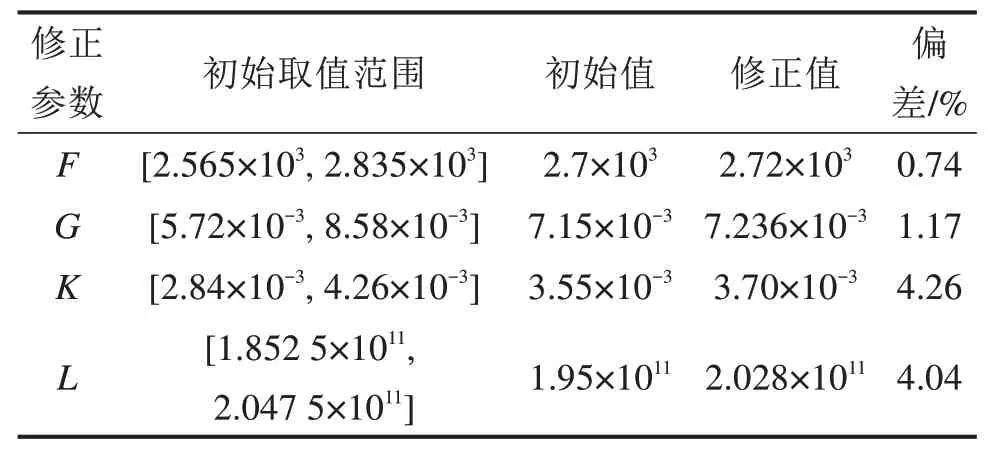
表4 修正参数设计取值范围及修正结果Table 4 Updating parameter design value range and correction result

采用修正后的模型继续进行施工监控，并对后续施工阶段中预测值与实测值有较大偏差的情况进行同样的处理，保证施工监控模型始终与实际结构相吻合，采用此方法，施工监控完成后，桥梁成桥状态达到设计要求，与设计目标相比最大线形误差值为1.1%，结构关键截面R1～R6数据实测值与最终模型计算值吻合较好。

4 结论

1)基于Plackett-Burman试验的参数筛选试验可以较为便捷地在大量参数中快速筛选出对目标函数有显著性影响的参数，并初步给出显著性参数的影响程度系数，帮助确定待修正的参数类别，是多参数模型修正的有利工具。

2)施工监控中的动态模型修正时，选择节段参数作为待修正参数可以获得更好地修正模型，通过施工过程中的多次模型修正，可以使模型参数修正中利用到更多的监测数据，获得更为准确的修正模型。

3)根据无背索斜拉桥成桥状态监测数据的对比分析，采用节段参数结合响应面法的动态模型修正技术，可以准确把握桥梁施工状态，精确指导下一阶段施工，保证整个施工监控过程的控制精度。