近地星座异面遍历交会轨道全局优化
黄岸毅,罗亚中,李恒年
(1. 西安卫星测控中心宇航动力学国家重点实验室,西安 710043;2. 国防科技大学空天科学学院,长沙 410073;3. 空天任务智能规划与仿真湖南省重点实验室,长沙 410073)
0 引 言
随着互联网星座等大型星座的发展,低轨空间在轨服务技术的重要性越来越突出。通过在轨服务,可以对卫星进行部件维修、燃料加注等操作,显著提高卫星寿命,降低发射成本。对于大型星座中多颗卫星需要维护的情形,在轨服务航天器在任务实施前需要规划出合理的交会次序和飞行时长,以实现任务收益最大化。因此,规划算法要能够尽可能以高效率收敛到接近全局最优解。
当前这类包含整数规划和实数规划的混合规划问题求解存在的主要困难是计算目标函数的效率不高,导致优化算法收敛缓慢。目标函数一般设计为速度增量最小(或者等价指标燃料消耗最小),当考虑近地轨道摄动时,预估轨道交会所需的速度增量较为困难。如果采用轨道根数差分形式,将升交点赤经差对应的法向脉冲和相位差对应的切向脉冲直接叠加,或采用二体解析模型获得多脉冲交会的近似解,由于未考虑摄动,误差会很大,且需要对脉冲位置进行寻优,效率偏低。数值优化方法需要建立包含每个脉冲大小和时刻的优化模型,调用进化算法求解,计算耗时难以满足混合整数规划期间大量调用计算的需求。因此合理的交会速度增量解析估计方法是解决这类规划问题的关键。
对于近地长时间轨道交会问题,利用摄动影响升交点赤经长期漂移的规律,可以通过漂移率间接控制实现轨道面的重合。文献[13]将该原理应用于星座部署的优化设计,对漂移轨道的参数进行离散化和遍历寻优。这些研究没有完全揭示漂移率控制和瞬时直接控制在速度增量消耗上的规律,无法解析得到最优的机动策略,准确度不够高。Huang等利用半解析的等式约束优化方法建立了升交点赤经直接控制和漂移率控制混合策略的最优交会近似估计模型,总速度增量估计精度较高,但其中四脉冲的计算都使用了圆轨道假设,在机动量较大时每个脉冲的大小存在一定偏差。
本文根据星座中卫星之间轨道高度和倾角相同的特性,将文献[14]提出的方法简化为仅考虑升交点赤经差和相位差,通过两次双脉冲霍曼变轨实现从初始轨道至漂移轨道以及从漂移轨道至目标轨道的转移,代替了文献[14]中根据轨道根数差和圆轨道近似计算脉冲大小的过程,使得四个脉冲的计算更精确。在此基础上,建立了多星交会混合整数规划模型,并应用混合编码遗传算法求解,整体规划效率较高。采用文献[4]中算例进行分析对比,本文算法获得指标有显著提高。
1 LEO星座服务遍历交会轨道优化问题
本文面向的星座类型为近地Walker星座,特点为所有卫星的轨道参数中仅升交点赤经和相位互不相同,且仅考虑轨道倾角不为0、偏心率近似为0的情形。假设星座中部分卫星发生故障或燃料消耗殆尽,需要由在轨服务航天器依次交会这些卫星并开展维护作业,此时就要寻找一条最优交会序列及路径,使得服务航天器在给定的任务约束下,以最少的燃料消耗完成任务,如图1所示。
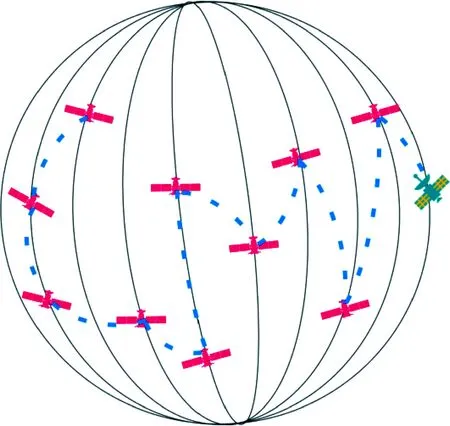
图1 多轨道面星座遍历交会路径
服务航天器采用脉冲推进方式,交会一颗卫星后消耗一定时间进行服务操作,然后离开并开始与下一颗卫星交会。任务约束一般包括任务总时长约束、交会停留最小时长约束、总燃料最大值约束等。
该问题需要求解每次交会目标的顺序和交会时刻(等同于交会转移时长)。对于这个混合整数规划问题,关键是快速准确地计算服务航天器从一个目标交会下一目标的速度增量。解决了这一问题,任务代价也即目标函数就可以快速评价,从而应用各类通用的混合整数规划算法进行全局优化。
2 圆轨道同倾角摄动交会脉冲快速计算
目标到目标之间的脉冲交会问题可以描述为:已知出发轨道和目标轨道半长轴、倾角相同,分别为和,初始升交点赤经和纬度幅角为和,目标升交点赤经和纬度幅角为和,给定交会飞行时间Δ,求解轨道交会所需的最优速度增量。
2.1 漂移轨道组合策略
方法基本思想如下,根据摄动一阶分析理论,摄动引起圆轨道半长轴、倾角、升交点赤经和纬度幅角的长期变化率为:
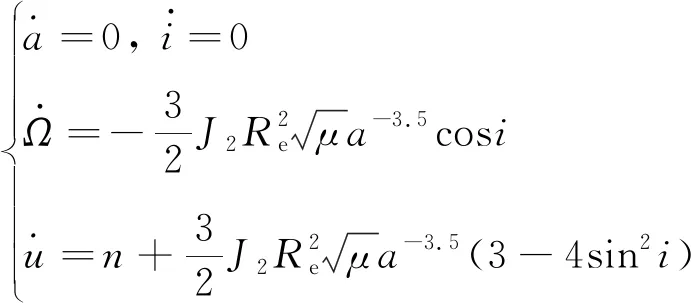
(1)
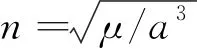
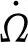

图2 漂移轨道和霍曼转移示意图
2.2 满足Ω约束的脉冲近似最优解
设终端时刻转移航天器轨道根数和目标轨道根数有升交点赤经差Δ=-。设漂移轨道的半长轴和倾角相对圆轨道偏差为未知量Δ和Δ,则转移到漂移轨道的两脉冲霍曼变轨前后的速度大小为:

(2)
式中:为初始圆轨道速度大小,为第一个脉冲后的速度(椭圆轨道近地点),为第二个脉冲前的速度(椭圆轨道远地点),为第二个脉冲后的速度。设起漂阶段对升交点赤经的直接改变量为Δ,则起漂阶段对轨道面法向量的角度改变为

(3)
将Δ等分为和作为法向脉冲加入霍曼变轨中,由图3的几何关系可得,霍曼变轨的两个脉冲Δ和Δ(,,与Δ的关系类似)分别为:

图3 脉冲前后速度矢量
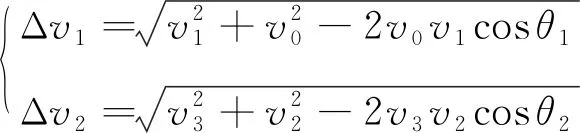
(4)
由漂移轨道控回初始轨道半长轴及倾角时,将升交点赤经直接改变量同样置为Δ,即总的脉冲对轨道半长轴及倾角的改变量为0,对升交点赤经的改变量为2Δ。则对于给定Δ, Δ和Δ,建立漂移轨道和恢复初始轨道所需的总速度增量为
Δ=2(Δ+Δ)
(5)
漂移轨道需要满足升交点赤经约束:
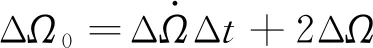
(6)
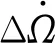

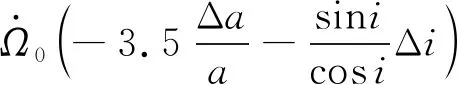
(7)
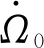
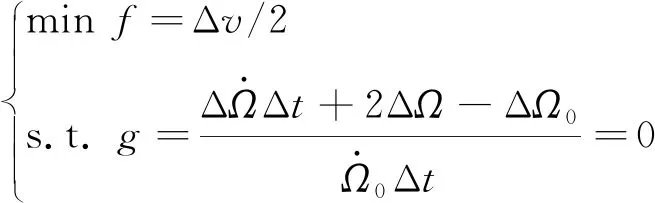
(8)
令=+,则根据极小值原理,最优解应满足:
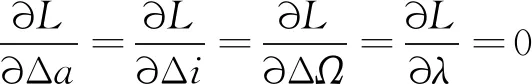
(9)
展开得方程组:
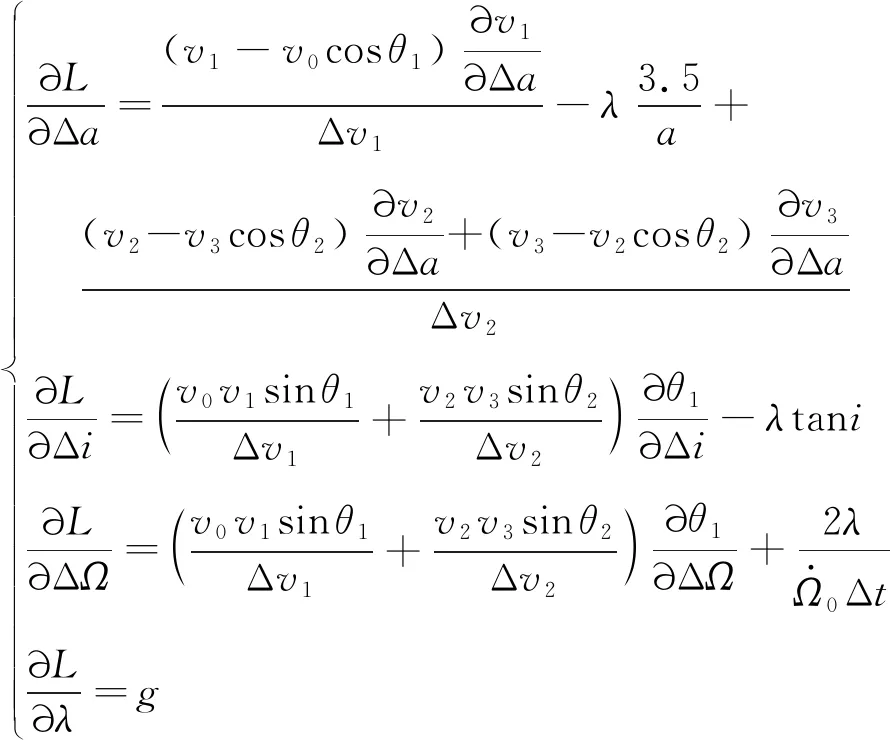
(10)
式中:
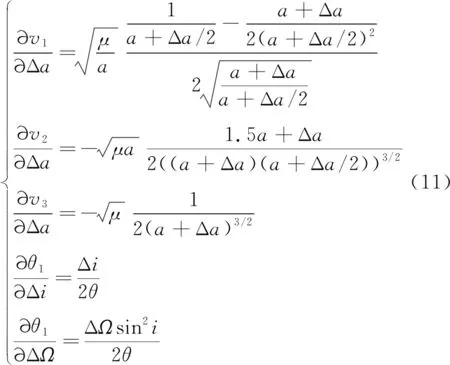
利用文献[14]中的近似解作为初值:
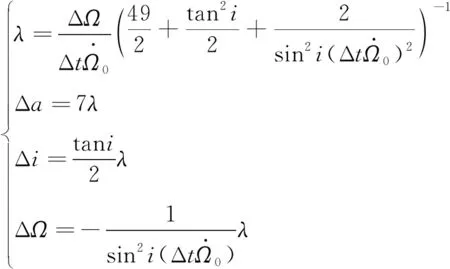
(12)
使用一种非线性方程求解工具包Minpack简单迭代即可得到最优解,记为Δ,Δ和Δ。
2.3 满足u约束的脉冲修正解

(13)
式中:Δ′应归一化到[-π,π]。为了满足交会约束,需要修正Δ。根据相位漂移率与半长轴的关系可得修正量Δ为:
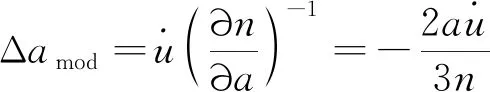
(14)
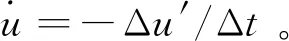
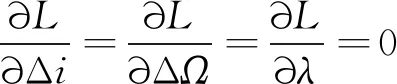
(15)
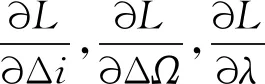
综上,根据初始轨道和目标轨道的升交点赤经差Δ和相位差Δ,即可通过先后求解式(10)、式(14)和式(15)得到速度增量的近似估计值以及漂移轨道相对初始轨道的半长轴差、倾角差和升交点赤经差。
3 混合整数规划模型与求解
本文的轨道交会优化问题需要求解的变量为:使得总速度增量最小的交会次序(整数规划)以及在目标两两之间的转移飞行时长(实数规划)。这是一个混合整数规划问题即时间依赖旅行商问题,可使用混合编码的遗传算法(GA)进行优化。
设目标个数为,则优化变量={}的维数设置为2。其中前个值用来编码目标两两之间的转移时间(取值为0到1的实数),后个值用来编码目标的顺序(取值为1到的整数)。航天器在目标两两之间的转移时间表示为:
Δ=Δ+(Δ-Δ)
(16)
式中:Δ,Δ分别为任务约束的最短和最长转移飞行时间。交会时刻表示为:
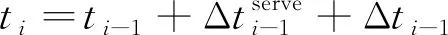
(17)
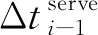
据五建公司副总工程师王永科介绍,无轨导全位置爬行焊接机器人能实现焊接过程中对焊缝的实时扫描及跟踪,运动过程中无需轨导引,利用磁性吸附和电机驱动功能能够沿直线、弧线等曲面实现自动爬行,同时避免了有限空间和危险场所人工焊接不便和危险性,可以有效提高焊接质量和效率。
设Δ为第段转移的速度增量,目标函数一般取为总速度增量:
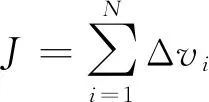
(18)
利用GA求解,通过种群初始化和逐代进化,最后可得最优的交会次序和交会转移时长。具体流程此处不再赘述。
4 仿真算例
4.1 速度增量与交会时间和轨道根数差的关系
设轨道为半长轴7100 km、倾角98°的圆轨道。初始轨道和交会轨道只存在Δ为5°,转移时长为7天时,本文计算得到的交会脉冲总和为440.3 m/s。每组霍曼变轨双脉冲大小分别为111.1 m/s(近地点)和109.1 m/s(远地点)。作为对比,文献[14]中估计结果为444.1 m/s,每个脉冲均为111.0 m/s。这是因为仅使用圆轨道假设时,近地点处脉冲估计值偏大,远地点处脉冲估计值偏小。文献[14]针对的轨道需兼顾小偏心率情况,无法应用霍曼变轨双脉冲计算。而本文针对的是同圆轨道之间的转移,霍曼变轨能够提高单个脉冲估计精度。
利用估计方法对交会速度增量与Δ,Δ和Δ的关系进行定量分析。当Δ为5°时,对应不同转移时长的Δ变化趋势以及速度增量中用于改变半长轴、倾角、升交点赤经的分量如图4所示。初始轨道和交会轨道只存在Δ为180°时,对应不同转移时长的Δ变化趋势以及各分量如图5所示。
可见当Δ较小时,改变升交点赤经漂移率的累积时间较短,最优策略更倾向于利用法向脉冲直接改变升交点赤经的方式实现交会(图4中虚线,随着Δ增大显著下降);而当Δ较大时,最优策略更倾向于改变升交点漂移率的方式实现交会(图4中点划线和点线,随着Δ的增大在速度增量中占比变大),升交点赤经的直接改变量占比非常小。
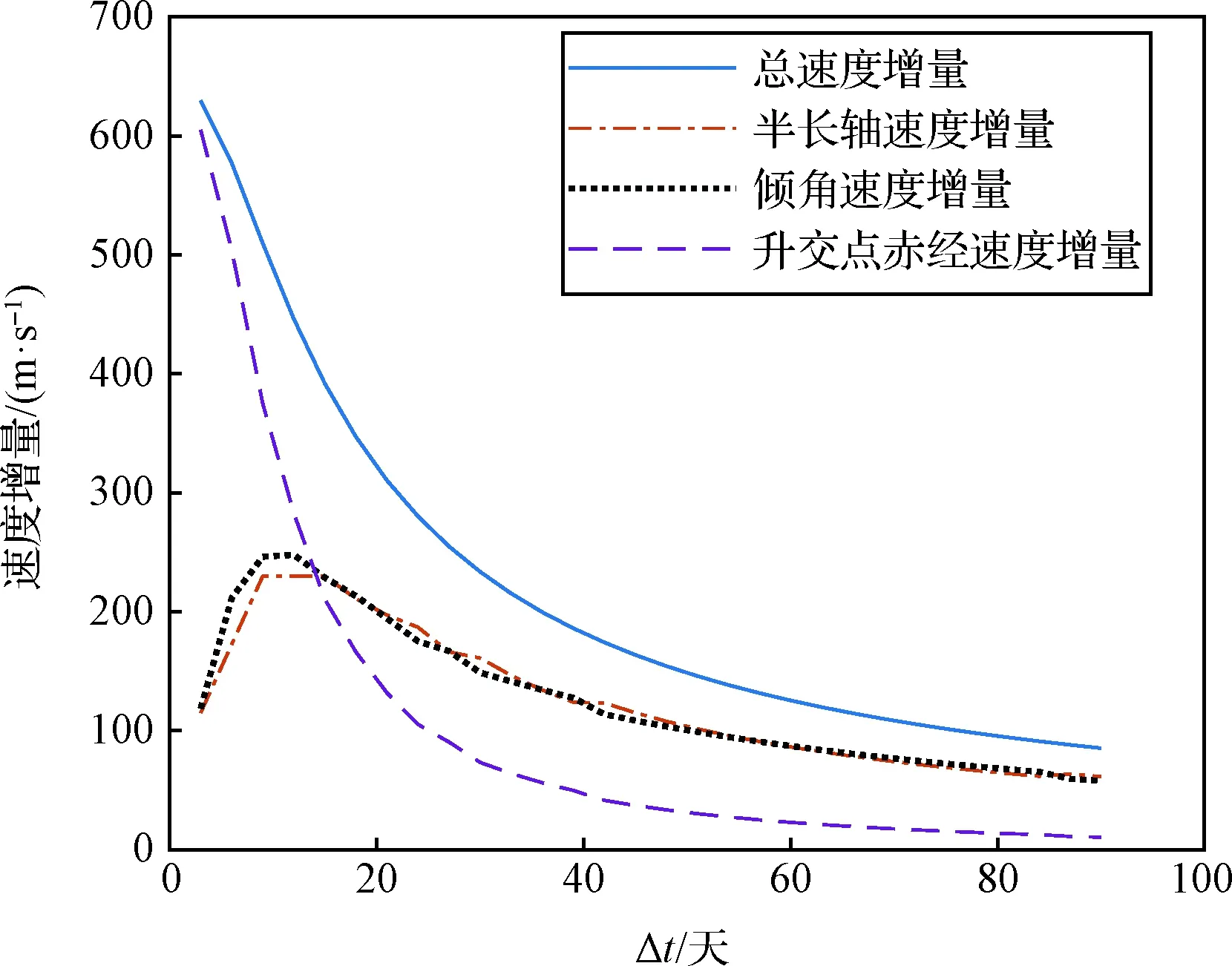
图4 给定ΔΩ0时速度增量与转移时长的关系
Δ所需的速度增量同样随着转移时长增大而逐渐减小,且在相同转移时长下,每度相位差所需的速度增量远远小于每度升交点赤经差。这也证明了本文首先根据升交点赤经差计算控制量(式(10)),然后在解附近根据相位约束进行修正(式(14)和式(15))的思路是正确的。此外还可以看到,由于摄动的影响,调相对半长轴的改变会引起升交点赤经的耦合漂移,因此还是需要一部分面外机动量(图5中点划线和点线)抵消这部分摄动漂移量。

图5 给定Δu0时速度增量与转移时长的关系
对比单纯法向脉冲1°升交点赤经需要约130 m/s速度增量,通过升交点赤经漂移策略能够显著降低Δ。从图4和图5中各分量的变化趋势来看,当Δ较大且允许的转移时间较短时,最优交会速度增量Δ主要取决于Δ,相位差Δ的影响要小一个数量级,此时多星交会的最优次序应当与升交点赤经的排列顺序一致;而当Δ较小且转移时间较长时,最优交会速度增量Δ中Δ与Δ的影响量级接近,此时最优交会路径就需要全局优化计算。下面用两个多星交会算例进行验证。
4.2 轨道面大幅度变化的交会序列优化
目标航天器分布在8个轨道面(半长轴7100 km,倾角98°,偏心率0),有11颗星需要交会,轨道根数见表1。两两之间的最长转移时间为60天,停留时间为0,脉冲推进比冲为407.9 s。追踪航天器初始升交点赤经和纬度幅角为0。
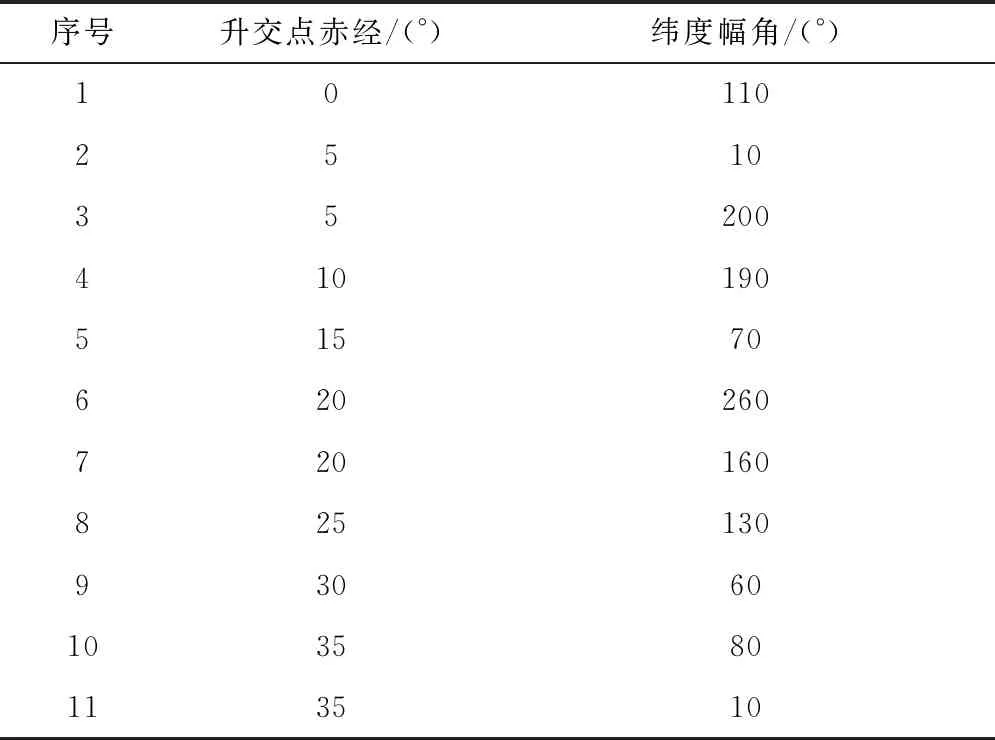
表1 目标轨道参数
GA参数设置见表2,交会最优序列和速度增量消耗见表3。

表2 GA参数
总速度增量为887.62 m/s,最优交会序列沿着赤经从小到大的路径,且最优交会时长均为容许最长时间,这也与4.1节的分析吻合。同时表3还列出了文献[14]方法得到的速度增量以及使用文献[19]基于进化算法的四脉冲优化方法得到的最优解,可见本文估计结果更接近进化算法,但差别较小。本文方法单次估计耗时0.18 ms(CPU:4.2 GHz),小于文献[14](1 ms)和进化算法(600 s以上)。
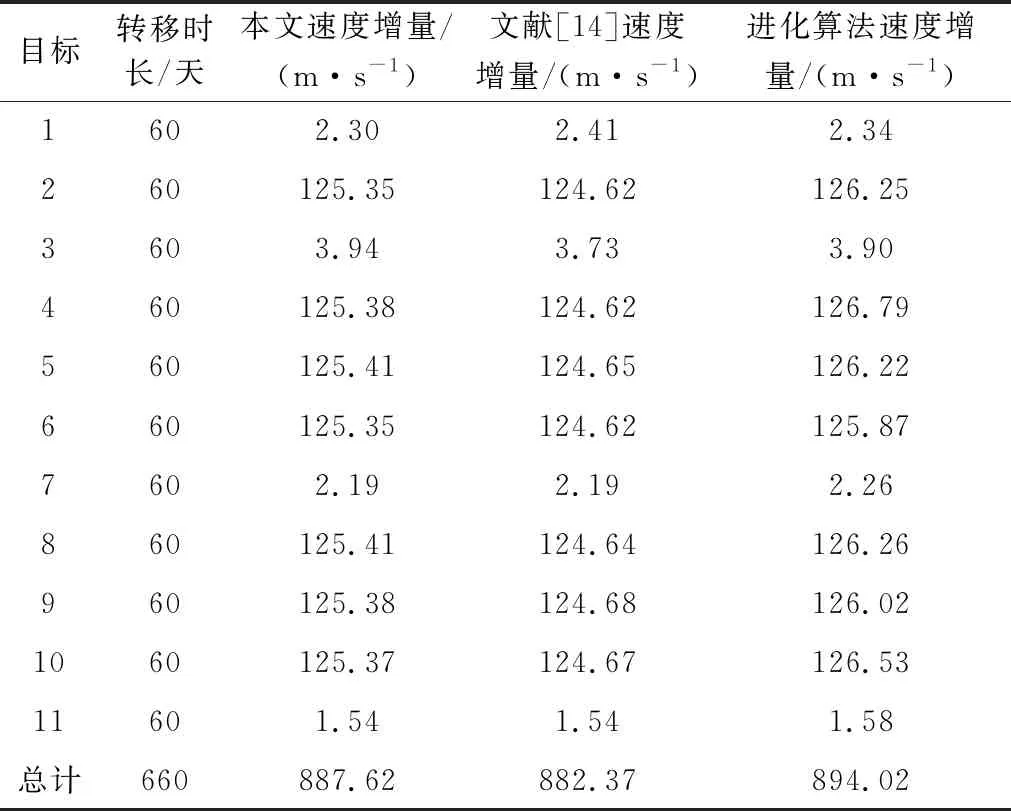
表3 最优交会路径
4.3 轨道面小幅度变化的交会与重构路径优化
该算例来源于文献[4],1颗服务航天器交会8颗无剩余燃料的目标卫星。与4.1节交会任务略有不同的是,服务航天器最大转移飞行时长为600(为标称轨道周期),在交会每个目标卫星后需要停留一定时间(10到600之间),且为目标加注燃料(100 kg+自身重构机动所需燃料)。自身重构机动是指每个目标卫星在加注完成后即开始机动,将自身的轨道面和相位重新调整到预定的8个位置之一,最终使8颗卫星形成完整星座构型。
其设定的目标互相之间升交点赤经偏差较小,属于共面星座长期摄动产生的偏差,此时轨道面调整和相位调整所需的控制量相近,交会路径更需要进行全局优化。因此,待优化变量维数是4(目标个数=8)。其中增加维变量以描述交会后停留的加注时长(实数),另外维变量描述每个目标卫星在完成加注后需要到达的星座轨位的序号(整数)。任务优化指标为航天器初始质量,可根据航天器结构质量、任务过程中消耗的燃料质量以及为星座加注的燃料质量递推计算:

(19)
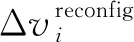
服务航天器轨道高度为7792.137 km,倾角52°,偏心率为0,初始升交点赤经为100°,纬度幅角20°。目标星初始轨道高度和倾角相同,其它根数见表4。
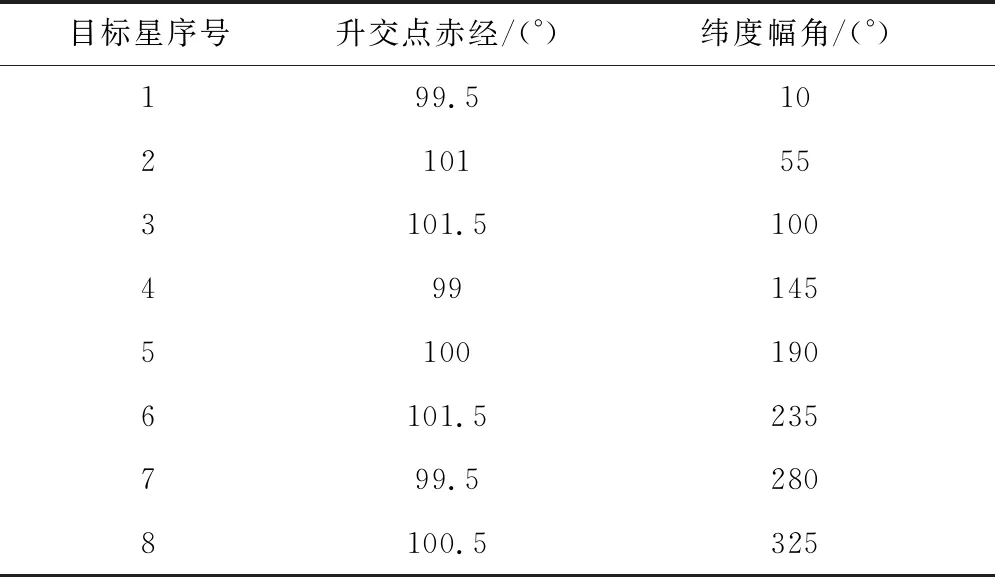
表4 目标星轨道参数
对应的优化结果如表5~6和图6所示。平均单次服务消耗燃料为4.432 kg,与文献[4]中8.333 kg的结果对比,燃料消耗降低了约46.8%。文献[4]中最优交会路径为1-7-4-5-8-2-3-6,本文最优路径为7-4-1-5-8-2-3-6。

图6 服务路径及重构路径

表5 文献[4]的优化结果
算法在普通电脑上运行约5 min即可收敛到最优解。本文使用多脉冲估计模型替代了原文献中的双脉冲近似模型,且不需要对飞行圈数进行遍历寻优,因此优化性能和效率得到很大提高。
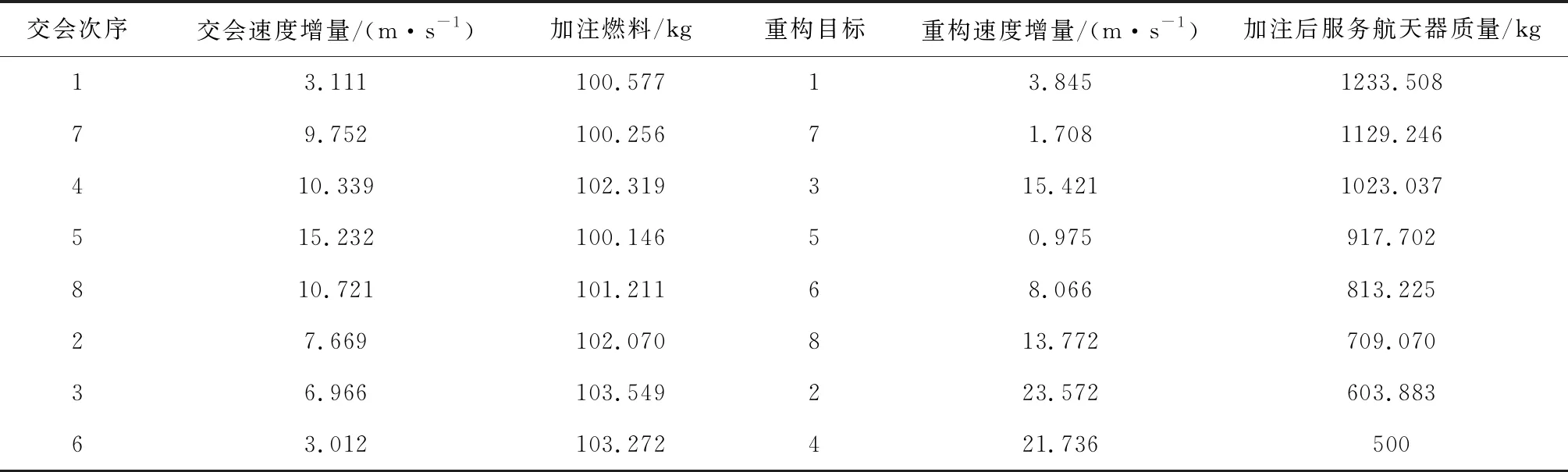
表6 本文获得的最优解详情
5 结 论
本文设计了一种轨道高度和倾角相同时基于升交点赤经漂移轨道的异面交会组合机动策略,通过等式约束优化方法获得最优四脉冲解。利用这种快速脉冲求解方法建立了多星交会序列的混合整数规划模型,通过遗传算法获得交会次序、交会时刻的最优解。仿真算例证明本方法规划求解耗时短,且结果更优。可适用于近地在轨服务、星座构型重建等任务的快速优化设计和分析。

