一种不依赖剩余时间估计的巡航导弹多约束制导律
王宁宇,王小刚,白瑜亮,崔乃刚,李 瑜
(1. 哈尔滨工业大学航天学院,哈尔滨 150001;2. 北京空天技术研究所,北京 100074)
0 引 言
在现代作战场景下,巡航导弹作为对地面静止或慢速移动目标精确打击的有效武器,相较于易于被预测的弹道导弹,具有射程远、机动能力强、突防效果好、命中精度高、毁伤效果好等特点。近年来,美、俄、法等国对于巡航导弹开展了大量研究并取得了诸多代表性成果。美国在2013至2015年间多次试飞新一代巡航导弹,实现途径航路点、规避障碍、精确打击等任务,并演示了在线规划算法。俄罗斯与印度联合研发了“布拉莫斯”巡航导弹,并于2015年军演中精确命中退役舰船“阿勒皮”。法国的“飞鱼”巡航导弹同样是在多次战争中屡建战功。
随着现代战争的兴起,仅满足终端脱靶量要求的制导律设计越来越不能满足现代海战的需求。巡航导弹在保证传统等高等速飞行约束的前提下,同样需要保证一定的末端打击角度来提高导弹对目标的毁伤效果;同时为实现导弹协同饱和攻击,如何控制导弹能够同时到达目标同样成为提高打击能力的关键因素。为有效提升巡航导弹自身的突防能力,实现多巡航导弹编队完成突防任务,往往需要考虑打击时机的选取和攻击角度的控制,因此关于时间约束和攻击角度约束的制导律成为各国争相研究的热点。
国内外众多学者针对末端角度约束制导律的设计进行了深入研究,对于末端角度约束制导律的设计已经相当成熟。Tsalik等将圆弧轨迹的概念引入到相对运动方程,针对静止目标提出了一种角度约束的最优偏置制导律。Hu等将滑模变结构算法引入到制导律设计过程中,设计出一种“滑模+最优”的两阶段角度约束制导策略。不同于传统垂直平面内末端角度约束制导律设计,文献[10]基于三维耦合作战场景,结合双曲正切函数特性推导了一种针对静止地面目标的非线性反演制导策略。针对于机动目标,文献[11]将深度学习引入到角度约束制导律设计过程中,提出一种基于深度强化元学习和剩余飞行时间感知逻辑函数角度约束的三维制导律。
为了更好地提升对目标的协同打击能力,增强对目标的毁伤效果,越来越多的研究人员开展了末端角度/时间双重约束制导律的研究。Chen等通过精确估计角度约束制导律的剩余时间,设计期望时间和剩余时间误差反馈控制器,得到了一种既考虑打击时间又考虑末端角度约束的制导律。Yan等针对三维静止目标,通过对带有末端角度约束飞行轨线的剩余时间进行估算,提出了一种考虑时间和角度约束的弹道成型制导律。文献[14]基于最优控制理论对剩余时间进行精确估计,以此为基础设计了一种同时控制时间和末端角度的三维混合制导律。
综上,目前国内外对于攻击角度和攻击时间约束制导律开展了深入研究,但大多需要在剩余时间精确估算的前提下开展打击时间约束制导律研究,其剩余时间估算的准确与否直接影响到最终时间约束制导律的精确性,文献[15]首先提出不考虑精确剩余时间估算的时间约束制导律设计。在真实强干扰战场环境下,对于剩余时间难以进行精确估计,因此需要开展不依赖剩余时间精确估算的攻击角度/时间约束制导律的研究,从而设计更能适应真实战场环境的多约束制导律。
针对巡航导弹末端多约束制导律需要解决的剩余时间估计误差大的难题,本文通过推导航向相对运动方程,得到了航向平面最优制导律;通过设计基于飞行时间误差的指数型附加航向角,推导出一种不依赖剩余时间估计的航向角度/时间最优制导律;通过在线求解时间增益系数保证导弹能够按照期望时间对目标进行精确打击,并基于不同期望打击时间实现弹道的在线自适应机动。接下来通过求解常规偏置导引律的闭环轨迹方程,给出制导律收敛初始条件。最后,通过仿真验证了本文提出算法的正确性和有效性,并针对不同初始条件和不同末端约束作战场景进行了制导律适应性验证。
1 巡航导弹运动数学模型
在不考虑地球自转和地球曲率的情况下,巡航导弹主要受到推力、空气动力、重力作用,为实现本文大航程航向制导律设计,采用位置坐标系下的三维运动模型,如下:
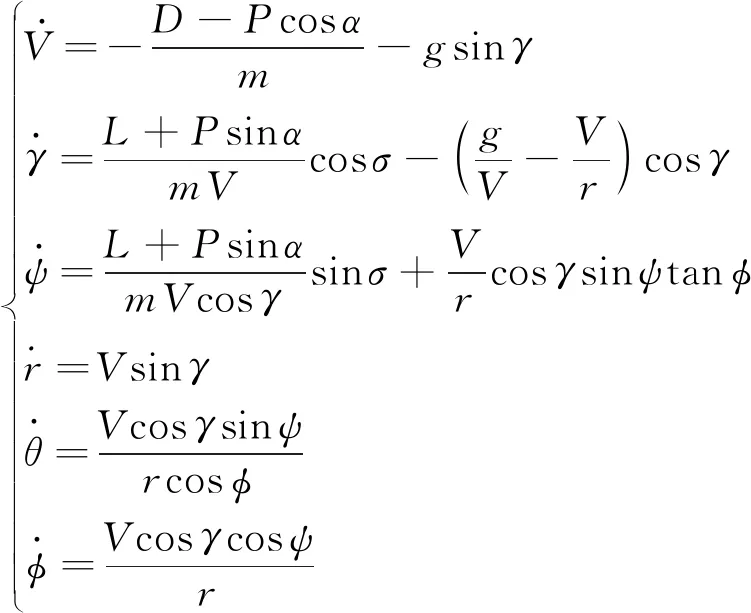
(1)
式中:为速度;为飞行路径角;为巡航导弹质心到地心的距离;为航向角;为经度;为纬度;为推力;为攻角;为倾侧角;为阻力;为升力;为地球引力加速度。
阻力和升力的计算方式采用:
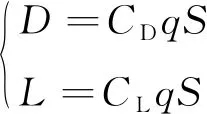
(2)
式中:为巡航弹特征面积;=/2为飞行动压,其中为大气密度,采用常规大气密度公式计算:
=exp(-)
(3)
式中:=141×10m与=1225kg/m为常系数;=-为飞行高度,其中为地球平均半径。
式(2)中和分别为阻力系数和升力系数,采用如下经验公式:
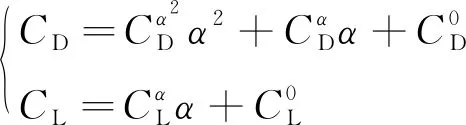
(4)
图1给出了巡航导弹飞行过程中的弹目相对运动关系,其中,表示巡航导弹;表示打击目标点;表示巡航导弹的飞行速度;表示平均地球半径大小为6371.001 km;和分别表示巡航导弹飞行过程中的经度和纬度;和分别表示目标点的经度和纬度;表示期望航向攻击角度;表示巡航导弹剩余射程;为航向视线角表示弹目连线与北向的夹角;表示弹目连线在地球上的投影与地心形成的地心角;航向速度前置角Δ为视线角和航向角的差值,表示为:

图1 弹目相对运动关系图
(5)
因此根据俯仰平面内的相对运动方程,可推导得到航向平面相对运动方程如下:
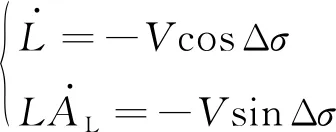
(6)
弹目地心角和视线角采用球面三角形公式计算:
=arccos(sinsin+
coscoscos(-))
(7)
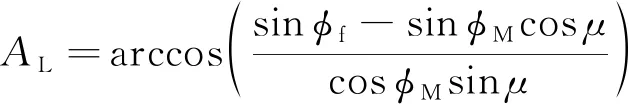
(8)
推力表达式为:
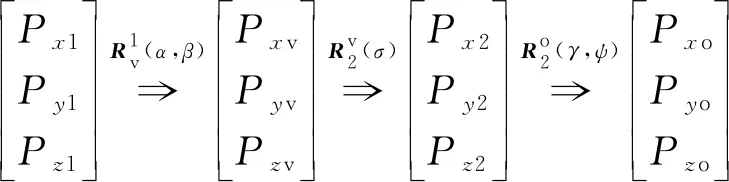
(9)
在巡航导弹制导飞行过程中,需要对导弹速度方向和大小同时控制推力大小{o,o,o}和过载大小{,}来完成进攻任务,其中代表弹道系下向过载,代表弹道系下向过载。具有末端攻击角度和时间约束的巡航制导需要满足末端条件如下:
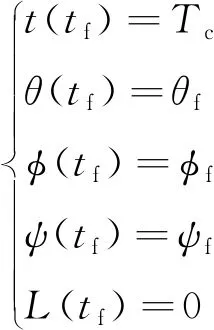
(10)
式中:为终端打击时间;为期望攻击时间。
2 攻击角度/时间约束制导律
本节基于上一节中的巡航导弹运动模型,首先基于二阶无静差系统设计等高飞行制导律,通过反馈速度误差项完成等速制导律推力指令设计;在此基础上,分别推导航向最优制导律(Heading optimal guidance law,HOGL)和航向攻击角度约束最优制导律(Heading impact angle optimal guidance law,HIAOGL),设计了一种指数型附加航向误差项,并通过末端约束条件完成附加项增益系数的在线求解,实现两种不依赖于剩余时间精确估计的时间约束制导律设计。所提出的攻击角度/时间约束制导律设计架构如图2所示。
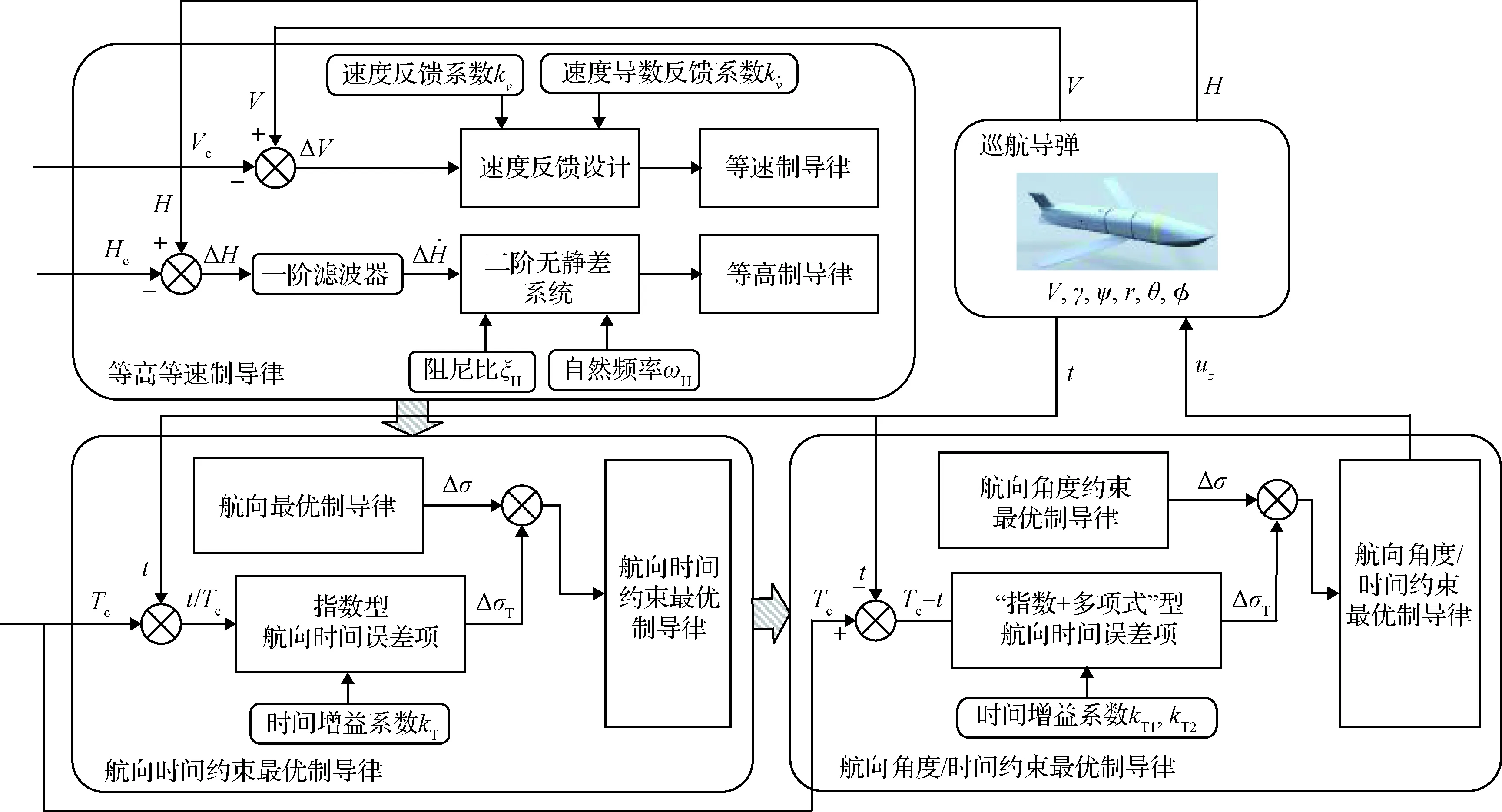
图2 巡航导弹攻击角度/时间约束制导律设计架构
2.1 等高等速制导律
巡航导弹在执行进攻作战任务过程中,需要维持一定的飞行速度和较低飞行高度以躲避舰船雷达探测系统以接近目标,进而完成对目标的打击任务,本节开展等高等速制导律的设计。
巡航导弹飞行高度需要满足如下条件:
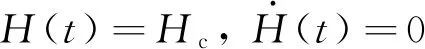
(11)
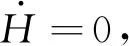
Δ=()-
(12)
对式(1)中第四式求导可得:
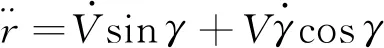
(13)
由于地心距可表示为:
=+
(14)
将式(14)代入式(13)可得:
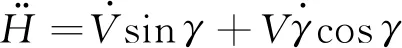
(15)
对式(12)求二阶导并将式(15)代入可得:
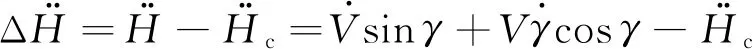
(16)
对式(1)中的第二式进行改写:
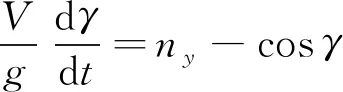
(17)
将式(17)代入式(16)可得:
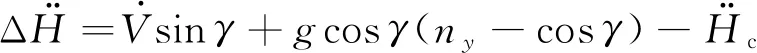
(18)
考虑巡航导弹在飞行过程中具有二阶动力学特性,因此可将高度控制回路转化为经典控制理论中的二阶无静差系统,可得到如下高度特性关系式:
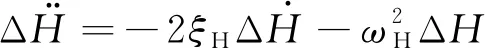
(19)
式中:表示高度特性阻尼比;表示高度特性自然频率。将式(16)代入式(19)可得高度控制指令:
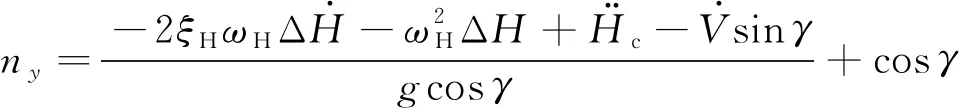
(20)
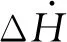
对于等速巡航飞行需要满足如下条件:
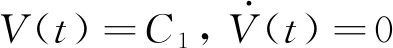
(21)
式中:为巡航导弹的巡航速度大小。巡航导弹对于速度大小的控制需要根据导弹的实际飞行状态和发动机推力大小来控制,由式(1)中第一式可知推力在体坐标系下的表达式如下所示:
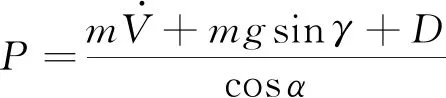
(22)
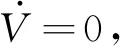
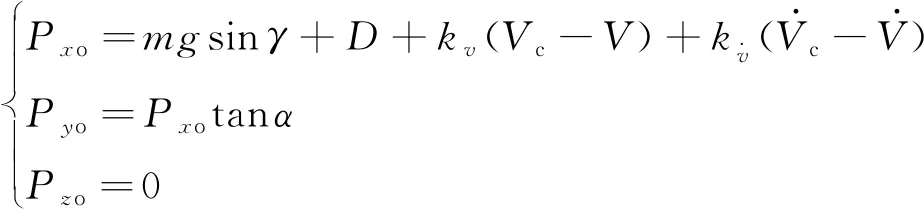
(23)
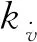
2.2 攻击角度/时间约束制导律建模
对式(6)中的第二式求导可得:
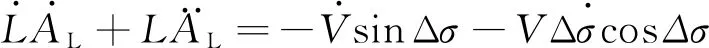
(24)
将式(5)和(6)代入式(24)中可得:
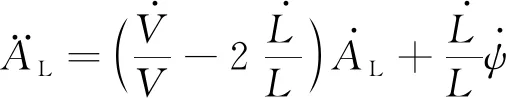
(25)
针对末端约束仅为位置约束而无角度约束问题,可基于最优控制原理求解式(25)得到HOGL为:
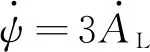
(26)
针对航向平面内末端攻击角度约束问题,选取末端航向角之差和航向视线角速率作为状态变量:
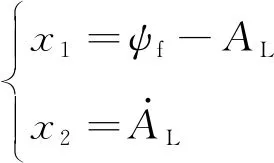
(27)
结合式(25)和(27),可得航向平面运动内状态方程如下:
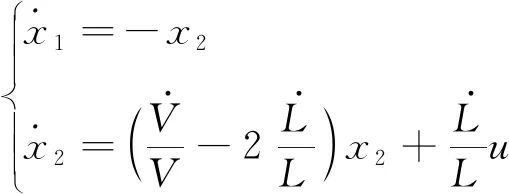
(28)
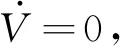
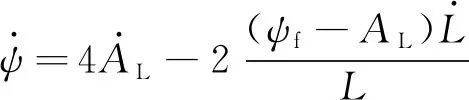
(29)
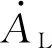
2.3 攻击时间约束制导律
为保证在制导律末端能够按照期望攻击时间打击目标,需要满足以下条件:
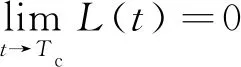
(30)
制导律式(26)以能量消耗最小作为性能指标完成航向误差的消除。因此,为了控制打击时间,设计能够令巡航导弹能在航向产生自适应机动的附加航向误差项Δ,并将其附加到制导律式(26)中,本文设计附加航向误差如下:

(31)
式中:为时间增益系数,满足>0。其中仅包含当前飞行时间,进而完成不依赖剩余时间估计的附加航向误差项设计。
由式(31)可知,随着时间增益系数的增加,巡航导弹航向机动轨迹增大;巡航导弹接近目标的过程中,飞行时间将满足→,此时随着附加航向误差减小,最优制导律将占据主导,因此所设计制导律既保证了打击时间约束又满足了制导精度要求。将式(31)代入式(6)中第一式可得:
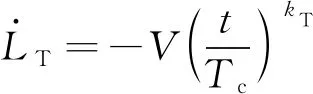
(32)
式中:为附加射程,通过调整附加射程来满足期望打击时间。将式(32)从当前时刻积分到期望打击时刻可得:
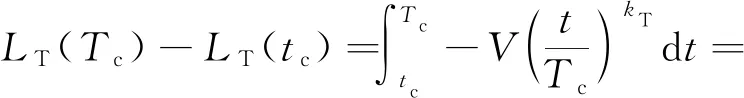
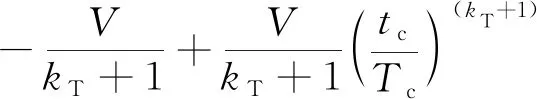
(33)
为保证在制导律末端满足()=0,由式(33)可得关于时间增益系数的表达式如下:
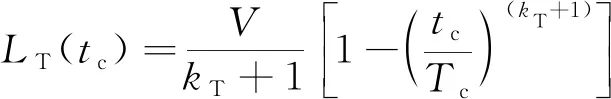
(34)
由式(34)可得,时间增益系数与导弹速度、期望打击时间和附加射程相关,由于在求解过程中附加射程()无法计算,因此对附加射程进行重构,实现对的求解。可构造如下函数:
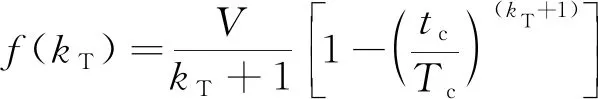
(35)
对式(35)进行求导可得:
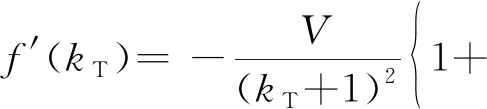
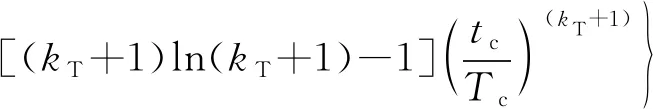
(36)
令()=(+1)ln(+1)-1,求导可得:
′()=ln(+1)+1
(37)
由式(37)可知()为单调递增函数,其最小值(0)=-1,同样可构造如下函数:
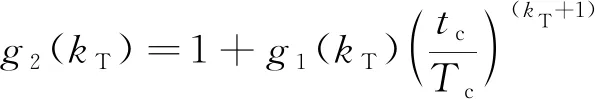
(38)
对式(38)求导可得:
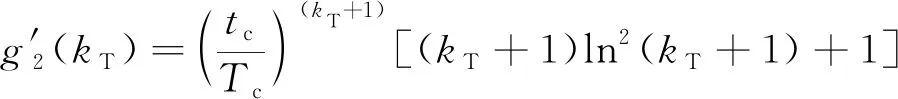
(39)
在>0条件下′()>0恒成立,因此可得到()=(0)=1->0,将其代入式(36)可知′()<0恒成立,由此可知式(35)是单调递减函数,可得到如下极值参数:
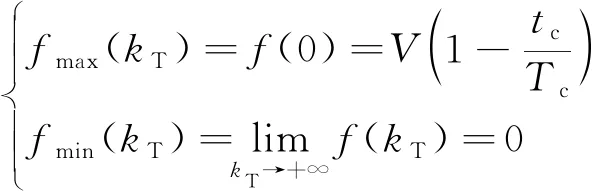
(40)
根据式(40)可对剩余射程重构如下所示:
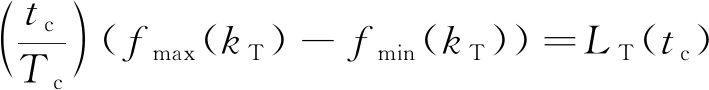
(41)
由式(41)可知,随着→满足→0;结合式(31)可知,随着飞行时间接近期望时间,附加航向误差Δ趋向于零。将式(41)代入式(34)可得:
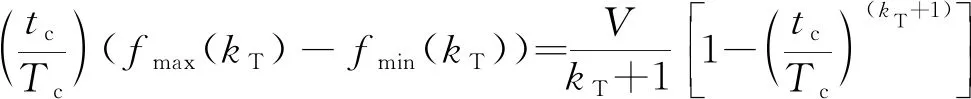
(42)
可通过数值方法求解式(42)得到,实现附加航向误差的设计。
综上,将附加航向误差Δ代入原最优制导律式(26)中,并结合式(6)中第二式得到一种不依赖剩余时间估计的航向攻击时间最优制导律(Heading impact time optimal guidance law,HITOGL)。
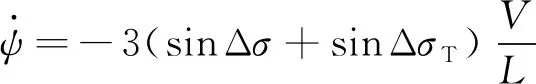
(43)
式中:-3sin Δ为航向误差控制项,保证末端航向打击精度;-3sin Δ为攻击时间控制项,保证攻击时间满足约束。本制导律通过设计具有快速收敛特性的附加航向误差Δ,基于末端约束在线求解最优时间增益系数,完成HITOGL制导律设计。
2.4 攻击角度/时间约束制导律
为同时实现末端角度和时间约束,本节在航向攻击角度约束最优制导律(HIAOGL)基础上设计附加航向误差,来保证攻击时间约束。
将式(6)中第二式除以第一式可得:
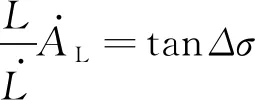
(44)
结合式(44)和式(6)中的第一式可重新构建航向相对运动方程如下:
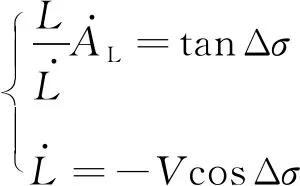
(45)
式(45)为复杂非线性运动方程,直接用附加航向误差来实现打击时间约束是难以完成的。因此在Δ为小角度情况下进行泰勒展开可得:
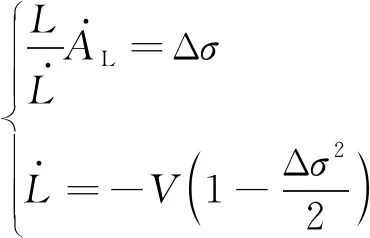
(46)
具有攻击角度/时间约束的巡航制导律需要满足的末端条件如下:
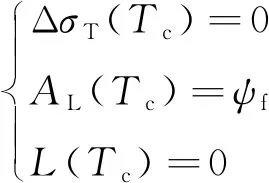
(47)
式中:第一式表示采用航向制导律机动后,附加航向误差Δ最终在=时刻收敛到零;第二式表示在=时刻末端航向攻击角度趋近于;第三式表示在=时刻导弹对目标可以满足精确打击要求。为满足以上约束,可设计附加航向误差Δ如下:
Δ=(-)(1-e-(-))
(48)
由式(48)可知,在期望攻击时刻满足约束Δ()=0,保证了原制导律的收敛性。且通过采取(1-e-(-))项的设计可以保证在剩余射程较大时,附加航向角可以快速收敛;在剩余射程较小时产生的航向机动误差较小,不影响HIAOGL制导律的收敛精度。因此不依赖剩余时间估计的攻击角度/时间约束制导律设计转化为参数和的求解,将式(48)代入式(46)的第一式可得:
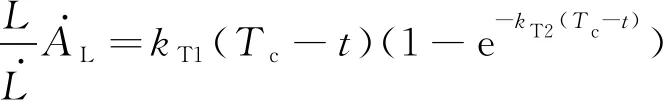
(49)
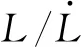
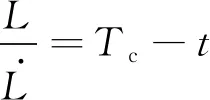
(50)
因此式(49)化简为:
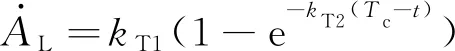
(51)
对式(51)从当前时刻积分到期望攻击时刻可得:
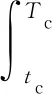
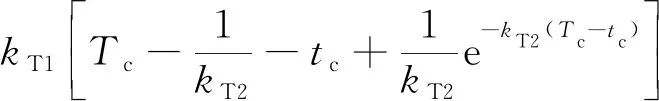
(52)
结合式(47)中的第二式末端航向攻击角度约束,式(52)可改写为:
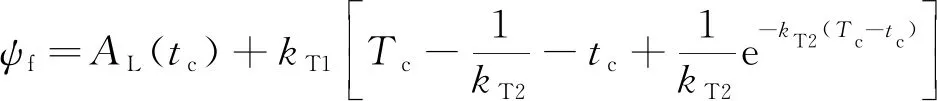
(53)
将航向机动误差式(48)代入式(46)中第二式可得:
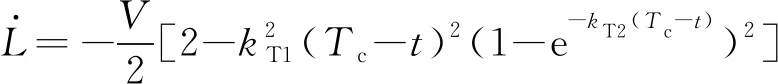
(54)
将式(54)从当前时刻积分到期望打击时刻可得:
()-()=
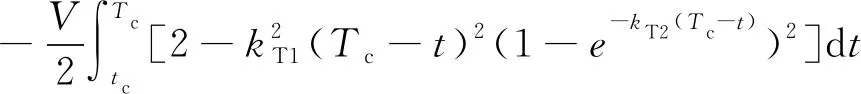
(55)
结合式(47)中的第三式末端位置约束求解可得:
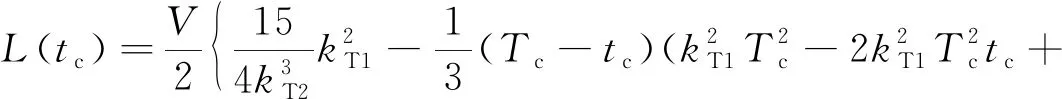
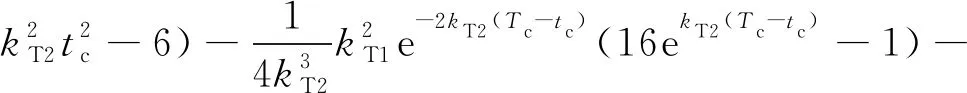
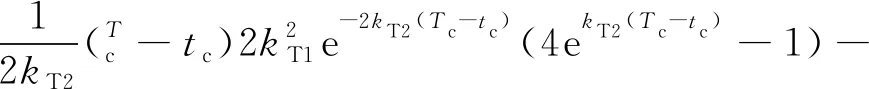
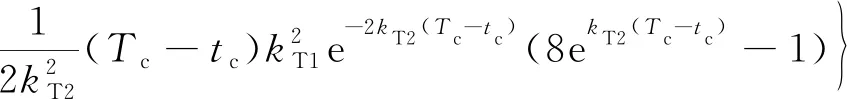
(56)
结合式(53)和(56)为一个代数方程组,此方程组只包含两个时间增益系数和,因此可采用数值方法求解。将式(48)附加到HIAOGL中,可得到一种不依赖剩余时间估计的航向角度/时间最优制导律(HITAOGL):
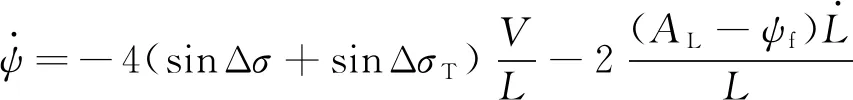
(57)
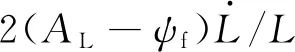
弹道系下向过载如下:
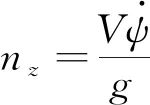
(58)
因此,将式(43)和式(57)代入到式(58)中便可实现所需约束条件的制导飞行。本文所提出的不依赖剩余时间估计的制导律,有效解决了现有制导律对于剩余时间精确估计的强依赖性的问题,极大地提高了角度/时间约束制导律在工程中的应用。
3 制导律收敛性分析
本节通过求解常规航向偏置导引律的闭环解,HITOGL和HITAOGL两制导律的收敛特性,得到制导律收敛条件。
由文献[21]可得常规航向偏置导引律形式如下:
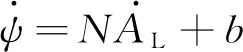
(59)
对式(5)进行求导,并将式(6)和式(59)代入可得:
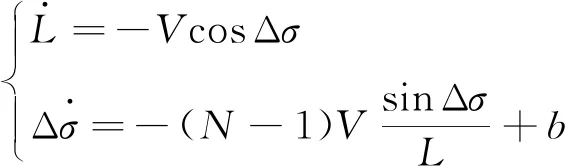
(60)
令d=||d,对偏置项进行归一化处理如下:
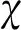
(61)
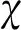
将式(61)代入式(60)可得:
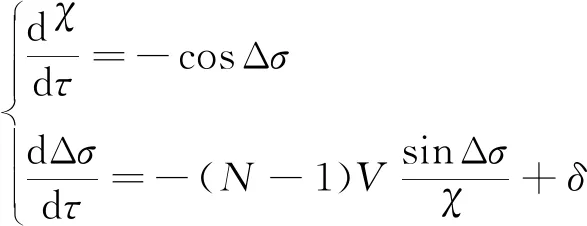
(62)
式中:符号变量表示偏置项的符号,所以=±1为常值。
将式(62)两方程相除可得:
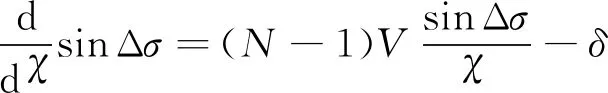
(63)
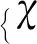
当≠2时,求解方程(63)可得:
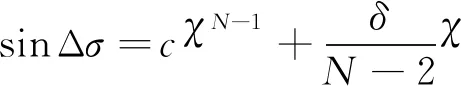
(64)
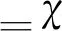
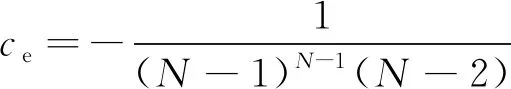
(65)
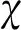
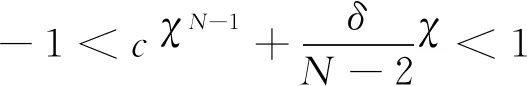
(66)
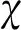
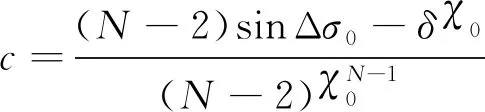
(67)
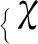
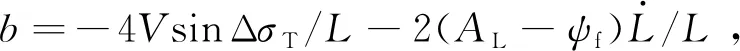
当=1时,为满足轨迹收敛需要满足<且Δ<π2,求解式(67)可得:
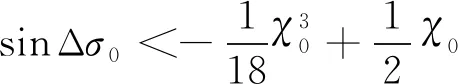
(68)
当=-1时,为满足轨迹收敛需要满足>且Δ>-π2,求解式(67)可得:
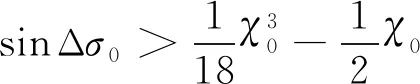
(69)
由此,通过根据初始条件判断不等式(68)或式(69)是否成立判断弹道轨迹收敛情况。由此得到满足HITOGL和HITAOGL轨迹收敛的仿真初始条件,为本文设计的制导律在工程中实际应用提供了参考。
4 仿真分析
4.1 不依赖精确剩余时间制导律验证
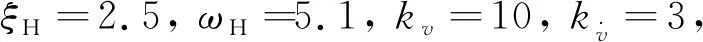

表1 仿真场景设定

表2 仿真约束条件
采用上文中设计的HITOGL和HITAOGL两种制导律进行仿真分析,仿真结果如图3~图5所示:

图3 速度与高度变化曲线

图4 推力和航向过载变化曲线

图5 航向角和飞行轨迹变化曲线
由图3可知,HITOGL和HITAOGL在采用等高等速制导律飞行速度在85 s之后收敛稳定且速度误差均在0.01 m/s以内;飞行高度在3.8 s之后均收敛稳定,且高度误差均在0.1 m以内。由图4(a)可知,在等高等速制导律作用下,在初始阶段需要增加推力来实现速度和高度趋于期望值,在等高等速飞行阶段,推力大小稳定;由图4(b)可知,采用HITOGL和HITAOGL航向过载均在1以内。
4.2 不依赖剩余时间估计制导律算法适应性分析
通过改变期望攻击时间和攻击角度约束,验证HITAOGL对不同作战任务的适应性。
不同期望攻击时间的仿真结果如图6和表3所示,其中攻击角度误差均在0.2°以内,实际攻击时间误差均在0.1 s以内,随着期望攻击时间的增加,导弹的位置误差也随之增加。
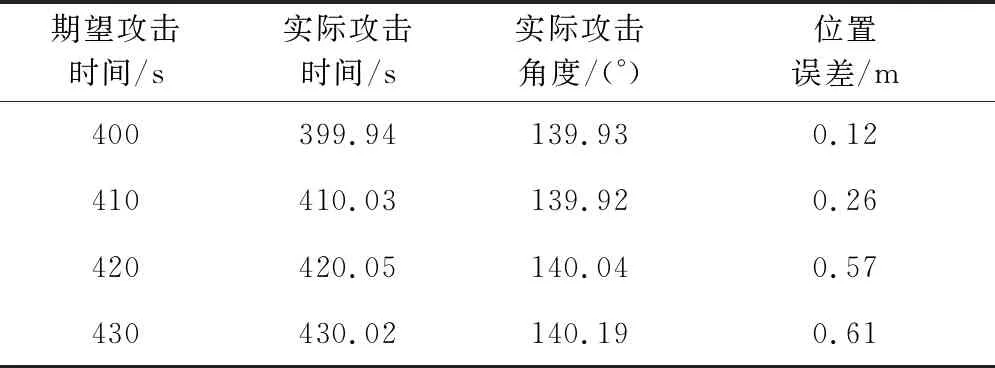
表3 不同期望攻击时间条件下打击结果

图6 不同期望攻击时间条件下航向角和飞行轨迹曲线
同样,不同攻击角度约束的仿真结果如图7和表4所示,其中攻击角度误差均在1°以内,时间误差均小于0.2 s,位置误差均小于1 m,随着攻击角度约束和初始航向角之差增大,实际攻击角度误差和实际攻击时间误差也逐渐增大。
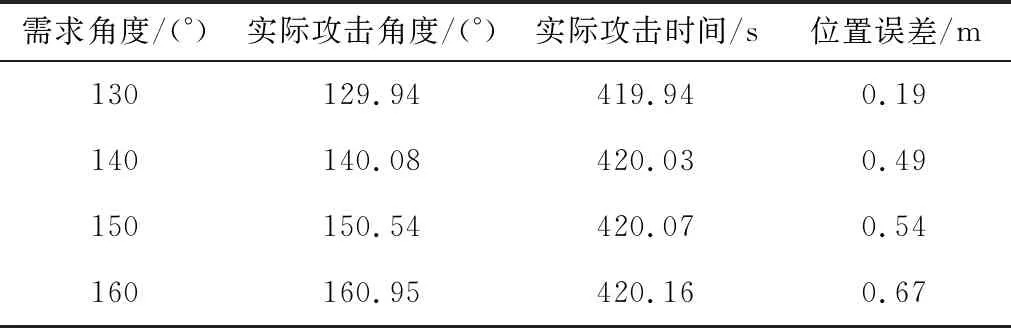
表4 不同期望攻击角度条件下打击结果
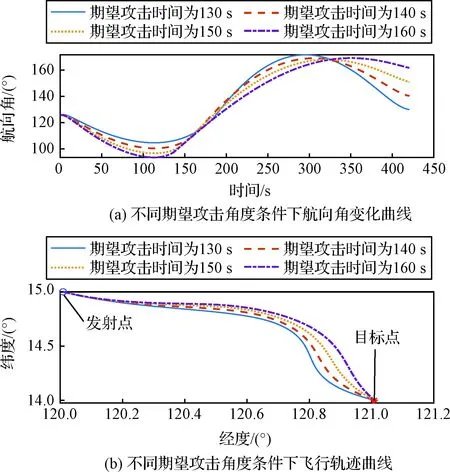
图7 不同期望攻击角度条件下航向角和飞行轨迹曲线
经过200次蒙特卡洛打靶仿真得到平均脱靶量为0.64 m,终端攻击角度误差平均值为0.41°,攻击时间误差平均值为0.13 s,说明本文设计的制导律在干扰因素的影响下具有良好的鲁棒性。
最后,为验证HITAOGL的鲁棒性,设置服从均匀分布的干扰因素(见表5)并进行200次蒙特卡洛打靶仿真,结果见表6。

表5 干扰因素列表
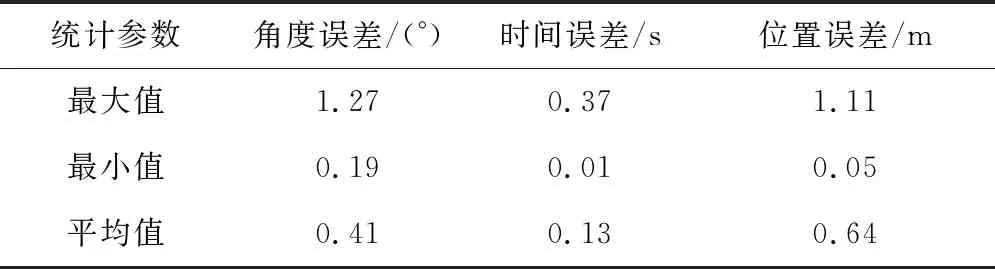
表6 打靶结果
5 结 论
本文针对巡航导弹末端多约束制导问题,设计了一种不依赖剩余时间估计的制导律,实现了末端航向攻击角度/时间约束精确制导飞行。首先,通过对航向弹目相对运动关系进行重构,将附加航向误差项附加到HOGL中得到满足攻击时间约束的HITOGL;在此基础上,通过将角度约束制导律与时间约束制导律相结合,设计不依赖剩余时间约束附加项,通过在线求解时间增益系数实现轨迹的自适应在线机动,进而实现HITAOGL的设计。通过求解通用偏置导引律闭环轨迹,给出满足HITAOGL的显式收敛初始条件。最后通过数学仿真验证了本文设计的制导律的有效性、收敛性和鲁棒性,经过200次蒙特卡洛打靶仿真得到平均攻击角度误差为0.41°,平均时间误差为0.13 s。

