面向火箭构型论证的运载能力快速分析方法

刁 尹，王永海，卢宝刚，韦常柱

(1. 哈尔滨工业大学航天学院，哈尔滨 150001；2. 北京临近空间飞行器系统工程研究所，北京 100076；3. 北京航天长征飞行器研究所，北京 100076)

0 引 言

作为衡量火箭性能最直接也是最重要的指标，运载能力可为火箭总体参数快速论证与任务规划提供重要的参考依据，特别是在构型论证与任务规划阶段，运载能力估值过高可能会造成代价高昂的减重甚至导致运载任务失败；相反，估值过低则会浪费宝贵的运载能力。然而，由于受到火箭总体参数、任务模式和计算条件等多方面的限制，难以找到具有一定通用性的火箭运载能力快速计算方法，特别是在型号论证初期，需要一种能够满足不同构型和任务条件下运载能力快速计算的普适方法。

针对火箭运载能力计算问题，目前主要有离线弹道积分、在线制导和纯工程经验估算等方法。离线弹道积分方法通过将问题转化为多约束参数优化问题对运载能力进行离线积分计算，需要进行精细化建模且计算效率较低；在线制导方法通常基于自适应伪谱法、间接法、凸优化和改进迭代制导等原理，通过设计与火箭实时状态和目标任务精确匹配的制导模型完成剩余运载能力的求解，在总体论证和构型优化阶段，制导系统的反复更改会导致求解模型的复杂化，且具有统一形式的凸优化和联立法等方法也存在非凸约束转化、收敛性和计算效率等问题；纯工程经验估算方法主要通过对以往型号任务与飞行经验的总结，对包括有效载荷在内的各部分质量参数进行粗略估计，构型论证阶段缺乏可用于参照的模型数据，且计算精度较低。

因此，上述方法均无法同时满足火箭总体构型与任务的快速论证中的准确性、快速性和普适性要求。而运载能力求解问题可以转化为具有普适性的最大载荷条件下的速度损失计算问题，但目前仅有对火星滑行段气动阻力速度损失的研究成果。

针对不同构型与任务条件下的运载能力快速计算问题，本文研究了基于高斯函数与组合神经网络的火箭运载能力快速计算方法。首先，将运载能力转化为速度损失项求解问题，并给出方法整体框架；其次，在状态量解析计算分析的基础上，采用高斯函数对核心的重力速度损失项进行拟合计算；为提高样本的采样密度，简化数据建模过程，并增强针对不同构型与任务的适应性，采用RBF+DNN组合网络进行重力速度损失回归分析；然后，考虑发射条件和任务参数，给出了运载能力快速迭代求解方法；最后，通过仿真实验验证了方法的有效性，并给出本文结论。

1 运载能力评估方法

1.1 整体框架

在给定构型基本总体参数和初始任务条件下，通过实际速度增量与等效需要速度之间的匹配关系判断任务的可达性，并通过调整任务参数完成运载能力的迭代求解。其中，实际速度增量计算的关键在于速度损失项；而重力速度损失作为速度损失项中占比最大和快速准确求解难度最高的部分，是本文研究的核心。为此，构建了不同构型与任务条件下的数据样本，并分别采用基于状态量解析特性分析的高斯函数与RBF+DNN组合神经网络进行重力速度损失相关的样本训练与模型调用。本文所研究方法的整体框图如图1所示。

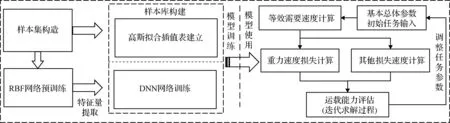
图1 整体框图

1.2 速度损失估计

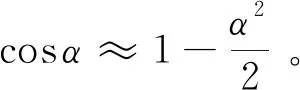
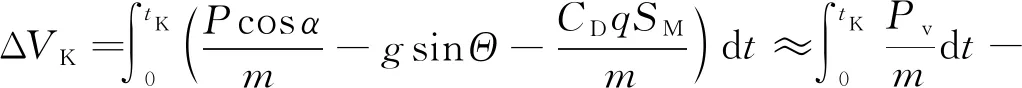
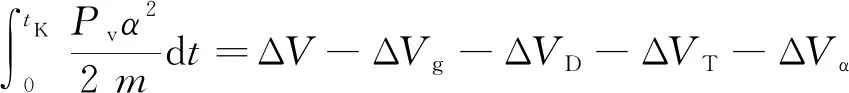
(1)

式中：Δ为理想速度增量；Δ为重力速度损失；Δ为气动阻力速度损失；Δ为喷口压力速度损失；Δ为攻角速度损失；为关机时间；与分别代表实际推力与真空推力；为质量；为重力加速度；为当地弹道倾角；为气动阻力系数；为动压；为发动机喷口面积；为箭体气动参考面积。

运载火箭二级及以上飞行阶段大气稀薄，由气动阻力和喷口压力产生的速度损失可忽略不计。此外，不同火箭构型与任务条件下最大气动阻力系数所对应的高度和马赫数接近，可采用同一拟合系数进行计算。根据运载火箭总体设计经验，气动阻力速度损失和喷口压力速度损失可写成：

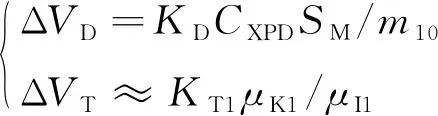
(2)

式中：为气动阻力损失系数，可根据最大气动阻力系数对应的高度和马赫数查表得到；为一级起飞质量；为一级压力损失系数，可取为与火箭构型相关的常量；和分别为火箭一级关机点的质量比和比冲比。

在速度损失组成中，气动阻力速度损失和喷口压力速度损失占比很小；由二次攻角引起的攻角速度损失通常可以忽略；重力损失项作为火箭速度损失的主要组成部分，是运载能力计算的关键环节。

2 重力速度损失的高斯拟合方法

2.1 分段处理

重力速度损失主要与重力加速度和发射坐标系下的当地弹道倾角有关，而重力加速度是地心距的函数，可采用拟合函数对地心距和当地弹道倾角进行回归分析，进而完成对重力速度损失的计算。根据运载火箭飞行特点，按照垂直飞行段、一级飞行段(不含垂直飞行段)和二级及以上飞行段进行重力速度损失估算研究。

(1)垂直飞行段

火箭垂直飞行时间较短，重力加速度可认为不变，当地弹道倾角基本保持为90°，因此垂直飞行段重力速度损失为：

Δ=

(3)

式中：为运载火箭地面重力加速度；为运载火箭垂直飞行时间，可根据起飞推重比进行计算。

(2)一级飞行段(不含垂直飞行段)

根据总体设计经验，运载火箭一级重力速度损失可采用如下公式进行准确估算：

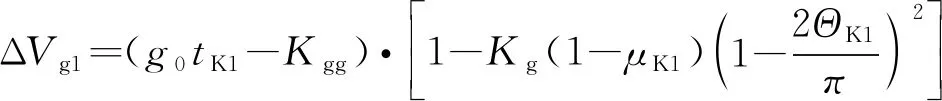
(4)

式中：为减去后的一级飞行时间；为一级关机点当地弹道倾角；为引力场修正系数；为转弯修正系数。上述两个系数可通过已有工程数据查表得到。

由式(4)可知，为准确计算一级飞行段重力速度损失，需要精确求解，而与任务类型、轨道高度及飞行时间等因素密切相关，可将一级关机点以后飞行段的和地心距拟合成随时间变化且与任务相关的函数，然后根据任务类型、轨道高度和一级工作时间得到。

(3)二级及以上飞行段

在完成，随时间变化曲线拟合后，可由准确得到重力加速度的值，则二级及以上飞行段的重力速度损失可通过简单积分快速获得。

2.2 状态量解析解分析

为选择合适的方法对与进行拟合计算，进行状态量解析计算研究。当运载火箭处于一级关机点以后飞行阶段时，可忽略气动力，运载火箭在射面内飞行，且最优飞行攻角接近于0，可得到简化的动力学方程：

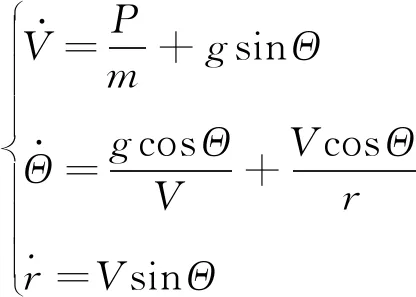
(5)

式中：为发射系速度大小。

为了便于积分，令=sin，则有：

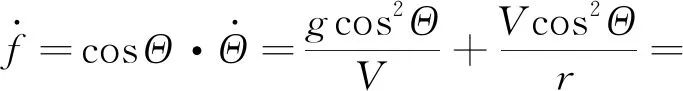
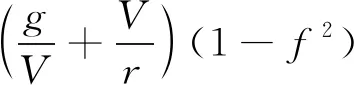
(6)

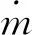
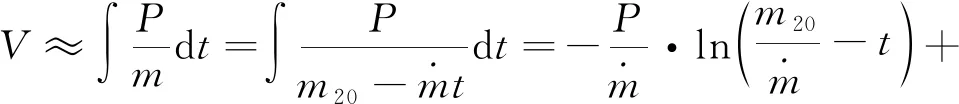
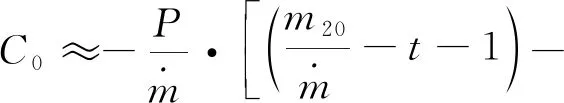
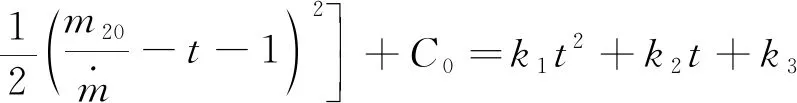
(7)

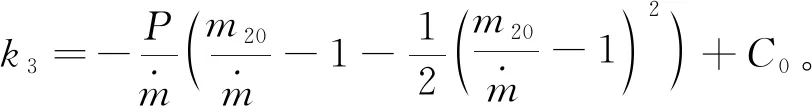
进而可得到的解析形式：

(8)

式中：为积分常数。

2.3 高斯拟合方法

由于实际速度变化更加复杂，上述直接求解形式耗费过大，可将其等效简化为经典的高斯函数形式，利用高斯函数对=sin进行准确拟合：

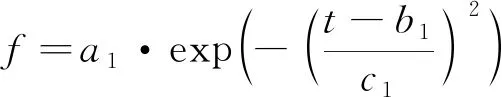
(9)

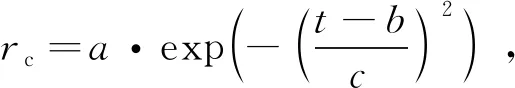
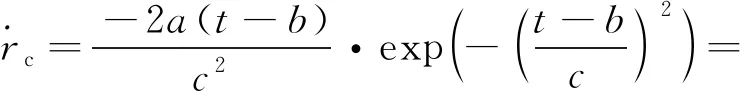
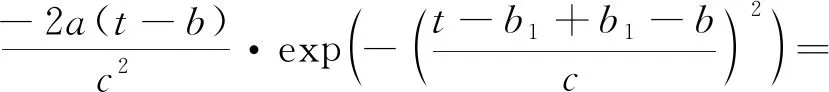
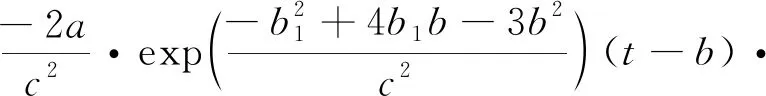
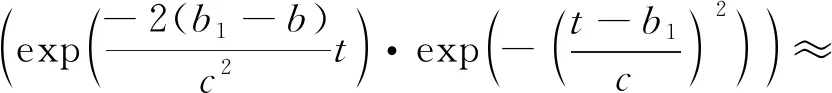
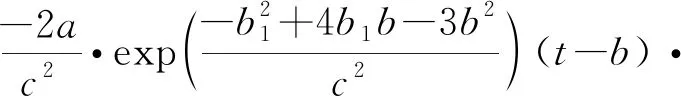
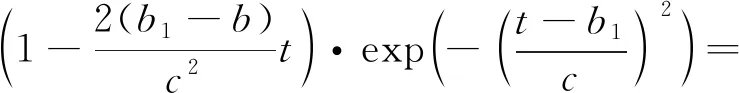
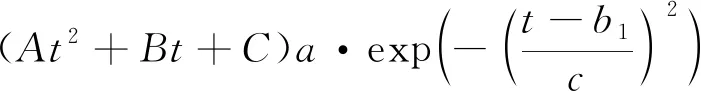
(10)

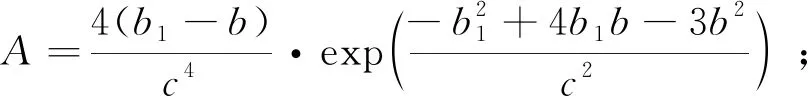
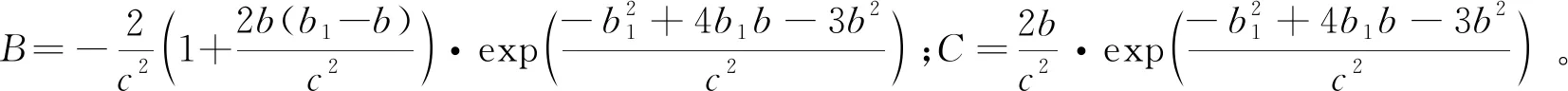
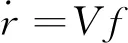
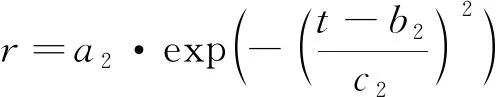
(11)

式中：,,为高斯拟合系数，可通过弹道样本拟合求得。为了精确计算高斯拟合系数，需要在不同构型与任务条件下进行弹道精确设计，得到能够覆盖多构型多任务的高斯拟合系数表。

此外，为消除由当前构型飞行总时间与拟合所用标准总时间不一致带来的拟合误差，可根据比例关系得到修正后的拟合时间：

(12)

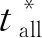
重力速度损失计算流程如图2所示。

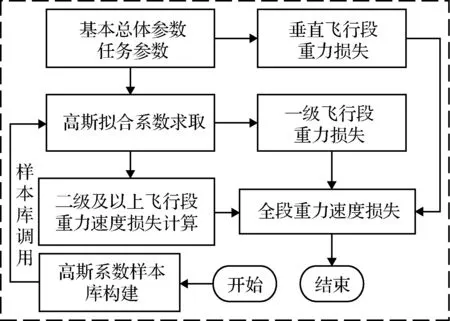
图2 重力速度损失计算流程

3 重力速度损失的组合神经网络拟合方法

本文采用RBF+DNN组合神经网络优化重力速度损失的计算过程。组合神经网络能够批量地处理不同构型与任务的样本数据，增强了对不同构型与任务的适应性；并且同一条飞行轨迹上按照一定间隔取的不同状态点均可作为样本数据，提高了样本的采样密度；同时省去了高斯拟合系数插值表的构建过程。模型训练时采用以收敛速度和结构复杂度为指标择优选出的状态特征量序列作为输入，并以对应样本的重力速度损失序列作为输出；模型使用时以任务要求的状态特征量(=1,2,…,)作为输入，估算重力速度损失Δ。

(1)组合神经网络结构

RBF具有单隐含层的简单结构和收敛速度快的特性，输入输出节点数与数据输入输出维数一致，隐含层节点数与权值系数可根据OLS算法求得，而且可以证明：正则化的RBF网络针对任意未知非线性函数，总存在一组最优逼近网络权值系数。因此在模型预训练时，先采用收敛性较好的RBF网络对输入状态特征量进行选择性提取；进而利用DNN对重力速度损失进行精确拟合训练。

(2)网络训练与使用

为防止欠拟合与过拟合等问题，在对数据进行归一化处理的基础上，采用留出法划分样本，训练、验证和测试样本数量占比分别为75%, 15%和15%；然后采用隐含层节点数自动生成策略进行网络结构训练，即根据训练误差下降速度和实时网络验证误差大小决定是否需要增加新的隐含层节点，保证训练误差按照指定的速度收敛至给定阈值。

根据运载火箭总体参数、任务参数以及训练收敛的网络模型即可快速得到重力速度损失。

图3 组合神经网络的结构关系

4 运载能力快速迭代求解方法

利用构建好的高斯系数库或神经网络模型对火箭运载能力进行快速计算的流程如图4所示。

图4 运载能力计算流程

5 仿真校验

本文首先采用3种不同的常见火箭构型建立通用样本数据库，生成高斯拟合系数插值表并完成神经网络训练，然后以H-2A运载火箭为测试样例，计算火箭各项损失速度，进而完成运载能力计算，并与优化结果进行对比，评估方法的有效性。

(1)样本集构建

样本库构建是保证模型具有普适性的关键。本文选用两级、两级半和三级等3种构型的运载火箭进行样本库构建，各构型主要总体参数见表1。

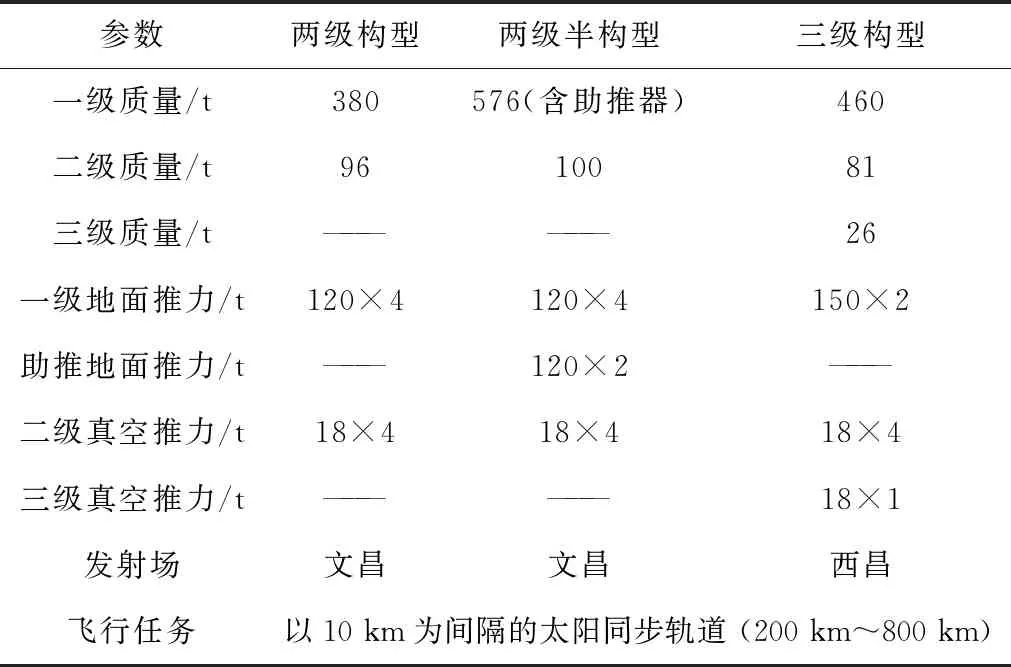
表1 不同构型运载火箭总体参数

分别设计了不同发射条件、有效载荷和任务参数的195条飞行弹道，在每条飞行弹道中，按照一定时间间隔扩张存取样本点，构建得到了包含259740条数据的样本库，其中3种不同构型样本库分别包含71903条、106834条和81003条样本。

(2)高斯拟合系数表构建

以平均确定系数高于0.99为指标，则阶次为1的高斯拟合函数形式即可完成数据精确拟合。将飞行时间相近的不同轨道任务高度的高斯系数取均值，得到高斯系数插值表见表2。

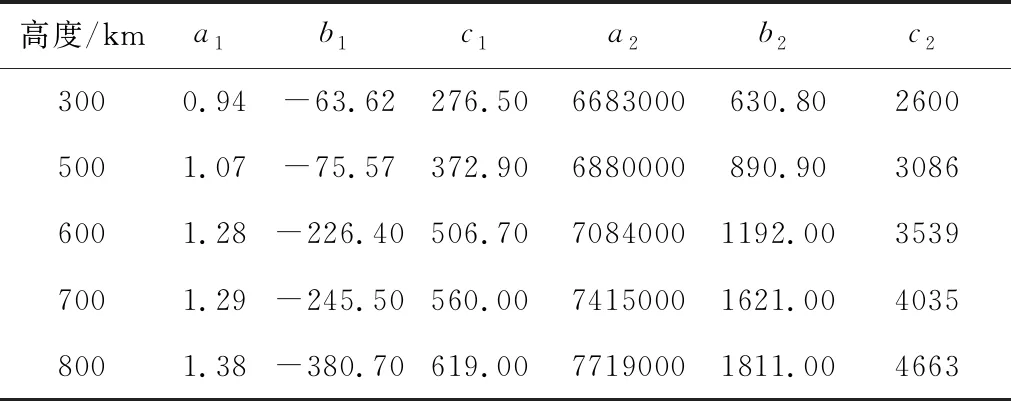
表2 高斯拟合系数

上述结果表明：6个高斯拟合系数沿轨道高度具有明确的单调特性，可以通过任务插值求取。

(3)重力速度损失神经网络模型构建

1)RBF状态特征量提取

以不同的状态特征量组合进行网络训练和测试。可用的状态特征量全集为：时间、高度、速度、重力加速度、当地弹道倾角。状态特征量备选组合包括：①时间+高度+速度+重力加速度+当地弹道倾角；②高度+速度+当地弹道倾角；③速度+重力加速度+当地弹道倾角；④高度+当地弹道倾角；⑤时间+当地弹道倾角。考虑上述不同状态特征量组合情况，分别采用RBF进行网络训练，结果见表3。

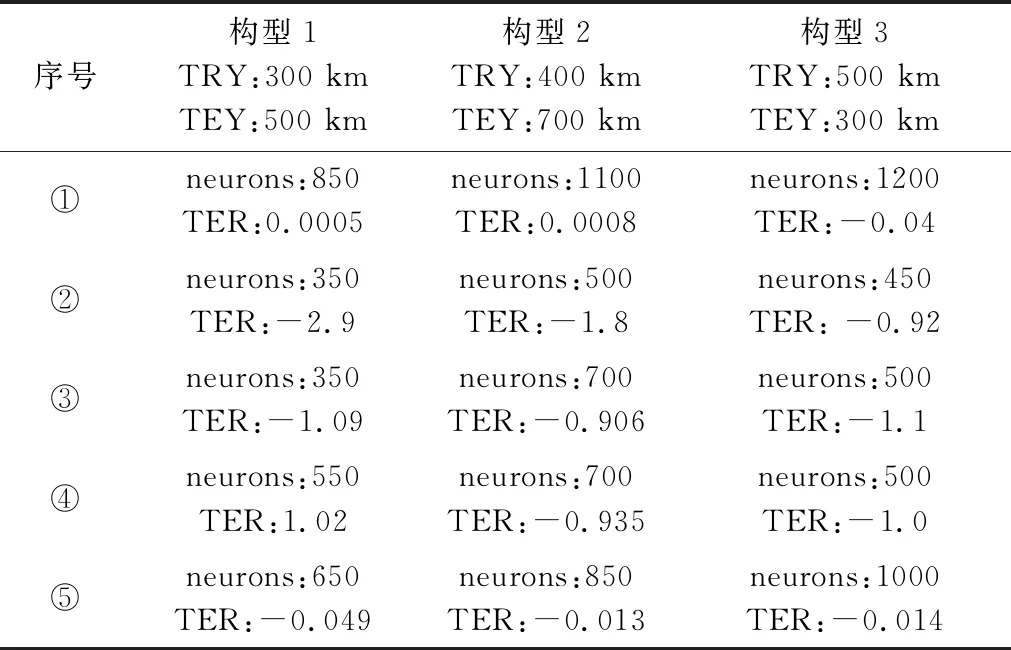
表3 不同特征组合情况网络训练结果

TRY和TEY分别表示网络训练和测试所用的任务轨道高度。neurons表示收敛至给定精度所需要的神经元数目，TER表示测试输出的速度损失估算误差平均值(m/s)。上述算例在网络训练中的均方误差均能收敛至1×10量级。

上述结果中，组合序号②所对应的网络在满足训练与测试结果精度的前提下，具有更快的收敛速度和更简单的网络结构，因此选用组合中的高度、速度和当地弹道倾角作为状态特征量。

2) DNN速度损失模型构建

利用前述3种不同构型火箭的混合弹道样本数据进行DNN网络训练。从构型1与构型3的混合样本数据中随机抽取10000条样本进行训练和验证，然后从构型2的样本数据中随机抽取1000条样本作为测试集。训练完成的DNN结构如图5所示。

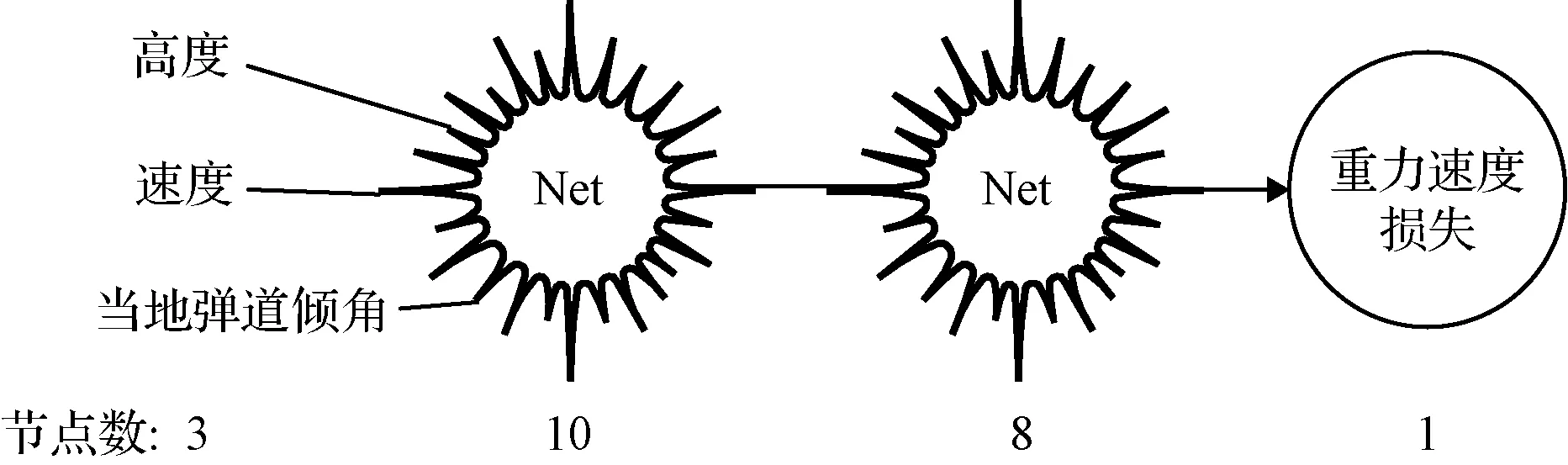
图5 DNN网络结构训练结果

网络测试结果如图6所示。

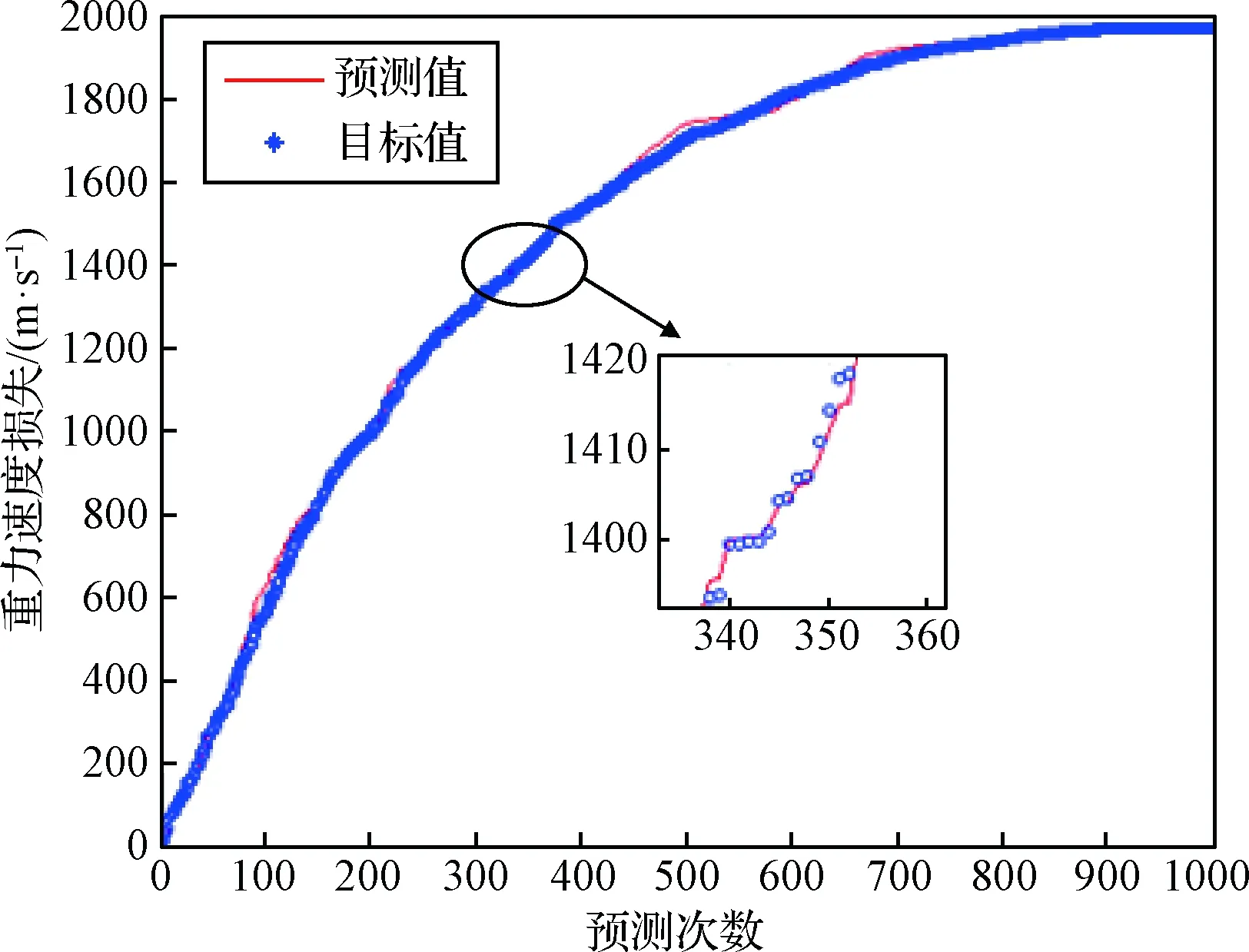
图6 DNN测试结果

由上述仿真结果可知，在1000次随机采样生成的重力损失测试样本中，测试结果中最大重力速度损失偏差为163.91 m/s，平均误差为7.20 m/s，拟合准确率高于99%。结果表明：经过特征提取后的DNN网络可对多构型与多任务条件下的重力速度损失进行有效拟合，网络测试误差小于1%，验证了方法的有效性。

(4)运载能力快速计算

前文所述3种构型仅用于样本库的拟合与训练，下文将以H-2A(2022型)两级半运载火箭为例，进行运载能力快速计算仿真校验，该型火箭的主要总体参数见表4。

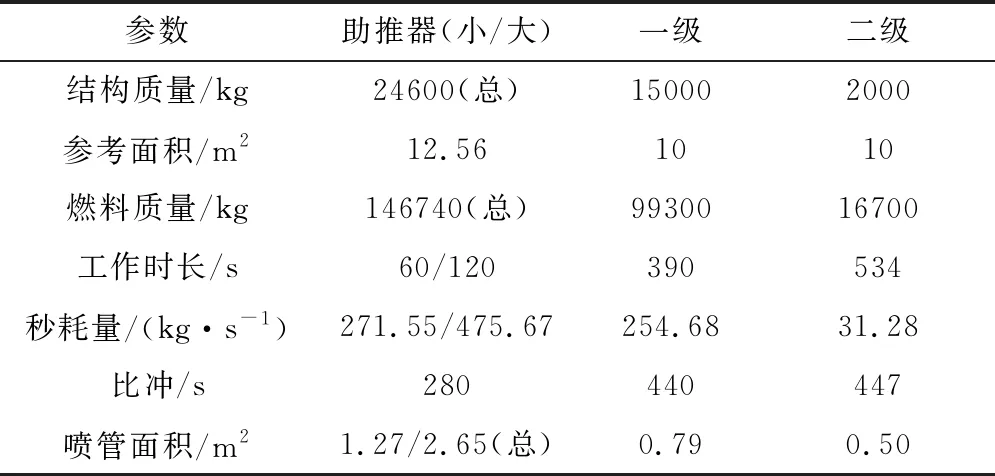
表4 H-2A运载火箭总体参数

以日本种子岛航天中心(经度131.08°，纬度31.25°，高程220 m)为发射点，设定运载任务为轨道高度500 km 的太阳同步轨道。经过粒子群数值优化仿真，得到最大运载能力为11142.00 kg。通过对优化设计的标准弹道进行积分运算，可得到精确的速度增量和各项速度损失，以此作为方法对比评价的标准值。

应用高斯拟合公式对地心距、当地弹道倾角的正弦进行精确拟合。拟合结果如图7和图8所示。

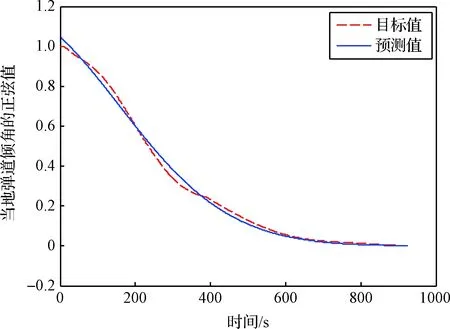
图7 当地弹道倾角的正弦值拟合结果

图8 地心距拟合结果

采用本文所提方法对速度增量与各项速度损失进行计算，结果见表5。

表5 速度增量与损失计算结果列表

上述结果表明：高斯函数和神经网络均具备对重力速度损失的准确求取能力，与标准值2522 m/s的误差均不超过2%。由于神经网络不需要进行插值表选取与积分过程，具有明显的计算速度优势，因此，后文仿真采用组合神经网络计算重力速度损失。采用本文第4部分所述的运载能力快速迭代求解方法对H-2A运载火箭的运载能力进行计算，不同轨道任务条件下的运载能力分析结果见表6。

表6 H-2A火箭运载能力

其中,为简化任务条件，除了近地点高度和远地点高度不同以外，所有任务发射场均为种子岛航天中心，轨道倾角约束均取97.38°，椭圆轨道的入轨点取为近地点，仿真计算机的配置为Intel(R)Core(TM)i5-7400。运载能力分析结果中，以500 km圆轨道任务为例：经过5次迭代计算，耗时1.63 s，得到火箭运载能力为11102.67 kg，与前文优化得到的11142.00 kg相比，运载能力估算精度误差仅为0.35%。可见本文研究的运载能力快速计算方法具有较高的准确性和任务适应性。

6 结 论

针对不同构型与任务条件下的运载能力快速计算问题，本文研究了基于高斯函数和组合神经网络的速度损失计算方法，并基于此对运载能力进行了快速分析。主要有以下结论：

(1)重力速度损失作为最大损失占比项，可采用基于状态量解析特性的高斯函数进行准确计算。重力速度损失计算误差小于2%；

(2)RBF+DNN组合神经网络具备样本采样密度高，数据建模过程简单和任务适应性强等特点，可对重力速度损失进行快速准确地计算。采用隐含层节点自适应训练的DNN只需要2个隐含层即可完成对重力损失的高精度拟合，拟合精度高于99%，耗时为毫秒级；

(3)基于速度损失计算结果，可通过一维迭代快速得到火箭运载能力。运载能力计算耗时小于2 s，计算精度偏差约为0.35%。

针对常规构型的火箭运载能力计算问题，本文所提方法具有较高的准确性、快速性和可操作性，可为运载火箭总体论证与任务规划研究提供一定参考。