一道三角填空题的多角度思考
2022-07-09 01:16江苏省启东市汇龙中学226200严晓华
中学数学研究(江西) 2022年7期
江苏省启东市汇龙中学 (226200) 严晓华
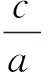
此题主要考查余弦定理、正弦定理,三角形内角和公式,熟练掌握定理是解本题的关键,属于中档题.
分析1:特殊值法,利用锐角△ABC的临界状态直角三角形这一特殊情形可求得.
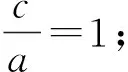
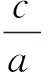
解法2:在锐角△ABC中,因为b2=a(a+c),故由余弦定理b2=a2+c2-2ac·cosB,可得a(a+c)=a2+c2-2ac·cosB,所以c2=ac+2ac·cosB,即c=a+2a·cosB,又由正弦定理,可得sinC=sinA+2sinAcosB,即sin(A+B)=sinA+2sinAcosB,得sin(B-A)=sinA,所以B-A=A,或B-A+A=π(舍去),所以B=2A,又∵A+B+C=π,所以3A+C=π,由于A,B,C均为锐角,所以
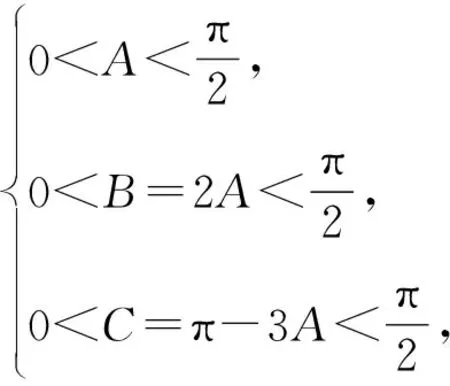
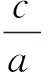
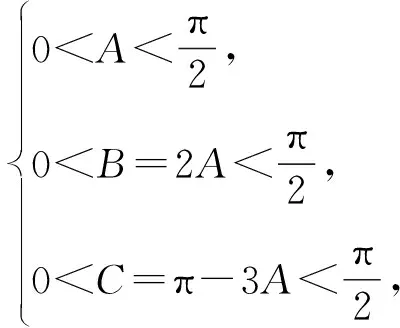

解法4:因为b2=a(a+c),所以b2-a2=ac>0,所以b>a,所以A为锐角,所以在锐角△ABC中,只需要B,C均为锐角.由余弦定理
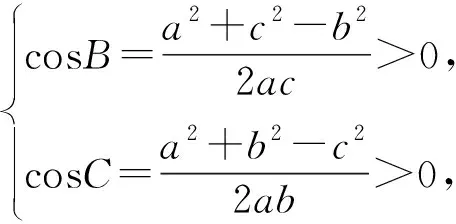
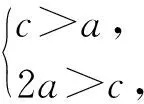
分析5:利用课本例题苏教版必修第二册P86例3:在△ABC中,当∠C为锐角时,a2+b2>c2;当∠C为钝角时,a2+b2 以上解法,各有所长,各有特色,对于学生来说,通过一题多解,可以实现对课本例题、习题的充分利用和深度发掘,锻炼学生的发散思维,培养学生应用基础知识解决具体问题的能力.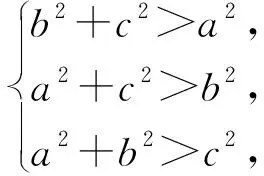
猜你喜欢
江苏安全生产(2022年8期)2022-11-01
新高考·高三数学(2022年3期)2022-04-28
中学生天地(A版)(2021年9期)2021-10-25
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14
阅读(快乐英语中年级)(2020年10期)2020-12-09
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27
创新作文(1-2年级)(2019年12期)2019-12-16
数学大王·中高年级(2019年2期)2019-01-23
智富时代(2017年4期)2017-04-27
智富时代(2017年4期)2017-04-27

