一道2022届高三调研试题的探究
2022-07-09 01:16福建省仙游华侨中学351200薛玉荣
中学数学研究(江西) 2022年7期
福建省仙游华侨中学 (351200) 薛玉荣

本题的答案是:(1)抛物线C的方程为y2=4x;(2)直线TM与抛物线C相切.第(2)问内涵丰富,不应解完即止,可进一步引导学生进行适当的探究.
1.纵向探究——一般性结论
本题(2)的结论是关于抛物线C:y2=4x,那么,对于一般的抛物线C:y2=2px(p>0),原结论是否成立?经探究,可得:





2.逆向探究——结论的逆命题
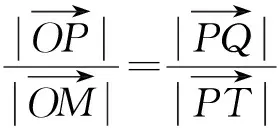




3.变式探究——新的结论
上述结论涉及抛物线C的经过顶点O的弦OM,那么,对于抛物线C的任意弦AM,会有什么相应的结论?经探究,可得:

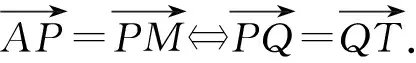
证明:下面只证明抛物线C:y2=2px(p>0)的情形.设直线AM的方程为x=hy+m,代入抛物线C的方程,并整理得y2-2phy-2pm=0.设A(x1,y1),M(x2,y2),据韦达定理得y1+y2=2ph.


进一步探究,还可以得到:


特别地,当2p=1,n=c时,结论5中关于抛物线C:x2=2py(p>0)的结论,就是2007年全国高考江苏卷题19(2)、(3)的结论:在平面直角坐标系xOy中,过y轴正方向上一点C(0,c)任作一直线,与抛物线y=x2相交于A、B两点,一条垂直于x轴的直线,分别与线段AB和直线l:y=-c交于P,Q.(1)略;(2)若P为线段AB的中点,求证QA为此抛物线的切线;(3)试问(2)的逆命题是否成立?说明理由.(图略)
以上通过对一道抛物线试题的探究,揭示了试题的深刻背景及一般规律和结论,并应用所得到的结论解决有关问题.这对培养学生发现、提出、解决问题的能力,提升学生的探究能力和数学学科核心素养无疑是有益的.
猜你喜欢
中学生数理化(高中版.高二数学)(2022年1期)2022-04-26
中学生数理化(高中版.高二数学)(2022年1期)2022-04-26
中学生数理化(高中版.高二数学)(2021年3期)2021-06-09
小学生学习指导(高年级)(2021年5期)2021-05-18
中学生数理化(高中版.高二数学)(2021年2期)2021-03-19
小学生学习指导(低年级)(2019年3期)2019-04-22
小学生学习指导(低年级)(2018年12期)2018-12-29
新高考·高二数学(2017年9期)2018-03-16
幼儿智力世界(2016年8期)2016-05-14
幼儿智力世界(2015年5期)2015-08-20

