车隧阻塞比对高铁隧道壁面气动压力特征的影响

杜建明 房倩 李建业

(北京交通大学 隧道及地下工程教育部工程研究中心，北京 100044)

高速列车从明线驶入并驶出隧道的全过程中，隧道内空气受到列车挤压会诱发一系列压力波。压力波在隧道出入口之间往复传播、反射及叠加，从而使隧道内部的瞬变压力场变得极其复杂[1]。在瞬变压力作用下，隧道壁面承受的空气压力可称其为壁面气动压力。在壁面气动压力的持续作用下，隧道支护结构内部的微裂纹会逐渐发展形成宏观裂缝，然后在动力触发作用(气动或振动效应)下发生掉块，从而给高速列车在隧道内的安全营运造成隐患。所以对高速铁路隧道壁面气动压力特征及其与影响因素之间的关系进行系统研究，对未来高铁隧道考虑气动效应作用下的结构设计，以及既有高铁隧道服役期的健康运维都有重要的科学价值与工程意义。

目前，有关高速铁路隧道壁面气动压力特征及其与影响因素关系的研究方法主要有现场实车试验[2- 3]、室内动模型试验[4- 5]以及三维数值仿真[6- 8]等。Somaschini等[3]基于大量现场实测数据对不同列车速度、隧道长度以及列车运营模式下隧道壁面气动压力峰值变化规律进行了系统总结；张雷等[5]借助室内动模型试验对高速列车经过单洞双线隧道后的壁面气动压力特征进行了研究；骆建军、刘堂红等[7- 8]利用三维数值软件分别研究了高海拔地区温度/压力与列车编组形式对隧道壁面气动压力特征的影响规律。但是，上述研究关注的焦点主要集中在列车行驶于隧道内时隧道壁面气动压力峰值及其与影响因素之间的关系。

刘峰等[9]在京沪高铁某隧道现场实车试验过程中发现，当高速列车车尾驶出隧道出口后，隧道壁面气动压力并没有即时消失，而是呈周期性衰减趋势，且气动压力持续时间更长(是列车行驶于隧道内时的11.5倍)，压力峰值可能更大(相比列车行驶于隧道内时)。随后，刘峰等[10]通过现场实车试验对高速列车车尾驶出隧道出口后，列车车速对隧道壁面气动压力特征的影响规律进行分析，发现隧道壁面气动压力峰值在列车车尾驶出隧道出口后呈指数形式衰减，而气动压力峰值随车速提高先增后减。基于现场实测数据，刘堂红等[11]通过疲劳累积损伤理论对隧道结构在气动压力作用下产生的累积损伤量进行分析，发现相比列车行驶于隧道内，列车驶出隧道后壁面气动压力对隧道结构的疲劳损伤影响是不容忽视的。无论是未来高铁隧道结构设计，还是既有高铁隧道运营维护，在充分考虑列车驶于隧道内气动压力峰值影响的同时，在列车驶出隧道后所处阶段，隧道内未消失的气动压力对支护结构的影响也不应被忽视。然而，有关高速列车驶出隧道后，隧道壁面气动压力特征及其与影响因素之间的关系研究还未引起足够重视。

随着我国大断面隧道施工技术的不断发展，隧道建造成本得到了一定程度地降低，这使得采用大断面隧道来缓解壁面气动压力对隧道结构的负面影响成为可能。有鉴于此，本研究对时速350 km的高速列车驶过长度1 000 m隧道的全过程进行三维数值仿真，然后基于仿真计算结果研究车隧阻塞比(β)对隧道壁面气动压力特征的影响规律，以期为进一步全面分析隧道壁面气动压力特征及其与影响因素之间的关系提供借鉴。

1 数值模拟计算方法

1.1 计算模型

数值模拟所用计算模型包括列车与隧道模型。列车原型为我国典型的8车编组CRH380型动车组，如图1所示。其中，头车、中间车与尾车长度分别为26.50、25.00与26.50 m，车头流线型长度为12.00 m，列车高度与宽度分别为3.70和3.38 m，车体横截面为11.22 m2。隧道原型为我国普遍采用的单洞双线高铁隧道，双线间距为5.0 m，隧道净空断面积为100.0 m2，车隧阻塞比(β)为0.112 2。当隧道净空断面积分别增大到110、120、130及140 m2时，对应车隧阻塞比分别为0.102 0、0.093 5、0.086 3及0.080 1。

当8车编组列车以时速350 km经过隧道时，根据田红旗[12]所提公式(式(1))计算可得最不利隧道长度为912.94 m，为便于后文模型构建及测点布置，隧道模型长度取1 000 m。

(1)

式中，LTU为隧道长度；Ma为马赫数；LTR为列车编组长度。

图1 数值模拟的列车模型

1.2 计算区域

数值模拟所用计算区域如图2所示。根据计算区域所处状态(是否可动)分为静止域与移动域。静止域包括隧道入口侧与出口侧计算域以及隧道域。参考既有研究成果[13- 14]，隧道入口侧与出口侧计算域尺寸均为600 m×120 m×60 m(长×宽×高)，这个尺寸可以保证计算域内的流场得到充分发展；移动域尺寸为4 400 m×5 m×5 m(长×宽×高)。

图2 数值模拟的计算区域(单位：m)

高速列车车头距隧道入口不同距离时，隧道壁面气动压力时程曲线如图3所示。由图3可见，当列车车头与隧道入口之间的距离在50～200 m之间变化时，隧道壁面气动压力时程曲线变化规律基本相似，最大正负压力峰值相差分别为2.5%和2.1%，偏差均小于5.00%。同时参考文献[8，14- 15]相关设置，数值模拟中高速列车车头与隧道入口之间的距离设定为50 m，车底与地面之间的高度设定为0.2 m。

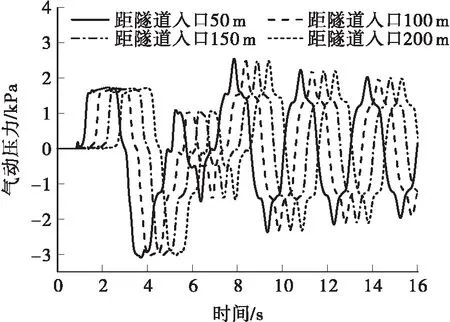
图3 列车车头距隧道入口不同距离时壁面气动压力时程曲线

1.3 边界条件

数值模拟所用边界条件如图4所示。其中，高速列车与隧道之间的相对运动通过静止域与运动域之间的接触面边界条件来实现，即滑移网格技术。有关滑移网格技术的具体设置以及实现方法参考文献[16- 17]。

图4 数值模拟的边界条件

1.4 模型网格

采用商业软件ICEM中的六面体非结构化网格对数值模拟整个计算区域进行网格划分，对列车车头/车尾以及隧道洞口网格进行局部加密，隧道与列车模型最小网格尺寸分别为0.1 m与0.004 m，模型网格如图5所示。β分别为0.112 2、0.102 0、0.093 5、0.086 3及0.080 1时，数值模型总网格单元数分别为1 679、2 015、2 375、2 740、3 148万。

图5 数值模拟的模型网格

1.5 计算参数

高速列车经过隧道诱发的流场具有鲜明的三维、可压缩、黏性以及湍流特性，对应的控制方程分别为连续性、动量以及能量方程[18- 20]。文中采用商业软件FLUENT求解器对上述控制方程进行数值求解，湍流模型采用RNGk-ε模型；隧道内压力场与速度场之间的耦合问题通过SIMPLE算法进行求解，采用二阶迎风格式对压力与动量项进行离散。所有数值计算时间步长均为0.004 s，迭代次数为50。

1.6 测点布置

隧道壁面气动压力测点布置如图6所示。其中，在隧道纵断面不同位置共布置11个监测断面，第1个到第5个监测断面与隧道入口之间的距离分别为50、100、200、300和400 m；第6个监测断面位于隧道纵向中截面，与隧道入口之间的距离为500 m；第7个到第11个监测断面与第5个到第1个监测断面对称于第6个监测断面(隧道纵向中截面)。当高速列车经过隧道后，除隧道洞口以及列车经过测点所在断面时刻表现出三维特征外，隧道壁面气动压力均呈现出显著的一维特征[21]。此外，文中研究重点主要是车隧阻塞比对隧道纵断面不同位置气动压力特征的影响规律。故在每个监测断面靠近列车一侧的隧道壁面上布置一个气动压力测点，测点与地面之间的高度为5.0 m。

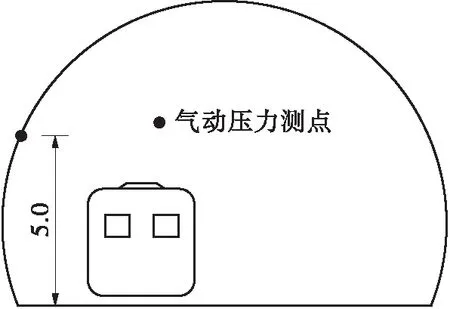
图6 隧道壁面气动压力的测点布置图(单位：m)

2 数值模拟方法验证

为了验证上述数值模拟所采用的计算区域、边界条件、模型网格以及计算参数的合理性以及准确性，将数值模拟结果与京沪高铁某隧道现场实测结果[15]进行对比。现场实测隧道净空断面积与长度分别为100.0 m2与978.0 m。现场实测所用列车为8车编组的CRH380型动车组。数值模拟采用与现场实测相同的隧道以及列车模型。隧道壁面气动压力时程曲线的数值模拟与现场实测结果对比如图7所示。其中，列车运行速度为300 km/h，隧道壁面测点与入口之间的距离为500 m。

图7 隧道壁面气动压力时程曲线的数值模拟与现场实测结果对比

由图7可见，数值模拟与现场实测的气动压力时程曲线波形变化规律基本相似，气动压力到达正负峰值的时刻基本相同。气动压力最大正、负峰值的数值模拟与现场实测结果偏差分别为3.27%与1.42%，偏差均小于5.00%，表明文中所采用的数值模拟方法能够反映高速列车过隧道的真实情况。

3 数值模拟结果分析

3.1 气动压力时程分析

为便于后文描述，将列车车头驶入隧道入口前称为阶段1；车头驶入隧道入口后，车尾驶出隧道出口前称为阶段2；车尾驶出隧道出口后称为阶段3。当高速列车处于阶段1时，列车对隧道内的空气压缩影响基本可以忽略不计，故后文主要研究阶段2及阶段3的壁面气动压力特征。隧道纵向中截面处不同车隧阻塞比下的气动压力时程曲线如图8所示。

图8 不同车隧阻塞比下隧道纵向中截面处气动压力时程曲线

由图8可见，当高速列车处于阶段2时，由于列车的存在导致隧道壁面气动压力变化无明显规律可循，主要表现为气动压力正负峰值不等；当处于阶段3时，隧道内的压力波持续在隧道出入口之间往复传播及反射，由于隧道长度与压力波传播速度在压力波传播反射过程中始终保持不变，所以隧道壁面气动压力变化表现出显著的周期性，周期T=2l/c(l为隧道长度，c为压力波传播速度)。因为压力波在隧道内传播反射过程中会受到隧道壁面摩擦、洞内空气阻力以及洞口辐射等影响，从而使得压力波所携能量逐渐被耗散，所以隧道壁面气动压力峰值表现出周期性的衰减趋势。

3.2 初始压力波时程分析

初始压力波是列车车头驶入隧道入口产生的首波，其梯度及峰值大小对出口微压波影响显著，故初始压力波时程分析对理解气动压力特征具有重要意义。隧道纵向中截面处不同车隧阻塞比下的初始压力波时程曲线如图9所示。

图9 不同车隧阻塞比下隧道纵向中截面处初始压力波时程曲线

由图9可见，对隧道纵向中截面而言，车隧阻塞比对同一截面不同位置测点的初始压力波波形变化规律影响不显著，主要影响初始压力波的梯度及正峰值。随着车隧阻塞比的增大，初始压力波梯度及正峰值逐渐增大。当车隧阻塞比从0.080 1依次增加到0.086 3、0.093 5、0.102 0以及0.112 2时，初始压力波正峰值的增加量依次为0.13、0.16、0.24以及0.30 kPa。表明随着车隧阻塞比的增大，初始压力波正峰值增加量逐渐增大。

通过对隧道壁面不同位置测点的初始压力波梯度最大值与车隧阻塞比进行拟合，发现两者之间满足以e为底的指数函数关系，相关系数R2均大于0.998，如图10所示。

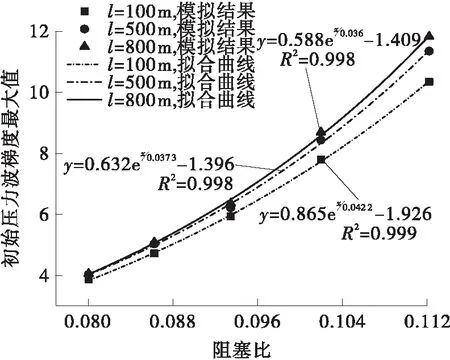
图10 初始压力波梯度最大值与车隧阻塞比的关系

由图10可见，对于隧道壁面不同位置的测点，随着车隧阻塞比的增大，初始压力波梯度最大值以指数形式增长。

通过对隧道壁面不同位置测点的初始压力波正峰值与车隧阻塞比进行拟合，发现两者之间也满足以e为底的指数函数关系，相关系数R2均大于0.999 1，如图11所示。

图11 初始压力波正峰值与车隧阻塞比的关系

3.3 阶段2的典型气动压力峰值分析

高速列车处于阶段2时隧道壁面典型气动压力峰值(正峰值、负峰值以及峰峰值)沿隧道纵向的分布曲线如图12所示。

(a)正压峰值

由图12可见，对隧道壁面气动压力正峰值而言，隧道中部显著大于隧道洞口段。对隧道壁面气动压力负峰值与峰峰值而言，当测点与隧道入口之间的距离l从50 m逐渐增加到400 m时，负峰值与峰峰值压力逐渐增大；当l从400 m逐渐增加到700 m时，负峰值与峰峰值压力逐渐减小；当l从700 m增加到900 m时，负峰值与峰峰值压力又逐渐增大；当l从900 m增加到950 m时，负峰值与峰峰值压力又逐渐减小。

随着车隧阻塞比的增大，隧道壁面纵向分布的典型气动压力峰值逐渐增大。当车隧阻塞比从0.080 1依次增大到0.086 3、0.093 5、0.102 0以及0.112 2时，以距隧道入口500 m的测点为例，隧道壁面气动压力正(负)峰值的增加量依次为0.15(0.25)、0.20(0.33)、0.27(0.43)以及0.35 kPa(0.60 kPa)。随着车隧阻塞比的增大，隧道壁面典型气动压力峰值增加量逐渐增大。

通过对隧道壁面不同位置测点的典型气动压力峰值(正峰值、负峰值以及峰峰值)与车隧阻塞比之间的关系进行拟合，发现两者之间满足以e为底的指数函数关系，相关系数R2均大于0.999 2，如图13所示。由图13可见，对于隧道壁面不同位置的测点，随着车隧阻塞比的增大，典型气动压力峰值均以指数形式增大，且隧道中截面典型气动压力峰值随车隧阻塞比的增长速率最大，隧道出口段次之，隧道入口段再次之。

(a)l=100 m

3.4 阶段3的典型气动压力峰值分析

高速列车处于阶段3时的隧道壁面典型气动压力峰值(正峰值、负峰值以及峰峰值)沿隧道纵向的分布曲线如图14所示。

(a)正压峰值

由图14可见，对隧道壁面典型气动压力峰值而言，隧道中部显著大于隧道洞口段。对隧道壁面气动压力正峰值而言，当测点与隧道入口之间的距离l从50 m逐渐增加到500 m时，正峰值压力迅速增大，并达到最大值；当l从500 m增加到700 m时，正峰值压力迅速减小；当l从700 m增加到950 m时，正峰值压力减小速率变缓。对隧道壁面气动压力负峰值而言，当测点与隧道入口之间的距离l从50 m增加到300 m时，负峰值压力缓慢增大；当l从300 m增加到500 m时，负峰值压力迅速增大，并达到最大值；当l从500 m增加到950 m时，负峰值压力迅速减小。对隧道壁面气动压力峰峰值而言，当测点与隧道入口之间的距离l从50 m增加到500 m时，峰峰值压力迅速增大，并达到最大值；当l从500 m增加到950 m时，峰峰值压力迅速减小。

通过对隧道壁面不同位置测点的典型气动压力峰值(正峰值、负峰值以及峰峰值)与车隧阻塞比之间的关系进行拟合，发现两者之间满足以e为底的指数函数关系，相关系数R2均大于0.9996，如图15所示。

(a)l=100 m

由图15可见，对于隧道壁面不同位置的测点，随着车隧阻塞比的增大，典型气动压力峰值均以指数形式增大。对隧道壁面气动压力正峰值而言，隧道中截面峰值压力随车隧阻塞比的增长速率最大，隧道入口段次之，隧道出口段再次之；对隧道壁面气动压力负峰值与峰峰值而言，隧道中截面峰值压力随车隧阻塞比的增长速率最大，隧道出口段次之，隧道入口段再次之。

4 结语

隧道壁面不同位置测点的初始压力波梯度最大值以及正峰值与车隧阻塞比之间满足以e为底的指数函数关系，相关系数R2均大于0.998；随着车隧阻塞比的增大，初始压力波梯度最大值以及正峰值均以指数形式增大。在高速列车处于阶段2及阶段3时，隧道壁面不同位置测点的典型气动压力峰值(正峰值、负峰值以及峰峰值)与车隧阻塞比之间也满足以e为底的指数函数关系，相关系数R2均大于0.999 5；随着车隧阻塞比的增大，隧道壁面典型气动压力峰值增加量逐渐增大。高速列车处于阶段3时，隧道纵轴中截面典型气动压力峰值随车隧阻塞比的增长速率最大，出口段次之，入口段再次之。在列车车尾驶出隧道出口后，隧道纵轴中截面正峰值压力随车隧阻塞比的增长速率最大，入口段次之，出口段再次之；隧道纵轴中截面负峰值压力随车隧阻塞比的增长速率最大，出口段次之，入口段再次之。

本研究主要分析了车隧阻塞比对隧道壁面气动压力特征的影响规律，后续工作将研究壁面气动压力作用下隧道衬砌结构的动力损伤及残余寿命，进而通过壁面气动压力中间变量来构建车隧阻塞比与衬砌结构动力损伤及残余寿命之间的关系，最终为高铁隧道安全运营提供理论支撑。