网联车混行条件下交通流量融合方法
李潇 汪涛 张毅 李朝阳
(上海交通大学 船舶海洋与建筑工程学院,上海 200240)
智能网联汽车可以通过专用短程通信(Dedicated Short Range Communication,DSRC)[1]、第五代移动通信技术(简称5G)等通信技术实时与道路上的其他车辆和智能路侧设备进行通信,通过将交通数据上传至云端数据中心以进一步实现对交通状态的精确掌握;但是,即使网联车在道路上实现完全普及,采集到的交通数据也需要其他检测手段加以修正,传统交通数据检测仍是保证道路交通数据准确性的重要方式。现有研究表明,至2050年,道路上智能网联车所占比例仅为75%左右[2],因此在智能网联车与人工驾驶车辆长期混行的条件下,如何利用有效的方法对由网联车实时回传的数据和其他利用传统交通信息检测方式获取的数据所组成的多源交通数据进行融合,对实时掌握交通运行状况具有重要意义。
关于智能网联车与多源交通数据的融合,国内外学者已做了大量研究。在网联车数据采集与应用方面,Du等[3]为了获取网联车和周围车辆换道行为的相关数据,基于V2X技术设计了一套高精度的车辆位置信息收集系统,实验表明该系统能准确描述车辆换道轨迹;Sahin等[4]针对网联车集群中的数据自主收集问题构建了一个测试反馈式数据动态收集方法的框架,并建立了一个可以模拟数据动态收集过程和对这一过程中的决策进行评估的仿真平台;Hu等[5]将网联车在行驶过程中所提供的丰富信息结合深度学习对密歇根州某地的公路交叉口进行了事故风险水平预测。在径向基神经网络(Radial Basis Function Neural Network,RBFNN)的应用方面,Ullah等[6]为降低因无线传感器网络传输无效数据而产生的额外功耗,提出了一种基于改进RBF神经网络的数据聚合方法,该方法能够对传感器采集到的数据进行分类并有效减少冗余数据和异常值;Hou等[7]提出了一种结合堆栈自动编码器(Stacked Autoencoder,SAE)和RNF神经网络的短时交通流预测模型,该模型能够有效地拟合交通流的周期性变化,同时降低天气等因素对预测结果的干扰;罗玉涛等[8]提出了一种降低车轮控制系统干扰的自适应神经网络滑膜控制方法,该方法采用RBF神经网络对系统的不确定性和电机力矩的扰动进行实时估计,以此作为车轮转角控制器设计的基础,有效提高了车轮转角控制的自适应性和稳定性。由上述相关研究可以看出,RBF神经网络已得到了广泛应用。
道路交通流量是表征交通运行状态的重要参数,数据的非线性程度较高。RBF神经网络可以逼近任意精度的非线性函数,具有收敛速度快的特点,用于多源交通流量融合具有明显的优势[9];而利用粒子群算法(Particle Swarm Optimization,PSO)的寻优能力确定RBF神经网络中神经元核函数的中心坐标、宽度与权重,可以使其发挥更出色的函数逼近能力。因此,本研究提出使用粒子群算法结合RBF神经网络对多源交通流量进行融合。
1 多源交通数据融合框架
1.1 多源交通数据的特点
智能网联车在行驶的过程中通过DSRC或者5G通信技术与其他网联车和智能路侧设施进行信息实时交互。以此为基础,交通主管部门可以实现对车辆信息的全方位采集,主要体现在对车辆速度、车辆位置、路段车辆密度、车辆OD点对、延误等数据的获取上。以交通流量为例,通过道路上网联车来推算交通流量,在线圈检测、微波检测等传统交通流量检测方式以外,为道路交通流量的准确判断提供了一个新的途径;与此类似,众多研究表明,多源交通大数据从不同维度对城市交通信息进行描绘[10]。混行条件下多源交通数据具有规模性、多样性、实效性、价值性4个基本特点。
1.2 多源交通数据融合框架
交通信息采集与存储一般存在多个数据源系统,导致交通数据本身具有丰富的多样性。各种交通调度平台、交通监测系统中的各种数据相互独立、结构各异、数据量大且分散,使得交通信息不能充分利用。因此在进行多源交通数据融合的同时,还需要对交通大数据进行充分分析、挖掘与提取,从不同数据层面对交通数据进行高效处理,降低数据噪音和冗余度并提高数据的准确性。如图1所示,以网联汽车、路侧交通设施、交通监测系统等数据源提供的数据作为交通数据融合的原始数据,提取数据特征后形成具有指向性的特征数据输入到特征层,特征数据经过特征层的深度融合后经过处理输入到决策层,最终得到交通运行决策数据,以达到利用少量的数据获得尽可能多的交通特征的目的。

图1 网联环境下交通大数据融合框架
2 多源交通流量融合方法
2.1 道路交通流量获取
2.1.1 传统交通数据采集方法
在传统交通数据采集领域,针对道路交通量、平均车速等交通参数的获取主要有人工计数法、浮动车法、机械计数法与录像法等方式。但受限于人力成本与检测器的精度,传统交通数据的调查方法难以做到面面俱到。
2.1.2 网联环境下交通数据获取
若道路中车辆全部为网联车,可以把道路中的全部车辆视为“特殊传感器”。而在网联车与非网联车混行的条件下,在对道路交通流量进行估计时,可以把混行车流中的网联车看作浮动车,利用车载激光雷达或摄像头,结合目标检测技术识别单位时间内超越网联车或被网联车超越的车辆数,采用“浮动车法”进行交通流量检测,将车辆在行驶过程中采集到的数据计算生成交通流量并回传至数据中心,检测计算方法如式(1)所示:
(1)
其中,qc为目标路段选定方向(如某路段下行方向)上的交通量,Xa为网联车逆选定方向(上行方向)行驶时迎面驶来的车数,Yc为网联车顺选定方向(下行方向)行驶时超越网联车的车数减去被网联车超越的车数,ta为网联车逆选定方向(上行方向)的行驶时间,tc为网联车顺选定方向(下行方向)的行驶时间。
针对道路上同一时刻有多辆网联车行驶的情况,测量交通量取多辆网联车返回数据的算术平均值。
2.2 粒子群优化径向基神经网络
2.2.1 径向基神经网络
RBFNN于1988年由耶鲁大学的Moody等[11]提出,该神经网络只有一个中间层,神经元以径向基函数作为核函数,径向基函数图像如图2所示。中间层每个神经元只对特定范围的输入做出响应,对这些响应赋予权重W得到输出值。由于中间层数量少,所以RBFNN的学习速度极快,同时由于每个神经元与输出值的关系相对独立,神经元之间的相互干扰小,适合进行大范围的数据融合以及高速数据处理。
图2 径向基函数图像
2.2.2 粒子群算法
虽然RBFNN结构简单,但是中间层神经元核函数y(x,w,b)=e-(b(x-w))中w和b的确定对减小输出误差和降低隐藏层的维度非常重要[12],实际应用中大多采用穷举、试凑和经验的方法来确定,具有盲目性且效率较低。PSO算法计算过程简单且需要调整的参数少,适用于复杂问题求最优解,算法由Kennedy等[13]于1995年提出,每个粒子在时刻t具有位置xi(t)和速度vi(t)两个参数,首先需要确定整个系统的目标函数以判断粒子优劣,再根据每一轮粒子返回的目标函数值寻找粒子个体最优位置pi和全局最优位置pg,最终得到全局最优位置pg即为系统最优解。
vi(t+1)=k·vi(t)+c1·rand()·(pb,i(t)-xi(t))+
c2·rand()·(gb(t)-xi(t))
(2)
xi(t+1)=xi(t)+vi(t+1)
(3)
其中:vi表示某一个时刻粒子i的速度;k为惯性权重;c1、c2为自身学习因子和社会学习因子;rand()表示0到1之间的随机数。
2.2.3 算法设计
RBFNN在训练过程中需要确定4个关键性参数:中间层神经元个数、每个核函数中心坐标w和宽度b、各神经元的输出权重W。不同类型的数据样本,中间层神经元的个数不同,因此首先选定输入数据组成数据集,后续神经网络中间层核函数维度需与输入数据集维度一致;利用Elbow Method方法和K均值聚类算法对训练集中的数据进行聚类,取聚类中心个数作为神经元的个数,同时聚类中心的坐标还可以作为粒子运动时的范围参考;然后设计对应数量级的神经网络,在求神经网络中的关键参数w、b、W的过程中,引入具有优良寻优性能的粒子群算法对神经网络进行优化,以融合数据与对照数据的差值作为优化的目标函数进行迭代;最后通过粒子迭代以及运算过程中RBFNN自身参数的更新共同得到几个关键参数,计算过程如图3。
2.3 卡尔曼滤波交通流量融合方法
在多源传感器数据融合方面,卡尔曼滤波(Kalman Filter,KF)是一种最优的系统参数估计方法[14]。传统卡尔曼滤波算法的核心是预先将非线性系统中的非线性函数变换为线性函数,使用反馈控制来不断迭代估计整个系统的状态,在数学上是一种线性最小方差统计估算方法[15]。车辆的到达在某种程度上具有随机性,这种随机性反映在空间和时间两个维度上呈现线性或非线性分布,因此本研究使用PSO-RBFNN和KF两种方法对多源交通流量进行融合,并对这两种方法的融合效果进行了对比。
3 算法验证与分析
3.1 数据来源
对来源于不同交通检测设备的数据进行融合,在某市实验路网中选取一段东西双向六车道路段,在目标路段距离交叉口停车线25 m处安装微波与视频检测装置,在距离交叉口停车线5 m处安装线圈检测器,浮动车数据由测试网联车回传。选择其中3种检测方式测得的道路交通流量:线圈检测获取的交通流量qc,“浮动车法”获取的交通流量qf,微波检测设备获取的交通流量qm,由于网联车混行条件下可以将网联车视为浮动车,将qf作为混行条件下网联车计算的交通流量,剔除明显错误数据后整理得到3组Excel数据,交通流量取每天07:00-09:00以及17:00-20:00的高峰流量,以15 min为时间间隔进行划分。设计的神经网络中以qc和qf两种数据作为输入进行融合,并以微波检测设备获取的交通流量qm表征实际道路交通流量,作为对照组对融合后的数据进行对比。为训练本段道路交通流量对应的神经网络,将上文采集到的交通流量数据划分为训练集和测试集两部分,同时取前70%的数据作为训练集、后30%的数据作为测试集。

图3 粒子群优化的径向基神经网络示意图
3.2 PSO-RBFNN算法数据融合
3.2.1 神经网络训练
使用Matlab编写算法程序,首先利用“Elbow Method”对训练集中的数据进行聚类中心分析[16],以确定中间层神经元的个数进行判断,将线圈检测装置和“浮动车法”获取的交通流量进行组合,形成二维数据点对,形式为“(线圈检测数据,浮动车获取的数据)”,将数据对看作二维平面上的点,利用K-Means算法将数据分为3类(基于K聚类的交通流量分类结果如图4所示),中心点分别为(217.344 6,210.588 1)、(214.678 2,238.514 9)、(240.261 2,226.765 6),并以聚类中心为参考设置本轮RBF神经网络中间层神经元中心位置的移动范围。

图4 基于K均值聚类的交通流量分类
然后用PSO算法生成20个粒子,结合3个聚类中心坐标对粒子初始坐标范围和运动范围进行框定。由于RBFNN共有3个神经元,每个神经元有2个中心点参数:1个宽度参数和1个权重参数,因此粒子的维度设12。
最后建立PSO-RBFNN目标函数,将3种方式获取的交通流量输入神经网络,利用qc和qf进行融合,将融合结果与qm的差值作为PSO算法中粒子优劣的目标函数,通过迭代最终得到最优粒子,PSO-RBFNN迭代曲线如图5所示。
从图5可以看出,将融合的交通流量与微波检测的交通流量进行比较,随着训练次数的增加,差值逐渐缩小。经过1 400轮迭代,最终输出粒子的12个维度坐标即为RBFNN中的参数,其中,第1、2;5、6;9、10个参数为神经网络神经元中心坐标,分别为(227.988 3,223.000 0)、(229.332 0,230.785 9)、(207.000 0,220.000 0),第3、7、11个参数为神经元核函数的宽度;第4、8、12个参数为神经元权重。这一RBF神经网络可作为本次实验路段最终交通流量融合的神经网络。

图5 PSO-RBFNN迭代曲线
3.2.2 交通流量融合
选取路段交通流量中的测试集,利用3.2.1节中训练得到的RBF神经网络,将线圈获取的交通流量qc与浮动车获取的交通流量qf作为输入进行融合,再将融合后的结果与微波检测器获取的交通流量进行对比,结果如图6、图7所示。
从图6中可以看出,经过PSO-RBFNN融合得到的数据围绕两组参与融合的基础数据qc和qf波动,但在图7中,将表征实际情况的数据qm添加到图中后,可以明显地看出融合后得到的数据曲线与qm的曲线更加贴合,即PSO-RNFNN融合结果与实际情况更相近。这是因为在神经网络训练过程中,目标函数值的确定依赖于qm。

图6 PSO-RBFNN交通流量融合结果

图7 PSO-RBFNN交通流量融合结果与对照组对比
3.3 卡尔曼滤波算法数据融合
同样,将3.1节中测试集数据中线圈检测获取的交通流量qc与浮动车检测获取的交通流量qf输入到KF中,得到两者融合的数据,再将经过融合的数据与微波检测器获取的交通流量进行对比,结果如图8、图9所示。

图8 KF交通流量融合结果

图9 KF交通流量融合结果与对照组对比
从图8中可以看出,经过KF融合后得到的数据始终处于两组参与融合的基础数据qc和qf之间,在图9中加入表征实际情况的数据qm后,融合后的数据曲线与真实数据曲线关联性不明显,因为经过KF融合后获得的数据仅与qc和qf有关。
3.4 误差分析
不同分布特征的数据可以采用不同的融合方式,数据融合方式没有优劣之分,只有适用情况不同。本节采用PSO-RBFNN神经网络和KF两种方法分别对不同检测方式获取的交通流量进行融合。对两种方式的融合结果分别采用平均绝对误差(MAE)、平均绝对百分误差(MAPE)和均方根误差(RMSE)3个指标评价两种方式的数据融合效果,结果如图10、表1所示。

图10 KF与PSO-RBFNN融合效果曲线
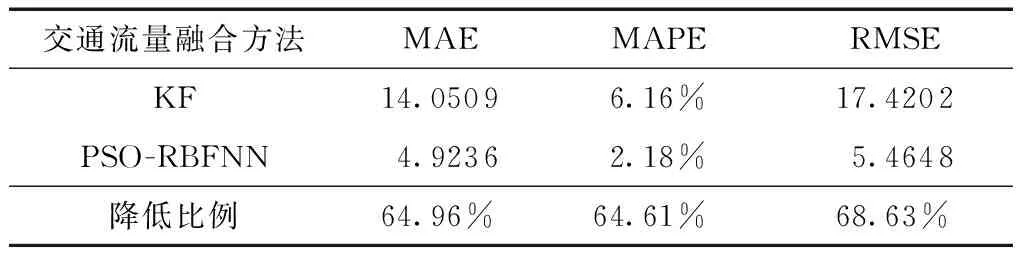
表1 PSO-RBFNN与KF融合效果对比
通过图10和表1可以看出,PSO-RBFNN的融合结果曲线与对照数据曲线更加贴合,各项误差值也显著降低。因此,利用PSO-RBFNN融合两种来源的交通流量更加贴近对照组的结果,这是由于PSO-RBFNN融合的数据在训练过程中以对照组数据为参考,融合效果更好,即:PSO-RBFNN能凭借粒子不断迭代更好地提取所拟合目标的现实特性,在数据融合与预测中具有更高的精度。
4 结论
网联车与非网联车混行产生的交通大数据具有规模性、多样性、实效性、价值性等特点,通过粒子群算法寻优和利用不同来源的道路交通流量对径向基神经网络进行训练,可以看出,利用K均值聚类法对初始多源交通数据进行分类可以有效确定神经网络中间层个数,减少径向基神经网络的空间复杂度;在多轮粒子迭代过程中随着神经网络中参数的不断调整,融合交通流量与实际交通流量的差值逐渐缩小并趋于稳定,神经网络逐渐拟合该段道路交通流量的分布特征;同时此方法融合后的数据与卡尔曼滤波算法融合后的数据相比误差相对更小,对非线性数据的融合过程更具有针对性,明显提高了交通状态的拟合度。

