考虑换乘客流的城市轨道交通网络末班车衔接优化研究

郑亚晶 李耀辉 靳文舟

(华南理工大学 土木与交通学院，广东 广州 510640)

随着我国城市轨道交通的飞速发展，城市轨道交通网络中各条线路末班车乘客的换乘协调问题受到了越来越多的关注。一般来说，由于城市轨道交通网络上各条线路的运营时间有一定差异，在末班车时段，乘客通过城市轨道交通网络出行的可达性会因为各线路逐步结束运营而出现变动，无论怎样确定各换乘站末班车的推算顺序及衔接关系，总会有部分乘客因赶不上换乘线路的末班车而无法依靠城市轨道交通完成出行。在此情形下，通过调整城市轨道交通末班车在换乘站的衔接关系，将因赶不上换乘线路末班车的换乘乘客人数最小化，是针对这一问题相对较好的解决方案。

目前，关于城市轨道交通网络中各条线路末班车之间的衔接研究，已成为一个热点。Kang等[1- 5]以换乘站成功方向数最大为目标，构建了针对末班车的时刻表优化模型，并设计了遗传算法求解；徐瑞华等[6]借鉴最小生成树Kruskal算法的基本思想，提出了考虑客流需求及运营者的特定衔接需求的网络末班车衔接方案优化算法；郭建媛等[7]提出了路网可达性与OD对最晚可达时间的计算方法；袁振洲等[8]以乘客换乘感知费用总和最小为目标构建了全网条件下末班车时段多趟列车的时刻表衔接优化模型，并设计了多种群遗传算法进行求解；Chen等[9]通过延长换乘站停站时间，建立了以换乘成功客流量最大为目标的末班车时刻表优化模型；温芳等[10]在考虑运营结束延迟惩罚的基础上构建了以提高时段内各间隔起始时刻的关键OD可达对数之和为目标的数学模型，并据此对各线路的末班车发车时刻进行了优化。

从既有研究来看，研究者主要是在确定换乘站末班车停站衔接关系的基础上进行各线路末班车开行时刻表的制定；换句话说，确定各条线路的换乘客流上下行在换乘站的换乘衔接关系，是协调编制城市轨道交通网络中各条线路末班车计划的前提。不过在网络化运营条件下，各个城市的城市轨道交通网络具有规模大、换乘站数量多、换乘关系复杂等特点，换乘客流在各换乘站的换乘衔接关系相互制约、相互影响，制定全网络最合理的末班车客流换乘站衔接方案难度很大；故目前对末班车客流在换乘站的衔接方案的研究成果还存在关键OD的选取主观性太强、求解中对模型松弛过大等问题。基于此，本研究在建立城市轨道交通末班车换乘衔接关系网络的基础上，通过求解该网络的最大有向无环子图，从而确定换乘人数最大的末班车换乘衔接方案，并通过算例，对这一模型进行验证。

1 换乘衔接网络

1.1 换乘站内部的衔接网络

我国的城市轨道交通线网中，承担两条线路换乘的两线换乘站是最常见的，这类换乘站一般需要负责8个方向的换乘客流。由于每条运营线路都由上下行两个方向组成，因此这8个方向的换乘客流可由代表线路和上下行的4个节点以及它们之间的8条有向边表示，如图1(a)所示，其中，v1(a)，1和v1(a)，2分别表示换乘站a中线路1的上、下行方向站台停靠的末班车，v2(a)，1和v2(a)，2分别表示换乘站a中线路2的上、下行方向站台停靠的末班车。承担多线换乘任务的换乘站与两线换乘站类似，图1(b)所示为三线换乘站中换乘流向的示意。为描述方便，本研究中，将图1中这种换乘站内部的换乘客流衔接有向边称之为“换乘边”。

(a)两线换乘站

1.2 线路中换乘站之间的衔接关系

确定线网中末班车换乘客流的衔接方案，实质上是确定各线末班车在换乘站的到站时间先后顺序关系。由于在城轨网络中，一条线路会包括若干换乘站，该线路上的末班车在这些换乘站会因上下行关系存在固定的时间先后顺序，如图2(a)中目标线路中的两个换乘站a和b，上行方向末班车到达a站的时间一定早于b站，下行方向末班车到达b站的时间一定早于a站，也即从乘客的角度来看的话，这两个站之间的乘客换乘流线，可由4个节点和它们之间的2条有向边表示(如图2(b)所示，v1(a)，1和v1(a)，2分别为目标线路在换乘站a的上、下行方向站台停靠的末班车；v1(b)，1和v1(b)，2分别为目标线路在换乘站b的上、下行方向站台停靠的末班车)。为描述方便，本研究中，将图2示意的这种代表同一线路不同换乘站之间乘客流的有向边称之为“列车边”。

(a)实际线路方向

1.3 衔接关系的逻辑约束

针对某一城市轨道交通网络系统，按文中第1.1节及1.2节构建换乘站内的换乘边与同一线路换乘站间的列车边即可得到该城市轨道交通末班车的换乘衔接关系网络，这一网络可近似视为末班车乘客在整个城轨系统中客流的可能流向集合。在这一网络中，列车边由列车的行驶方向确定，是客流在乘坐列车时随列车开行的行进方向；而换乘边之间则存在着互相制约关系：一条换乘边代表的客流换乘方向是否能实现，必须考虑其他换乘边所代表的客流换乘方向是否能实现，换句话说，换乘边之间存在着复杂的取舍关系，而这之中，不同决策目标下的不同取舍方案，即为城市轨道交通系统中不同的末班车衔接方案。

换乘边一般会成对出现，其衔接关系可归纳成3种情况[6]：双方向衔接、单方向衔接和无方向衔接。双方向衔接是指成对的两条换乘边所代表的两个方向的末班车换乘乘客均能顺利互相换乘，如图3(a)所示；单方向衔接是指在成对的两条换乘边所代表的两个方向的末班车换乘乘客中，仅一个方向的乘客可以顺利完成换乘，如图3(b)所示；无方向衔接是指成对的两条换乘边所代表的两个方向的末班车换乘乘客均不能顺利完成换乘，如图3(c)所示。由于双方向衔接需要至少有一个方向的末班车停站时间超过换乘乘客的换乘时间，考虑到地铁的运行效率及末班车收班后的检修作业，这一情形应该尽量避免，因此对于换乘站的内部衔接关系来说，两条成对的换乘边在最后的衔接方案中往往是无法同时存在的，也即在最后的衔接方案中，两条成对的换乘边最终会以单方向衔接和无方向衔接的形式出现。

(a)双方向衔接

若将以上对成对的换乘边的分析进行扩展，对于城市轨道交通末班车换乘衔接关系网络来说，任何由有向边组成的“回路(环)”的接续关系都不可能被全部满足，否则就意味着末班车的乘客在进行多次换乘接续以及乘坐后，仍然能在原下车站乘坐上该末班车，这显然与城轨列车在车站短暂的停站时间相矛盾。

因此，确定网络末班车衔接关系，其实质就是从衔接关系集中选出不会组成“回路(环)”的最大客流衔接关系子集，也即求城市轨道交通末班车换乘衔接关系网络的最大有向无环子图。

2 网络末班车衔接方案优化模型

2.1 网络表示

2.2 有向图中的无环概念

在图论中，如果一个有向图无法从某个顶点出发经过若干条边回到该点，则该图是一个有向无环图。有向图中的无环与无向图中的无环有较大区别，例如图4(a)和图4(b)，一个为有向图，一个为无向图，虽然在视觉上这两个网络图结构一样，但图4(a)无环，图4(b)则有环。由于有向图中一个点经过两种路线到达另一个点也未必形成环，因此有向无环图未必能转化成树，故无向图中求解无环子图的“避圈法”或“破圈法”均无法在此运用。

(a)有向图

2.3 模型构建

根据图论的相关知识，任何一个有向无环图都可转化为其顶点的一个线性序列，该线性序列满足以下两个条件：

①每个顶点出现且只出现一次；

②若存在一条从顶点A到顶点B的路径，那么在序列中顶点A出现在顶点B的前面。

这一顶点序列称为该有向无环图的拓扑排序[11]，一般来说，一个有向图可以有一个或多个拓扑排序序列；反过来，在有向图中，将其所有顶点进行随机排序，然后仅保留该序列中符合拓扑序列规则的边，即可得到原有向图的一个与该顶点序列对应的有向无环子图。据此，可定义整数变量ui(n)，a表示有向图G=(V，E)某个顶点排序中节点vi(n)，a的序号，显然，该顶点排序与对应的有向无环子图的有向边关系如下：

(1)

其次，换乘客流仅能在列车边和换乘边中实现，故

(2)

此外，列车边的客流是必须存在的，能够调整的仅仅是换乘边，则有

(3)

本研究以考虑换乘客流为前提，故将可成功换乘的乘客人数最多作为目标，目标函数式如下所示：

(4)

至此，模型构建完毕。

3 模型求解

本研究构建的模型为非线性整数规划模型，传统方法较难求解，考虑到有向无环子图与顶点的拓扑排序的对应关系，文中提出一种基于有向图顶点拓扑排序编码染色体的遗传算法对模型进行求解。

一般来说，对于类似文中的网络路径问题，采用普通的二进制编码，以0- 1分别表示对应的边是否在最终路径之中的编码方式，在进化过程中染色体往往无法表达一个合法的路径，因此文中采用的编码，是在“基于优先级编码[12]”的基础上通过加入列车边的客流方向实现，具体编码过程如下：

步骤1将顶点集V中的顶点按列车边形成的链(文中称为“列车链”)进行分组，并从1开始给每个分组一个组号。

步骤2将所有顶点进行随机排序后再用组号进行替换。

通过以上两个步骤，即可得到一条可行染色体，染色体长度等于顶点集V中的顶点数，每条染色体表示有向图G=(V，E)的一个有向无环子图。

例如图5(b)就是图5(a)所示线网的换乘衔接关系网络，在该网络中，列车链共4条(v1(a)，1-v1(b)，1，v2(a)，1-v2(b)，1，v1(b)，2-v1(a)，2，v2(b)，2-v2(a)，2)，按列车链对顶点进行分组：第1组节点为v1(a)，1、v1(b)，1，第2组节点为v2(a)，1、v2(b)，1，第3组节点为v1(b)，2、v1(a)，2，第4组节点为v2(b)，2、v2(a)，2；将这8个节点随机排序并用其所在组号替代，即可得到一个染色体。例如“1- 2- 3- 1- 2- 4- 3- 4”即为一个染色体。

(a)线网

(b)换乘衔接关系网

而在对染色体进行解码时，只需先将每组顶点按“列车接续边”的方向进行组内排序，再将每组顶点按组号及组内顺序，从左至右顺次替换染色体中的数字。

例如解码染色体“1- 2- 3- 1- 2- 4- 3- 4”时：左边第1位上的基因片段“1”，是“1”在这个染色体中第1次出现，即替换为组1中的第1个顶点；第2位上的基因片段“2”，是“2”在这个染色体中第1次出现，即替换为组2中的第1个顶点；第3位上的基因片段“3”，是“3”在这个染色体中第1次出现，即替换为组3中的第1个顶点；第4位上的基因片段“1”，是“1”在这个染色体中第2次出现，即替换为组1中的第2个顶点；剩下的编码均按此规则进行替换，也即该染色体可替换为“v1(a)，1-v2(a)，1-v1(b)，2-v1(b)，1-v2(b)，1-v2(b)，2-v1(a)，2-v2(a)，2”；再在原始有向图G=(V，E)中，仅保留与“v1(a)，1-v2(a)，1-v1(b)，2-v1(b)，1-v2(b)，1-v2(b)，2-v1(a)，2-v2(a)，2”从左至右方向一致的“列车接续边”和“换乘接续边”，此时，即得到有向图G=(V，E)的一个无环子图，如图6所示。

图6 线网的一个有向无环子图

至此，染色体“1- 2- 3- 1- 2- 4- 3- 4”解码完成。

本研究构建的模型为单目标，可直接将染色体对应的目标值的排序作为评价函数的计算依据，利用式(5)计算染色体Zi的评价函数[13]

eval(Zi)=θ(1-θ)i-1

(5)

式中：i为该代种群中，染色体按式(4)计算的目标值的降序排列；θ为给定的参数，值取在0和1之间，在文中算例中取0.02。

此外，由于文中构建的染色体中的基因片段的前后关系与接续方案密切相关，因此本研究的交叉操作建议采用类OX法[14]进行。例如有两父代染色体A和B，随机选择一个匹配区域：

A=1- 2|3- 1- 2- 4|3- 4，

B=2- 4|1- 1- 2- 4|3- 3。

将A的匹配区域加到B的前面，B的匹配区域加到A的前面，得到：

A′=1- 1- 2- 4|1- 2- 3- 1- 2- 4- 3- 4，

B′=3- 1- 2- 4|2- 4- 1- 1- 2- 4- 3- 3。

然后在A′和B′中自匹配区域后依次删除与匹配区域中相同的基因片段，得到最终的两个子串：

A″=1- 1- 2- 4- 3- 2- 3- 4，

B″=3- 1- 2- 4- 1- 2- 4- 3。

文中算法对变异操作并无要求，采用经典的对换变异(即随机选择染色体中的两个基因片段，将其进行交换)即可。

4 算例

图7为一城市轨道交通线网图例，一共4条线路，其中L4为环线，线网共包含6个换乘站{a，b，c，d，e，g}，其中a站为3线换乘站，其他站为2线换乘站。

图7 城市轨道交通网络

根据客流统计数据，在该地铁网络的末班车运行时段，列车与列车之间换乘客流的数据如表 1-表6所示。

表1 a站的换乘客流流量

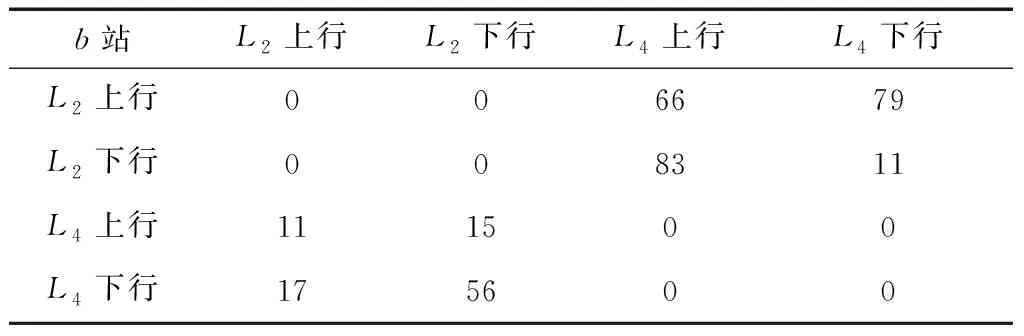
表2 b站的换乘客流流量

表3 c站的换乘客流流量

表4 d站的换乘客流流量

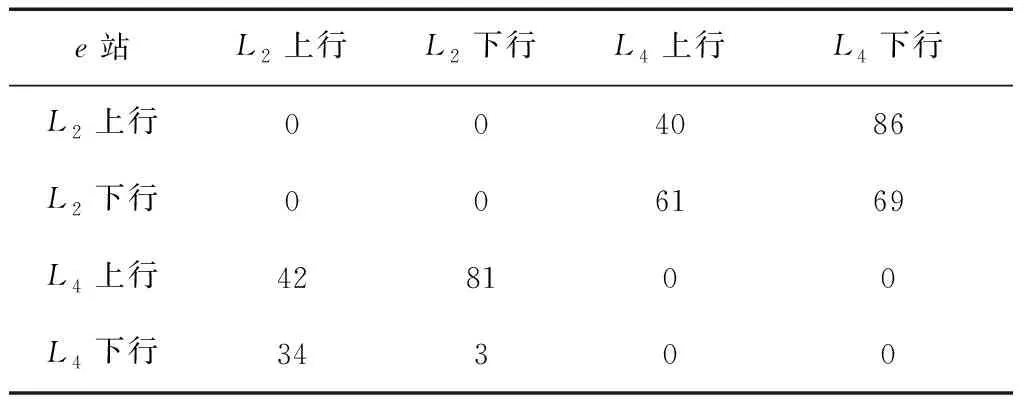
表5 e站的换乘客流流量

表6 g站的换乘客流流量

利用第1节的方法，可将该地铁网络转化为换乘衔接网络，结果如图8所示。

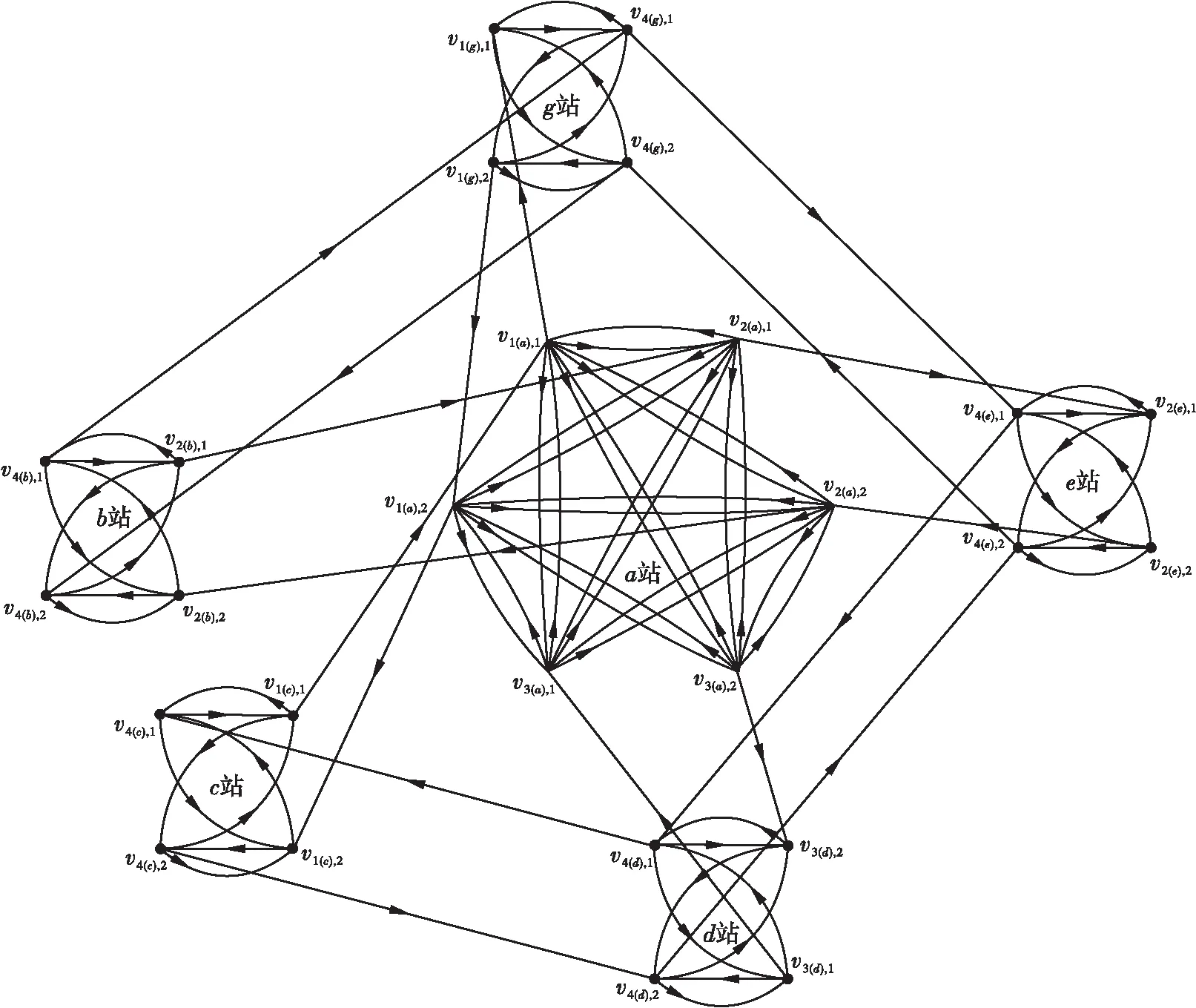
图8 线网转化的换乘衔接网络

图8中的26个顶点共组成8条列车链，具体如表7所示。

表7 列车链

种群规模100，进化160代，交叉概率取0.95，评价函数中参数θ取0.02，为避免种群早熟，变异概率线性变化，在开始时取0.000 1，160代时取0.1。运行10次，10次求解中种群的收敛情况如图9所示，其中的最好结果为2 143。而利用随机游走算法[15]游走10 000 000步，最好结果为1 558，即便在文中构造的初始种群的基础上再利用随机游走算法游走10 000 000步，得到的最好结果也仅为2 108，这说明文中采用的遗传算法有较好的优化效果；而从种群收敛情况来看，算法进化30～60代种群即开始保持稳定，这说明文中采用的遗传算法具有良好的鲁棒性。

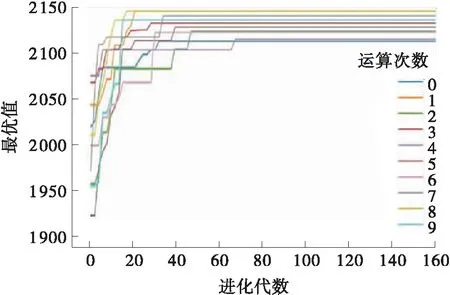
图9 遗传算法种群收敛图

在以上的10次计算中，最优染色体为“5- 8- 1- 5- 3- 3- 7- 8- 3- 1- 4- 1- 5- 1- 6- 4- 1- 6- 4- 2- 2- 2- 2- 7- 2- 6”，对其进行解码，可得到对应的顶点排序为“v2(b)，1-v3(d)，1-v4(b)，1-v2(a)，1-v1(c)，1-v1(a)，1-v3(a)，2-v3(a)，1-v1(g)，1-v4(g)，1-v1(g)，2-v4(e)，1-v2(e)，1-v4(d)，1-v2(e)，2-v1(a)，2-v4(c)，1-v2(a)，2-v1(c)，2-v4(c)，2-v4(d)，2-v4(e)，2-v4(g)，2-v3(d)，2-v4(b)，2-v2(b)，2”，将该排序解码后，即可得到最终各换乘站点保留的换乘衔接关系，如表8所示。

表8 线网各换乘站的末班车衔接关系表

以表8中的换乘衔接关系为基础，依据各线路列车运行的相关参数，即可逐步对全网络各线路的末班车时刻表进行推算。

5 结语

城市轨道交通各线路末班车之间乘客换乘协调问题的实质是确定各换乘站末班车之间的推算顺序及衔接关系。本研究以末班车成功换乘乘客人数最大化为优化目标，提出了网络末班车的衔接方案优化模型和算法，通过该算法可最终得到整个城市轨道交通网络的末班车换乘乘客衔接关系表。基于该关系表，即可对各线路的末班车在换乘站的经过时刻先后进行判定，并据此计算出各线路末班车的始发时刻及在所有车站的到发时刻。但需要说明的是，城市轨道交通网络末班车计划的编制需要考虑的因素较多，换乘乘客的人数最大化只是其中较重要的一项考虑因素，故文中的这一方法只可作为末班车计划编制的辅助手段，为城市轨道交通网络中各线路末班车时刻表的编制提供一定的决策依据。