装配式钢-混凝土组合框架动态倒塌性能研究

杨涛 黄俊人 张云 庞瑞文

(1.广西大学 土木建筑工程学院，广西 南宁 530004；2.广西大学 工程防灾与结构安全教育部重点实验室，广西 南宁 530004；3.广西北投公路建设投资集团有限公司，广西 南宁 530022)

2021年，我国江苏省苏州市吴江区的四季开源酒店辅房和美国佛罗里达州迈阿密-戴德县的一处公寓先后发生了倒塌事故[1- 2]，这些事故再次表明了对建筑结构开展抗倒塌设计的重要性。钢-混凝土组合框架结构在多高层建筑中应用广泛，国内外学者针对其连续倒塌性能展开了大量的理论与试验研究。Yang等[3]探讨了采用不同类型的半刚性节点组合框架结构的抗倒塌性能，结果表明结构极限承载力始终由梁柱节点失效所控制。Wang等[4- 5]分析了钢框架和钢-混凝土组合框架子结构中不同抗力机制对结构承载力的贡献。Fu等[6- 7]研究了组合楼盖体系的荷载传递机理及破坏模式，研究表明在小变形阶段，竖向荷载主要通过次梁向相邻柱传递，而在大变形阶段，竖向荷载主要通过主梁和组合楼板进行传递。高山等[8]则提出了组合框架结构中压拱效应和拉膜效应的简化计算模型。

Wang、Zhang等[9- 10]对组合楼盖体系开展的研究表明，混凝土板的拉膜效应在提高结构抗倒塌承载力上发挥着重要作用。谭政等[11]研究表明组合楼板可以使框架子结构在梁机制和悬链线机制的峰值荷载提高54%和117%。Yang等[12]研究了在楼板设置洞口对组合楼盖体系抗倒塌性能的影响，结果表明楼板开洞会明显削弱楼板中的拉膜效应。梁纬球等[13]利用有限元方法分析了跨高比等设计参数对体外预应力组合梁抗倒塌性能的影响，研究表明施加体外预应力可以有效促进结构悬链线效应的产生和发展。钟炜辉和任鲁明等[14- 15]研究了边界约束对框架子结构抗倒塌性能的影响，研究表明结构抗倒塌承载力随着轴向约束的增加而提高。此外，部分学者采用数值方法分析了梁柱连接强度和刚度对组合楼盖抗倒塌性能的影响[16- 17]，研究表明连接刚度对梁中轴力的发展程度影响显著。

随着我国建筑产业化的发展，装配式钢-混凝土组合梁在工程中的应用逐渐增多；近年来，业内学者针对装配式组合梁开展了相关研究[18- 20]，但是现有研究主要集中在装配式组合梁的受力性能方面，对采用装配式组合梁的组合框架结构的抗倒塌性能研究仍鲜见报道。

采用装配式组合梁的组合框架的抗倒塌性能会受到梁中预制板分段位置、预制板拼缝处理方式等因素的影响，倒塌过程中荷载在框架结构内的传递方式以及结构的抗倒塌行为必将呈现一些新的特点。因此，对装配式钢-混凝土组合框架的动态倒塌行为进行研究，具有重要的工程实际意义。为此，本研究首先设计了2个缩尺的采用装配式组合梁的单层两跨的框架子结构试件，通过动态抽柱试验研究了此类框架结构在不同倒塌荷载工况下的动态倒塌行为，并评估预制混凝土板分段对框架动态倒塌行为的影响；然后，基于试验结果建立了装配式组合框架倒塌荷载等效动力增大系数DIF的计算模型，以期为开展装配式组合框架静力倒塌分析时倒塌荷载的修正提供参考。

1 试验概况

1.1 试件设计

参照文献[21]中5层钢-混凝土组合框架，按照1：3的缩尺比例设计2个单层两跨的钢-混凝土组合框架子结构试件，分别记为CB1和CB2。原型结构中组合梁跨度为7 800 mm，层高3 300 mm；楼面永久荷载和活荷载标准值分别为2.5 kN/m2和3.0 kN/m2，如图1所示。

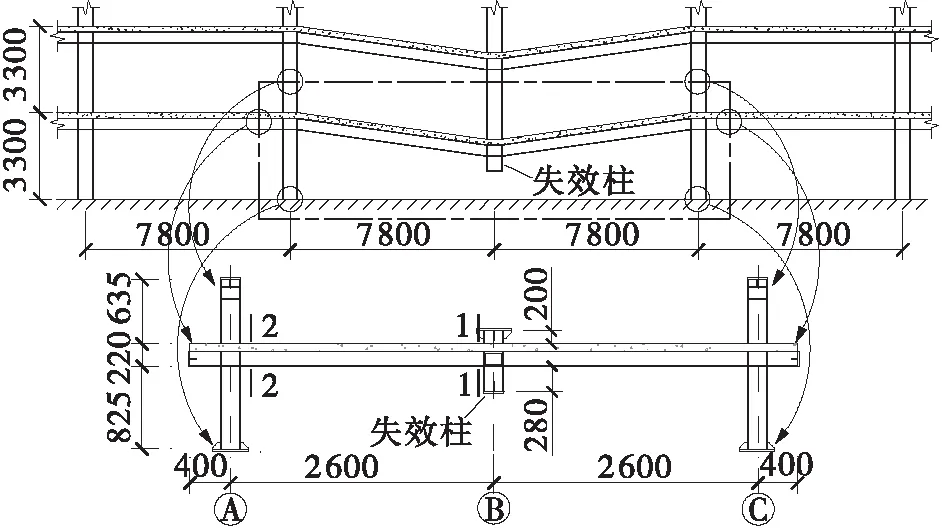
图1 组合框架子结构示意图(单位：mm)

试件CB1的组合梁采用整块预制混凝土板，如图2(a)所示。试件CB2的预制板分段预制，在距离边柱中轴线1 000 mm的位置(约1/3梁跨)处将混凝土板分段，如图2(b)所示；在拼缝两侧的混凝土板顶和板底各布置2块220 mm×180 mm×8 mm(长×宽×厚)的拼接钢板。在与拼缝相邻的每块预制混凝土板的板端预设4个螺栓孔，相邻两预制板的板端利用M16×140 mm(螺栓直径×长度)的高强螺栓通过连接盖板将预制混凝土板拼接在一起。沿框架梁长方向，在预制板上设置两列间距为150 mm的螺栓孔，并采用M16×120 mm的高强螺栓作为抗剪连接件。为了实现预制板内螺栓孔的精确定位成型，在预制板板底与钢梁上翼缘对应的部位设置了8 mm厚的Q235级定位钢板，在定位钢板上焊接内、外直径分别为 18 mm 和22 mm的Q345级无缝钢管，如图2(c)所示。螺栓抗剪连接件的布置数量满足完全抗剪连接的要求。预制混凝土板中的钢筋均采用直径10 mm的HRB400级热轧带肋钢筋，钢筋单层布置。

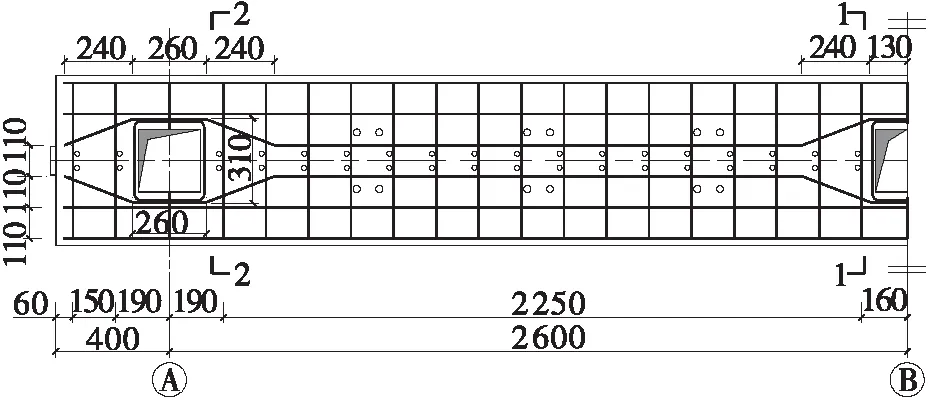
(a)CB1

以试件CB2为例说明预制板与钢梁、相邻预制板之间的拼接等构造措施，如图3所示。为实现混凝土板的预制装配，在混凝土板与柱子交接处设置了边长为220 mm的方形孔洞，预制板内的纵向钢筋在洞口处采用了弯折处理；为避免预制板洞口发生局部破坏，在洞口周围布置了一个直径10 mm的310 mm×260 mm(长×宽)的矩形补强筋；钢柱和预制板预留孔之间的缝隙未进行特殊处理。钢框架由Q235级热轧H型钢加工而成，其中：钢梁采用的型钢规格为HM 150 mm×100 mm×6 mm×9 mm，钢柱采用的型钢规格为HW 200 mm×200 mm×8 mm×12 mm；梁柱节点采用焊脚为8 mm的角焊接连接。实测混凝土轴心抗压强度和弹性模量分别为39.3 MPa和4.26×104MPa；钢材力学性能实测值见表1。

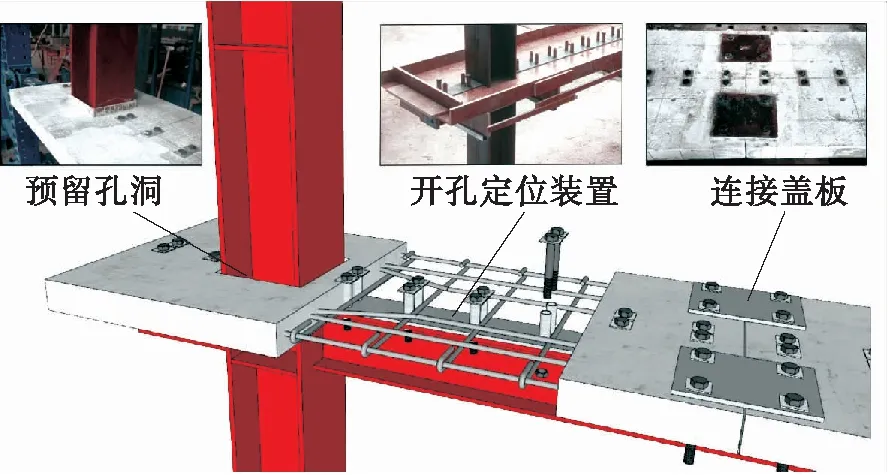
图3 CB2梁柱节点示意图

表1 钢材力学性能

1.2 加载方案

试验加载装置如图4所示。边柱的柱底通过高强螺栓与支座连接，支座通过地锚固定在实验台座上。框架梁端以及上层边柱距离预制板顶505 mm的位置通过高强螺杆与A字形反力架连接，用以模拟相邻结构对试验子结构的约束。

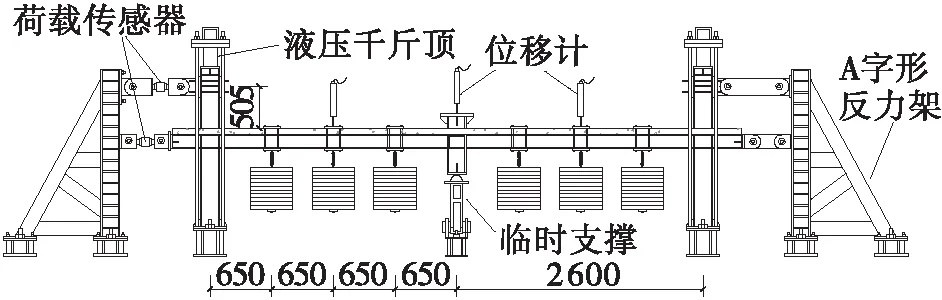
图4 试验装置(单位：mm)

试验中在边柱柱顶施加440 kN的轴向压力，按照钢柱屈服强度实测值计算得到轴压比为0.27。参照DoD[22]规范，楼面荷载取1.2×恒载+0.5×活载，并将上述荷载等效为作用于梁跨4分点上的集中荷载。试验中考察两种工况，即：在每跨梁的4分点上分别悬挂500 kg和1 000 kg的钢配重，用以模拟1倍倒塌荷载(30 kN)和2倍倒塌荷载(60 kN)。

悬挂配重前在中柱设置临时钢支撑，试验时通过悬挂于反力架上的小钢梁撞击中柱下的临时支撑实现快速抽柱。

1.3 测量方案

分别在失效柱及框架梁跨中位置布置传感器，测量子结构在抽柱前、后的频率和阻尼等动力特性，以及抽柱后结构的动态位移响应。

在靠近失效柱和边柱的梁端截面(图1中1—1与2—2截面)的纵向钢筋、钢梁翼缘处布置应变测点，如图2(c)所示，其中：R1为钢筋应变测点，S1和S2分别为钢梁上、下翼缘应变测点；沿梁长方向布置LVDT位移计记录梁的动态位移响应。

此外，在A字形反力架与试件之间设置两个拉压式荷载传感器(如图4所示)，用以测量结构在倒塌过程中反力装置所提供的水平反力。

2 试验结果

2.1 30 kN倒塌荷载工况

快速抽柱后，2个试件在混凝土板顶面的螺栓孔间形成了沿梁跨度方向的贯通裂缝。此外，试件CB1在靠近边柱内侧的混凝土板顶面出现了一条从预制板上的方形孔洞延伸出的细微横向裂缝；试件CB2未观察到类似现象。组合框架在轻微振动后逐渐静止，CB1和CB2在失效柱处的最大动态竖向位移分别达到3.97和4.46 mm。由于振动停止后在2个试件上均未观察到其他明显的结构损伤，结合钢梁和钢筋的应变数据判定整个子结构仍处于弹性工作阶段。图5(a)为CB2在抽柱完成且振动停止后的受力形态。

2.2 60 kN倒塌荷载工况

在60 kN荷载作用瞬间，组合框架梁的振动幅度明显，且振动时间明显变长。抽柱后观察到CB1靠近边柱内侧的混凝土板顶面新增3条裂缝；在CB2靠近边柱的混凝土板顶面新增2条横向裂缝，如图5(b)所示。除此之外，未观测到其他明显的结构损伤。CB1和CB2在失效柱处的最大动态竖向位移分别为10.10和9.84 mm。

(a)30 kN

3 试验结果分析

3.1 失效柱动态位移响应

抽柱后2个试件失效柱在不同配重下的动态竖向位移时程曲线如图6所示。

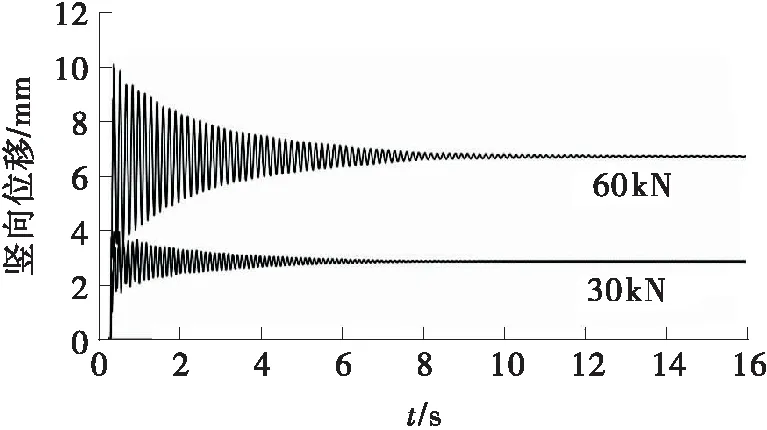
(a)CB1

对比图6可知，悬挂60 kN配重时结构振动幅度明显增大，结构从开始振动到最终停止的时间显著增长；而在相同配重作用下，CB2的振动时长大于CB1。由于混凝土板分段预制拼装是上述2个试件唯一不同的设计参数，而结构的振动时长与所受阻尼力密切相关。因此，当混凝土板分段预制并采用本研究中的拼缝处理方式时，组合框架在倒塌过程中所受的阻尼力将有所降低，结构的振动时长相应增大。

试件CB1和CB2在失效柱处的动态竖向位移响应如表2所示，其中：Δd，max为最大动态位移；Δs为静止后的位移；βΔ=Δd，max/Δs为位移增大系数。对比可知，在30 kN和60 kN配重作用下，CB2的位移增大系数依次为CB1的1.20倍和1.01倍。由此可见，预制混凝土板分段设置后，30 kN倒塌荷载引起的位移增大系数增长明显，荷载的冲击效应最为显著；而60 kN倒塌荷载下预制板是否分段对结构的动态位移增大系数影响不大，这与钢配重增加引起的制振作用有关。在抽除中柱后，钢配重将与框架子结构一起振动；由于重力作用方向始终与框架恢复力方向相反，增大钢配重将起到明显的制振作用。

表2 失效柱处的竖向位移响应

3.2 失效柱加速度响应

图7所示为失效柱处的加速度时程曲线，其变化特征可用图8所示的简化曲线予以描述，其中加速度向上为正、向下为负。

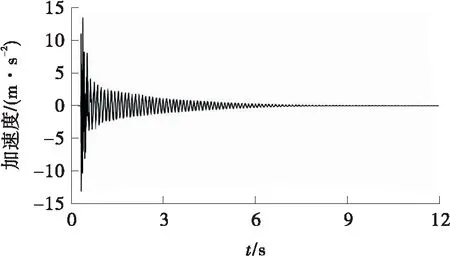
(a)CB1- 30 kN

由于临时支撑与试件之间具有一定的接触压力，在抽除临时支撑的瞬间会对试件产生一个瞬时顶起作用，在曲线中表现为第一个正向加速度峰值(A点)；失效柱向上移动到最高点位置后，在倒塌荷载和结构恢复力的合力作用下，加速度出现第一个负向峰值点(B点)；当失效柱运动至最低点，结构向上的恢复力达到最大，此时出现正向最大峰值加速度(C点)；当结构再次回弹到最高点时，在所模拟的倒塌荷载(悬挂在框架梁上的钢配重)和结构恢复力的共同作用下结构的加速度出现最大的负向峰值(D点)。此后，在阻尼作用下结构的振动逐渐衰减并最终停止。

图8 加速度时程曲线示意图

试件CB1和CB2失效柱位置的加速度峰值如表3所示。

表3 试件的峰值加速度

分析表3所示结果可知：

对于正向加速度，在30 kN和60 kN配重下，CB2的最大正向加速度分别约为CB1的1.96倍和1.08倍。正向加速度峰值大小与对应的结构恢复力密切相关。影响结构恢复力的因素包括结构刚度、框架梁偏离平衡位置的最大位移等。由表2可知，在30 kN配重作用下试件CB1和CB2的静态位移相差不大，但CB2所受的冲击效应明显增加，由此引起的动态位移响应明显大于CB1；当失效柱处达到最大动态位移时，试件CB2产生的结构恢复力将大于CB1，并导致正向加速度明显增加。而在60 kN配重作用下2个试件所受的冲击效应接近，这与配重的制振作用有关。

对于负向加速度，当结构振动至最高点时，在结构自重、结构恢复力及钢配重的共同作用下，结构将产生较大的负向加速度。根据表3可知，在30 kN和60 kN的配重作用下，CB2的负向加速度分别为CB1的2.68和1.15倍。

综上，组合框架梁中的预制混凝土板分段会导致倒塌荷载对结构动力冲击效应的增大；60 kN倒塌荷载对应的冲击效应系数小于30 kN倒塌荷载对应的系数。

3.3 钢梁动态应变响应

在图1中截面1—1和2—2的钢梁上、下翼缘各布置一个应变测点，实测的应变时程曲线分别如图9所示。

(a)CB- 1(截面1—1)

利用钢梁上下翼缘的应变差除以钢梁高度可以得到钢梁的截面曲率。在30 kN和60 kN配重下，两个截面中钢梁的截面曲率如下：①在截面1—1处，CB1的钢梁截面曲率分别为2.3×10-6/mm和5.1×10-6/mm，CB2的钢梁截面曲率分别为1.8×10-6/mm和3.2×10-6/mm；②在截面2—2处，CB1的钢梁截面曲率分别为1.9×10-6/mm和3.8×10-6/mm，CB2的钢梁截面曲率分别为2.0×10-6/mm和6.0×10-6/mm。钢梁曲率的变化与以下因素有关：①由于CB2中预制板不连续，子结构在预制板拼缝处产生了刚度突变，结构传力模式的变化导致截面1—1内钢梁截面曲率的变化；②CB2在截面2—2处的钢梁截面曲率明显大于试件CB1，说明预制板分段后截面2—2处的钢梁承担了相对较多的截面弯矩。

2个试件的钢梁应变响应如表4所示，其中εd，max为最大动态应变响应，εs为静止后钢梁应变，βε=εd，max/εs为钢梁应变增大系数。

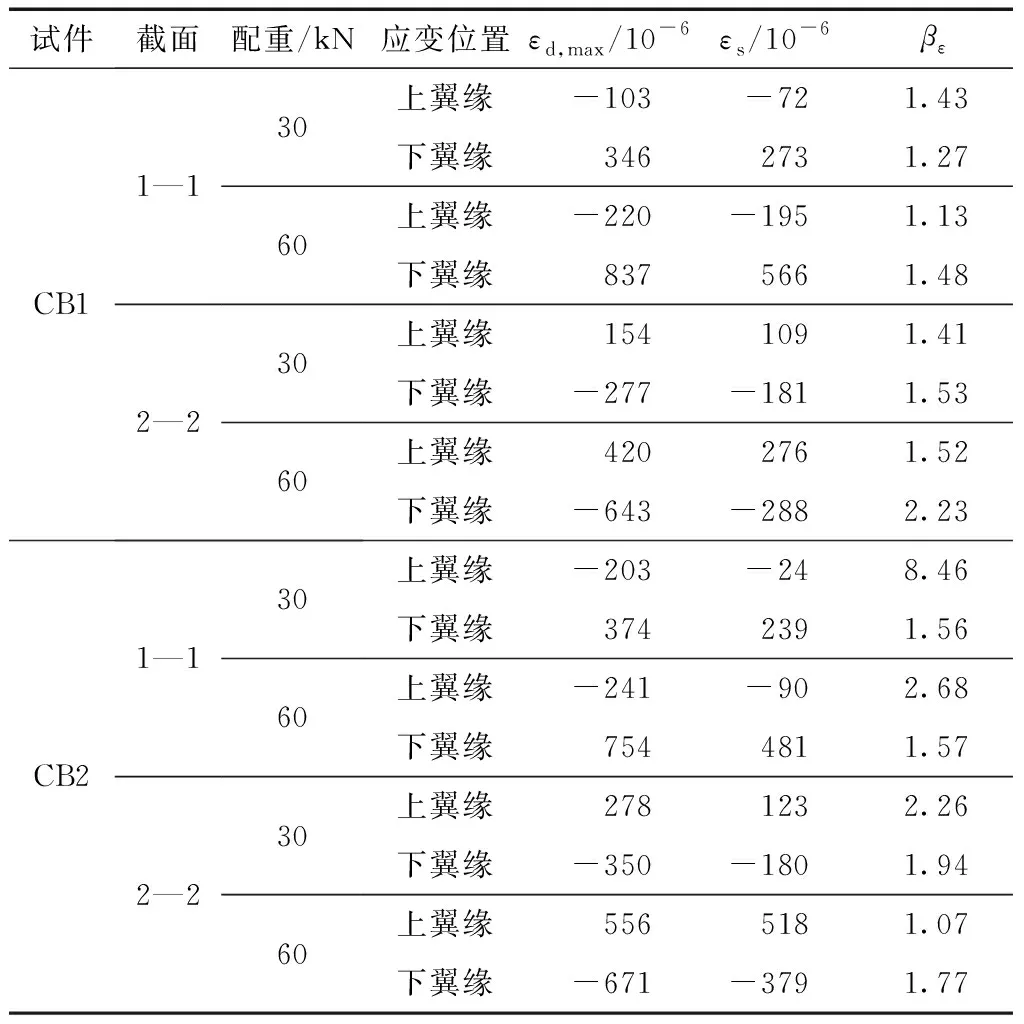
表4 钢梁端部应变响应

由表4可知，在30 kN和60 kN配重下，试件CB2在梁端截面1—1内钢梁上、下翼缘的应变增大系数均大于CB1；在靠近边柱的梁端截面2—2内钢梁上、下翼缘的应变增大系数在多数情况下大于CB1。此外，两个试件钢梁上、下翼缘处的测点应变增大系数均出现了大于2.0的情况，这与混凝土板开裂或焊缝受损而引起的局部应力变化有关。由此可知，在静力倒塌分析过程中如果忽视局部结构损伤的影响，所得分析结果可能无法全面反映结构构件在倒塌荷载冲击作用下的动态应变。

3.4 钢筋动态应变响应

在框架梁截面1—1和2—2混凝土板的纵向钢筋上布置应变测点，如图2所示。失效柱附近的钢筋由于承受正弯矩作用始终处于受压状态，边柱附近钢筋由于承受负弯矩作用始终处于受拉状态。

表5 钢筋应变响应

通过对两个试件βεr进行对比可知，试件CB1和CB2的钢筋应变增大系数最大值分别为2.37和2.85。在多数情况下，试件CB2的钢筋应变增大系数均高于试件CB1，说明混凝土板分段会使得梁端混凝土板中纵向钢筋承受更大的冲击效应。这是由于在预制混凝土板分段后，相同大小的倒塌荷载引起的冲击作用增大，进而导致梁端钢筋应变增加。

3.5 结构的动力特性

在抽柱前后通过敲击法分别测得两个试件在中柱失效前后结构的动力特性，试件CB1和CB2在两种配重下抽柱前后的基频(f)与阻尼比(ξ)如表6所示。

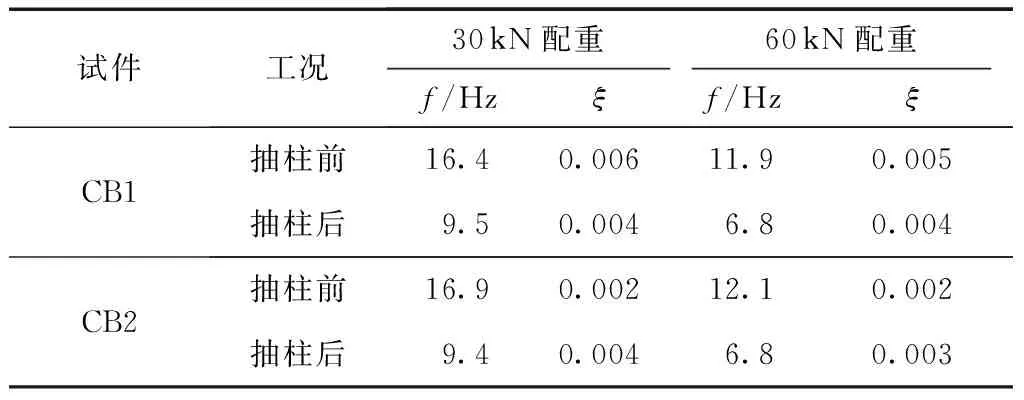
表6 试件基频与阻尼比

从表6中可以看出，抽柱后结构基频变为抽柱前的一半左右。抽柱前CB1在30 kN和60 kN配重下的阻尼比均高于CB2，意味着CB2在倒塌过程中能量耗散相对CB1更慢，从而导致振动时间更长，这与失效柱位移时程曲线表现出的规律相一致。

4 倒塌荷载动力增大系数DIF

文献[21]探讨了以栓钉及开孔板为抗剪连接件的现浇式组合框架的动态倒塌性能。本研究试验所得到的失效柱的位移增大系数βΔ、钢梁应变增大系数βε和梁端板中钢筋应变增大系数βεr以及文献[21]中的相关结果如表7所示，其中本研究试验所得的βε和βεr分别以截面1—1钢梁下翼缘和截面2—2板中钢筋为研究对象。对比可知，与文献[21]中现浇混凝土组合梁相比，采用装配式组合梁之后，试件在相同倒塌荷载下的倒塌响应(如位移、应变等)增大系数均有不同程度的增加，这说明采用预制装配的结构形式及预制板分段均会导致组合框架倒塌响应动力增大参数变大。

表7 结构倒塌响应的增大系数

根据前文所完成的动力倒塌试验分析可知，子结构的损伤有限，剩余结构仍具有较好的承载能力。因此，在抽柱试验结束后，卸去框架梁上的钢配重，对中柱施加连续静力荷载直至试件最终倒塌破坏。最终破坏时，试件CB1边柱与钢梁上翼缘焊缝首先开裂，然后裂缝延伸至钢梁腹板并导致结构承载力显著下降；试件CB2靠近中柱梁端混凝土先压碎，随后靠近边柱的梁端混凝土剥落，与边柱相连的钢梁上翼缘在第一排螺栓孔处开裂，最终导致试件破坏。静力倒塌试验得到2个试件的荷载-失效柱竖向位移曲线如图10所示。

图10 荷载-竖向位移曲线

参照文献[21]的方法得到倒塌荷载等效动力增大系数DIF曲线，如图11所示。由图可知，DIF曲线呈现3阶段的变化规律：①在倒塌的初始阶段，倒塌荷载的动力增大系数随位移增加而快速增大至2.0左右；②DIF在接近2.0后开始随着位移的增加而逐渐减小并最终趋近于1.0；③在达到最低点后，DIF又随中柱竖向位移的增加开始增大。将图11中的横坐标进行无量纲化处理，通过数据拟合得到对装配式组合框架进行倒塌分析时倒塌荷载DIF的简化数学模型：

(1)

式中，Δ为倒塌过程中失效柱竖向位移，l为结构跨度。

需要说明的是，参照CB2破坏时中柱竖向位移与梁跨度的比值，最终确定式(1)中挠跨比Δ/l的截止上限值为0.143。

图11 DIF与竖向位移关系曲线

文中简化计算模型与文献[21]中计算模型的对比如图12所示。

对比图12可以看出，DIF达到最低点前，相同位移下现浇式组合框架的DIF取值大于装配式组合框架；在结构进入悬链线效应阶段后，当具有相同挠跨比Δ/l时，两者的DIF取值几乎相同。将本研究中不同配重下抽柱后失效柱的静止位移代入文中式(1)，得到30 kN和60 kN倒塌荷载对应的等效动力增大系数DIF值为1.98和1.95。与表7所示的结构倒塌响应的动力增大系数相比，在柱失效后如果剩余结构仍处于弹性工作状态，倒塌荷载等效动力增大系数DIF的理论计算值在多数情况下都偏于保守。

图12 DIF简化数学计算模型对比

5 结论

通过对采用预制混凝土板的装配式组合梁框架子结构开展动态倒塌试验，得到以下结论：

(1)在1倍倒塌荷载(30 kN)和2倍倒塌荷载(60 kN)的作用下，装配式钢-混凝土组合框架子结构的主要损伤为靠近边柱的框架梁端混凝土板的开裂，并在板顶预留螺栓孔两侧边形成沿梁跨度方向的贯通裂缝；中柱失效后，剩余结构仍具有较好的承载能力和整体刚度，剩余子结构不会发生连续倒塌破坏。

(2)预制板分段后子结构振动时长增加，但对结构频率、阻尼等动力特性的影响较为有限；预制板分段后，30 kN倒塌荷载对结构的冲击效应最为显著，60 kN倒塌荷载对结构的冲击效应变化不大。

(3)与现浇混凝土组合梁相比，装配式组合梁框架承受的倒塌荷载冲击效应更大；在预制板分段后，中柱位移动力增大系数介于1.38～1.65之间，梁端钢梁应变和预制混凝土板中钢筋应变的增大系数通常会增大；在部分情况下，应变增大系数会出现大于2.0的情况。

(4)基于试验结果建立的中柱失效情况下装配式组合框架倒塌荷载动力增大系数DIF的数学计算模型，可为开展此类结构静力倒塌分析时倒塌荷载的修正提供参考；与实测的结构倒塌响应(如：应变、位移等)的动力增大系数相比，基于所提出数学模型得到的倒塌荷载DIF计算值偏于保守。