快速路合流区大型车换道时空特征及风险研究

温惠英 李秋灵 赵胜

(华南理工大学 土木与交通学院，广东 广州 510640)

随着客货运量的不断增长，大型车在道路运输中的车型占比逐年增加，对道路交通运行产生较大影响。与小轿车相比，大型车在车辆尺寸、动力性能和事故特征方面呈现明显差异。由于大型车长度与宽度比小轿车更大，占据横纵向空间多，其换道和转向所需的空间大、持续时间长，对周围驾驶人产生强烈的压迫感。同时，大型车较高，易遮挡后方车辆和两侧车辆的视线，严重影响周边其他车辆视距，是交通事故的重要致因。在动力性能上，大型车的最高车速、最大爬坡坡度和操纵稳定性均低于小轿车；且因其质量大，运动惯性与动能庞大，故制动时间比小轿车长。在事故特征上，大型车发生重特大交通事故的可能性更大。据统计，当事故中有中大型车时，发生重特大事故的数量占总事故数的比例为74.30%；而当事故中没有中大型车时，发生重特大事故的数量占总事故数的比例为48.03%[1]。鉴于大型车在道路交通运输上的重要地位及其对交通安全的深远影响，有必要深入研究大型车驾驶行为与行车风险特征。

跟驰与换道是快速路上两种典型的驾驶行为。与跟驰行为相比，大型车变换车道时，驾驶员不仅需频繁观察当前车道前后车的位置与速度，还应时刻注意其与目标车道前后车的间距，精神与心理负荷较大，易诱发错误决策或失误操作。同时，由于车辆尺寸与动力性能上的异质性，大型车换道行为的影响范围广、持续时间长，对局部交通流的扰动明显，更容易发生交通冲突，甚至引起交通事故。因此，文中着重研究大型车的换道行为特性，挖掘其时空风险分布规律。

国内外学者围绕换道行为开展了诸多研究并取得了大量的成果，现有研究主要集中在换道特性分析和换道安全性分析上。在换道特性分析方面，已有较多的研究分析了小轿车换道行为的时空特征，主要包括换道持续时间、纵向换道行驶距离、换道车辆与周围车辆状况等。Olsen等[2]研究发现小轿车平均换道时间为6.28 s，且超过37%的换道致因来自前方慢车。党睿娜等[3]发现70%的驾驶员在接近前车时选择换道，且换道时的加速度为-1～1 m/s2。Wang等[4]研究得出车辆速度为15～20 m/s时，其向左换道与向右换道时长没有显著区别。王雪松等[5]通过分析车辆运动轨迹数据发现，换道切入的平均持续时间为3.82 s，且约有15%的驾驶员在前车变道切入时速度变化超过10%，表现出明显的“不礼让”。王畅等[6]研究发现营运客车平均换道持续时间为10.4 s，且车速越高，横向偏移量越小，换道轨迹与车道线夹角也越小。Yang等[7]采用多级混合效应模型，分析了换道间隙及换道持续时长与影响因素之间的关系。马小龙等[8]研究发现，平均换道时间为6.09 s、平均换道距离为148.08 m，换道车辆与目标车道后车的平均距离最小，与正前方车辆的平均速度差最大。此外，部分学者对不同气候条件[9]、交通环境[10]、交通状态[11]下的换道行为特性进行了研究；同时，驾驶人特征[12- 13]和驾驶设备[14]对换道行为的影响也广受研究者的关注。在换道安全性分析方面，已有研究证明车辆换道行为影响道路交通流状态[15]，可能降低道路交通容量[16]。Oh等[17]采用二元逻辑回归模型对车辆换道行为进行仿真，计算车辆与前车之间的TTC(碰撞时间，Time to Collision)，得到碰撞概率，并基于此描述相邻车辆间的碰撞风险。Ali等[18]建立了持续生存模型，用于量化车联网环境对强制换道安全性的影响。张兰芳等[19]基于比例优势模型，分析了高速公路出口区换道风险分布特征。彭涛等[20]基于侧向速度正态分布拟合方法，建立了考虑人-车-路相互作用的高速公路弯道路段车辆紧急避撞安全换道模型。柳本民等[21]通过分析影响换道越线时间的各项因素，建立了越线时间Cox比例风险模型。薛清文等[22]利用修正碰撞裕度对跟驰和换道行为进行风险评估，以识别危险驾驶行为。Wu等[23]用TTC、SDI(停车距离，Stopping Distance Index)两个指标分别衡量时间、空间风险水平，通过故障树分析法构建综合风险指数，实时识别换道风险。Chen等[24]划分了16种不同换道模式，在考虑影响换道安全因素异质性的基础上进行风险评价。

综上，国内外在换道特性和安全性等方面的研究已取得了大量的成果，但存在研究的车辆类型比较单一、研究内容较少考虑时空关系等问题。一方面研究对象多为小轿车，而大型车与小轿车在车辆尺寸、动力性能和事故特征等方面都存在差异，因此有必要研究其不同的换道特性。另一方面，大型车换道安全性与周围车辆的运行工况存在复杂的时空关系；例如，大型车与周围车辆之间的TTC越小，其安全性越低等；大型车在前车速度较慢或跟驰间隙较小时倾向于换道，且在换道过程中与各邻近车辆之间的安全交互关系存在差异。因此，有必要研究大型车换道的时空特征及其安全性，挖掘大型车换道时的潜在危险源，为大型车交通事故预防与识别提供参考依据。有鉴于此，文中基于快速路合流区大型车运动轨迹数据，分析合流区大型车换道时空特性和安全风险；以期为大型车换道决策模型和换道辅助系统的建立，以及对快速路合流区交通安全优化等提供借鉴和指导。

1 数据来源及处理

1.1 数据来源

文中数据来源于东南大学智能交通实验室分享的开源数据集[25]，该数据集采自中国江苏省南京市龙蟠南路快速路高架合流区(图1中的红色方框内区域)。合流区路段长度为427 m，由东向西合流，东端为单向5车道，西端为单向3车道。研究团队借助无人机(大疆“御”Mavic Pro)在310 m高空连续拍摄4 min15 s，运用图像识别技术提取车辆运动轨迹数据，帧率为24帧/s，经过人工校核确保数据实现100%车辆识别跟踪，得到每辆车的位置坐标、速度、加速度、车道等信息。

图1 无人机拍摄的合流区路段

1.2 数据处理

在换道过程中，大型车与周围车辆频繁博弈，其交互对象最多涉及4辆车，即原车道和目标车道的前后车。记换道车辆为O、原车道前车为F1、原车道后车为B1、目标车道前车为F2、目标车道后车为B2，如图2。本研究将车身长度超过6 m的车辆定义为大型车，设大型车所在车道编号变化的时刻为其换道瞬间(设为第n帧)，截取换道瞬间前108帧和换道瞬间后107帧数据(时间长度为9 s)，并截取原车道和目标车道前后车对应时间段的216帧数据，共同构建大型车换道样本，如图3所示。经过数据处理，剔除不完整或异常的数据，获得191个大型车换道样本。

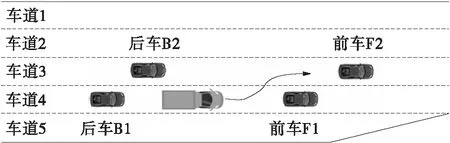
图2 换道车辆与周围车辆关系

图3 换道样本

为了分析大型车换道特征，有必要确定样本中的换道起点与终点。对于换道起点和终点的识别，已有学者提出诸多方法，但尚未形成统一标准。党睿娜、王忠宇等[3，10]以车辆与车道线之间的相对距离为标准，对换道行为起终点进行判断，而马小龙等[8]则以换道车辆是否持续横向偏移为判断依据。文中结合前人研究成果，选取车辆开始持续横向偏移的时刻作为换道起点，结束持续横向偏移的时刻为换道终点。如图4所示，换道车辆从A时刻开始向目标车道持续偏移，在B时刻车辆中心点跨越车道线，到C时刻结束。设换道起始时刻A至结束时刻C之间的时间间隔为换道持续时间tc；车辆在换道过程中的纵向行驶距离为Lc。文中以B时刻为分界线，将车辆换道过程分为两部分：车辆开始换道至恰好跨越车道线的时间间隔设为前半时间t前；车辆越过车道线至换道结束的时间间隔设为后半时间t后。

图4 车辆换道轨迹

2 大型车换道时空特性分析

2.1 换道时间分析

2.1.1 换道持续时间tc

通过统计大型车换道持续时间tc，发现其均值为5.28 s，最小值为1.96 s，最大值为8.97 s，标准差为1.78，且45.03%的大型车换道持续时间集中在4～6 s之间。由于研究场景为快速路合流区，强制换道现象较多，样本中大型车换道持续时间的均值略小于马小龙等[8]和王畅等[6]的研究结果。

在车辆换道时间分布上，王雪松等[5]选取8种分布类型对变道切入持续时间进行拟合，发现Lognormal分布拟合效果最好。为了分析大型车的换道时间分布规律，本研究选取Normal、Lognormal、Logistic、Log-Logistic、Gamma和Weibull 6种模型对换道持续时间分布情况进行拟合，计算各模型的赤池信息量准则(Akaike Information Criterion，AIC)，其中AIC越小说明拟合效果越好，如表1和图5所示。结果显示，用Weibull分布模型拟合大型车换道持续时间的效果最佳，其密度函数为

(1)

式中，x为随机变量，λ为比例参数，k为形状参数。

表1 6种模型拟合效果对比

图5 换道持续时间频率分布

2.1.2 前半时间t前与后半时间t后

经统计，大型车换道前半时间t前的均值为2.60 s，标准差为1.19；后半时间t后的均值为2.68 s，标准差为1.05。同样选取上述6种数学模型分别对t前和t后进行分布拟合，发现采用Weibull分布拟合效果最佳，如表1和图6-图7所示。

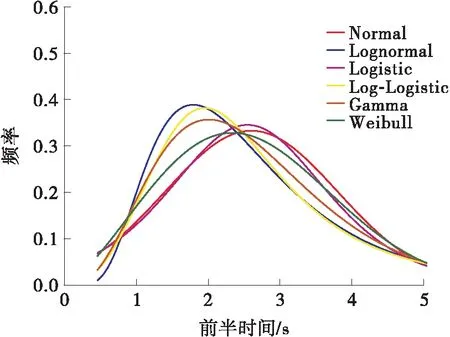
图6 前半时间频率分布

图7 后半时间频率分布

2.2 换道空间分析

2.2.1 换道位置分布

由于快速路合流区外侧车道合并形成瓶颈区域，大型车换道位置在横向与纵向分布上均呈现鲜明的特点。在横向上，大型车在不同车道的换道方向与频数存在显著差异。设车道编号由内向外依次增加，最内侧车道为车道1，最外侧车道为车道5，则大型车在各车道的换道情况如表2所示。由表2可见，除车道1外，大型车在其他车道向左换道的次数均比向右换道多，且车道3、4、5均为向左换道。这主要是因为大型车在车道1上只能向右换道，而车道5和车道4先后并入内侧道路，大型车被迫向左换道，并诱发车道2和车道3上的大型车逐渐向左换道以获取更大行驶空间。

表2 各车道的大型车换道分布情况

在纵向上，车辆换道位置与距离合流区瓶颈路段的剩余长度有关。文中设车道横断面为横向，根据车道数划分为5个部分，车辆行进方向为纵向，根据换道位置分布情况划分为18个部分，由此得到5×18个方格，每个方格规格为3.5 m×20 m，统计各方格内的大型车换道数，绘制热力图如图8所示。

图8 各车道换道热力图

由图8可知，大型车在车道5的换道位置集中在沿车道线距离处于区间[40，140)的路段(即距离合流区瓶颈1起点前84 m至起点后16 m)，其中在区间[100，120)上换道的车辆数最多(即距离合流区瓶颈1起点前4～24 m)；大型车在车道4的换道位置主要分布在区间[100，240)上(即距离合流区瓶颈2起点前23～163 m处)，呈现两区域集聚现象，即大型车在区间[100，140)(即距离合流区瓶颈2起点前123～163 m)和[160，240)(即距离合流区瓶颈2起点23～103 m处)上换道频繁；车道5上的车流受合流区瓶颈1的道路条件约束，强制换道至车道4，故大型车在车道4上的区间[100，140)内的换道行为更加密集；车道4与车道3的合并则造成大型车在车道4上的区间[160，240)内换道频繁；大型车在车道3上的换道位置分布较广，主要集中在区间[100，160)上(即距离合流区瓶颈2起点103～163 m处)；大型车在车道2上的换道位置分布相对均匀，在车道1上的换道行为较为稀疏。

整体上，75.40%的大型车换道行为集中于瓶颈处前100 m内，且呈现向内侧车道扩散趋势。例如：车道5上的车辆换道至车道4后，车道4和车道3上的车辆随之向左换道，以获取更高的行驶速度。相对而言，大型车在车道2和车道1上的换道次数较少，这主要是因为内侧车道为快车道，多为小轿车行驶，而大型车倾向于在外侧车道行驶。

2.2.2 纵向换道行驶距离Lc

根据统计结果，大型车的纵向换道行驶距离Lc的均值为78.12 m，标准差为27.03。选取6种模型对Lc进行拟合，结果表明Weibull分布拟合效果最佳，见表1和图9。

图9 纵向换道行驶距离频率分布图

2.2.3 换道间距di

换道车辆与周围车辆i(即F1，B1，F2，B2)之间的距离是决定驾驶员是否执行换道和换道风险高低的重要评判标准，若间距过小，则无法保障车辆在换道过程的安全性。大型车在换道瞬间与周围车辆的间距di分布规律如图10所示。

图10 换道车辆与周围车辆间距

大型车在换道瞬间与周围车辆F1、B1、F2、B2的间距均值分别为22.91、38.31、30.42和28.94 m。其中，大型车与原车道前车F1的间距最小，分布最密集，这主要是驾驶员通常会因与前车距离过小而采取换道行为，以追求更舒适的行车体验。此外，大型车与目标车道后车B2的间距也较小，分布较为密集，这主要是因为大型车在换道前更加关注其与目标车道后车B2的间距，若两者间距较小，则其换道碰撞风险较高，此时驾驶员倾向于选择等待下一个换道时机。大型车与原车道后车B1的距离分布最为分散，表明原车道后车B1对大型车换道行为的影响较小。

2.2.4 换道速度差ΔVi

换道车辆与周围车辆i之间的相对速度差ΔVi是影响换道安全性的重要指标，设ΔVi为

ΔVi=Vi-VO

(2)

式中：i为周围车辆编号(即F1，B1，F2，B2)；Vi为车辆i的速度，m/s；VO为换道车辆O的速度，m/s。

经统计，大型车与周围车辆的速度差ΔVi如图11所示。大型车与周围车辆F1、B1、F2、B2的速度差均值分别为-0.90、0.26、0.17和-0.26 m/s，其中大型车与目标车道后车B2的速度差波动较大、异常值最多；大型车与原车道后车B1和目标车道前车F2的速度差均值为正，表明大型车与原车道后车B1发生碰撞的可能性较大，而与目标车道前车F2发生碰撞的可能性较小；大型车与原车道前车F1的速度差均值最小，表明大型车换道的主要原因是前方有慢车，与Olsen等[2]的研究结论一致；大型车与目标车道后车B2的速度差均值为负，这可能是由大型车加速换道或目标车道后车主动避让大型车引起的。

图11 换道车辆与周围车辆速度差

2.2.5 目标车道换道间隙ΔS及其变化速率ΔVs

驾驶员在换道时通常综合考虑目标车道换道间隙及其演变趋势，以决定是否换道。文中采用目标车道前车与后车的速度差ΔVs描述换道间隙的变化速率，并输出大型车换道时的换道间隙ΔS与速度差ΔVs之间的关系，如图12所示。

由图12可见，当ΔS>50 m时，ΔVs的分布比较离散，这说明在换道间隙足够大时，换道间隙变化速率不是影响驾驶员是否换道的决定性因素；当ΔS≤50 m时，ΔVs明显集中在区间[-1，5)上，这说明在换道间隙较小时，驾驶员更倾向于选择在换道间隙缩小缓慢或不断扩大的情况下换道。

图12 目标车道换道间隙与其变化速率的关系

2.3 大型车时空特征相关性分析

运用SPSS软件，研究换道持续时间tc、前半时间t前、后半时间t后、纵向换道行驶距离Lc与大型车换道起止车道、速度、加速度、沿车道线距离、换道间距di、换道速度差ΔVi之间的相关性。经Pearson检验后，得到结果如表3所示。

由表3可知，换道持续时间tc与速度、换道间距dF1、换道间距dF2在1%的显著性水平上显著相关，与沿车道线距离、换道速度差ΔVF1、换道速度差ΔVB1在5%的显著性水平上显著相关；前半时间t前与速度、沿车道线距离、换道间距dF1、换道间距dF2在1%的显著性水平上显著相关，与换道速度差ΔVB1在5%的显著性水平上显著相关；后半时间t后与速度在1%的显著性水平上显著相关；换道行驶距离Lc与速度在1%的显著性水平上显著相关，与换道间距dB1在5%的显著性水平上显著相关。

表3 大型车换道时空特征相关性分析

3 大型车时空风险分析

常见的交通安全评价指标有碰撞时间TTC、碰撞余量MTC(Margin to Collision)和停车距离SDI等。TTC从时间层面刻画了车辆间发生碰撞的潜在风险，而MTC和SDI从空间层面描述了车辆间的行车风险。

3.1 时间风险分析

TTC是指两辆车以当前速度匀速行驶时距离碰撞的剩余时间(记为t)，大型车与周围车辆i之间的TTC为

(3)

式中：Δd为前车与后车的距离，m；VB为后车速度，m/s，VF为前车速度，m/s。

当后车速度小于或等于前车时，TTC为无穷大，两者之间不会发生碰撞；当TTC较大时，后车速度略大于前车或前后车间距较大，发生碰撞的可能性较小；当TTC较小时，后车速度大于前车或前后车间距较小，发生碰撞的可能性大。因此，文中选取TTC在区间[0，20]上的分布情况进行分析，如图13。

由图13可知，tF1的均值最小(8.66 s)，在区间[0，10)上的占比最大(62.90%)，有30.65%小于5.5 s，表明大型车与原车道前车F1发生碰撞的可能性最大，行车风险最高。这主要是因为大型车换道时与前车的间距较小，且速度差较大。tB1的平均值最大(11.06 s)，且分布最离散，表明大型车与原车道后车B1发生碰撞的可能性较小。这主要是因为大型车换道时与后车B1的间距较大且分布离散。

(a)TTC折线图

3.2 空间风险分析

MTC是前车减速至停车行驶的距离加前后车初始间距，与后车从反应到减速至停车行驶的距离的比值(记为p)，其计算公式为

(4)

式中：a为减速度，取6.86 m/s2[26]；tr为驾驶员反应时间，在紧急情况下取1.5 s[8]。

若MTC小于1，表明两车存在发生碰撞的可能性，且碰撞严重性随MTC减小而增大。大型车与周围车辆之间的MTC在[0，1)上的分布情况如表4所示。

表4 换道车辆与周围车辆的MTC分布情况

由表4可见，整体上，约有94%的MTC大于0.5。其中pB1和pF2在[0.7，1.0)上的占比分别为79.03%及79.76%，表明大型车与原车道后车B1、目标车道前车F2之间发生碰撞的严重程度不高。这主要是因为大型车与车辆B1、F2的速度差较小，且车间距较大。在区间[0.2，0.4)上pF1的占比最高，即5.00%，表明大型车与原车道前车F1发生碰撞的严重程度最高。

3.3 综合时空风险分析

为了深入挖掘大型车在换道过程中其时间风险与空间风险之间的内在联系，文中联合分析TTC和MTC的分布规律，当TTC的取值在[0，50]上时，TTC与MTC的关系如图14所示。

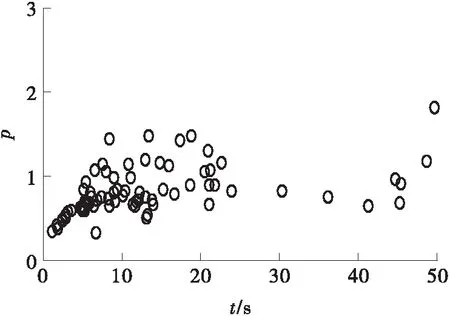
(a)原车道前车F1

从总体上看，TTC和MTC分别在区间[0，10]和[0，1]上分布集中，且MTC随TTC的增大而增大。原车道前车F1与大型车的TTC位于区间[0，5]上的样本较多，MTC多小于1，表明前车F1与大型车发生碰撞的可能性最高。原车道后车B1与大型车的TTC和MTC分布比较离散。目标车道前车F2和后车B2的分布规律相似，TTC在区间[0，15]上分布比较集中，但后车B2的TTC和MTC均接近0的样本数多于前车F2，这说明后车B2有更可能与大型车发生严重碰撞。

由前文可知，前后车发生碰撞的可能性随TTC的减小而增大，当MTC小于1时，前后车发生碰撞的严重性随MTC减小而增大。基于Olsen等对换道危险程度的分类[2]，文中设定当0

4 结论与展望

文中针对快速路合流区交通运行特性，获取南京市龙蟠南路快速路合流区的车辆运动轨迹数据，筛选并构建大型车换道样本，通过深入研究大型车换道特征及其时空风险，得出如下结论：

(1)大型车的换道持续时间、前半时间、后半时间和纵向换道行驶距离分布规律均服从Weibull分布模型。

(2)75.40%的大型车换道行为主要集中在合流区瓶颈路段前100 m内，呈现由外向内逐渐扩散的趋势，且在内侧车道分布较少；同时，大型车与原车道前车的速度差最大、车间距均值最小且分布最稳定；若目标车道换道间隙较小，多数大型车倾向于在换道间隙缩小趋势缓慢或不断扩大情况下变换车道。

(3)在1%的显著性水平下，大型车的换道持续时间和速度、与原车道前车间距、与目标车道前车间距显著相关；前半时间和速度、沿车道线距离、与原车道前车间距、与目标车道前车间距显著相关；后半时间与纵向换道行驶距离均和速度显著相关。

(4)大型车与周围车辆之间的MTC随TTC的增大而增大，且在换道时与原车道前车发生碰撞的可能性最大、严重程度最高，二者间换道安全交互失效的比例为15.32%。

文中研究结果可为大型车换道行为建模和换道辅助系统提供理论依据，有助于城市交通管理者制定或优化快速路合流区的交通管理措施。本团队未来拟通过无人机拍摄视频采集更多数据，研究不同交通环境下大型车换道风险识别与安全预警方法，减少大型车发生交通事故的可能性。