规定性知识:从“有意思”走向“有深度”
——《用数对确定位置》教学
文|张 程
【教学背景】
《用数对确定位置》是苏教版小学数学四年级下册第八单元的教学内容。数对属于规定性知识,如何将这节课上得既有意思,又有深度?备课前,我时常思考以下三个问题:如何引发学生的学习需求?规定性的知识值得探究吗?练习的设计应当关注什么?随着数次磨课,笔者对这三个问题的思考也更加深入。本文以《用数对确定位置》一课为例,就小学数学规定性知识如何教学作简要阐述。
【教学过程】
●思考1:如何引发学生的学习需求?
初次试教:知识本位,重关联。
师:五人排队买票,小军(见图1)排在第几个?

图1
生:小军排在第二个。
师:我们在排队时,如果只有一队,只要一个数就能确定一个点的位置。如果有很多队,又该怎么办呢?这节课我们进一步学习确定位置。
研磨修改:学生本位,重生成。
师:学校即将召开家长会,规定每个家长必须坐在自己孩子的座位上。如果你是小军(见图2),你打算怎样告诉爸爸妈妈你在教室里的位置?和你的组员交流你的想法。

图2
生:小军坐在第4组第3个。
生:小军坐在第3排第4个。
生:小军坐在第4列第3行。
师:小军的位置是固定不变的,但同学们在描述时却出现了多种说法。为什么同一人的位置却有不同的说法?看来,描述的标准不一致,就容易造成混乱。因此,我们需要用统一的标准来确定位置。
●思考2:规定性的知识值得探究吗?
初次试教:活动为主,重探究。
师:通常我们把竖排叫作列,确定第几列,要从观察者(老师)的左边数起,从左往右数。把横排叫作行,确定第几行,要从前往后数。我们一般先说列,再说行。
师:认识列和行了吗?谁能上来指一指?还有吗?
师:现在你能说说小军坐在第几列第几行吗?
生:小军坐在第4列第3行。
师:如果把每个学生的座位都用一个点表示,会得到这样一幅图(见图3)。想一想,小军的位置在哪里?用你喜欢的方式表示小军的位置,并和小组成员说说你是怎样想的。
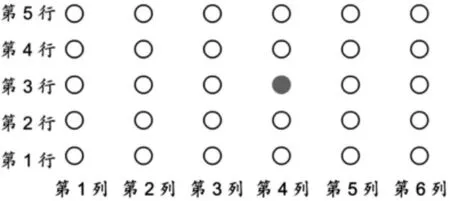
图3
生:第4列第3行。
生:43。
生:4、3。
生:4.3。
生:(4,3)。
师:你觉得哪种表示方法更好?为什么?
生:(4,3)比较好,和第4列第3行相比,更加简洁。
生:(4,3)比较好,因为43容易与整数43混淆,4、3和4.3容易与小数4.3混淆。
师:说来也巧,数学家也是这样表示的,这样一对特殊的数,在数学上叫作“数对”。在写数对时,我们一般先写列,再写行,用逗号隔开,最后用小括号把这两个数括起来。数对(4,3)读作:四三。
研磨修改:表达为主,重理解。
教师介绍列和行的含义。(同前文)
师:现在让我们将目光投向教室,如果从老师的视角来观察,第1列在哪里?请举手!第3行呢?请起立!那么你在教室里的位置是第几列第几行?
师:和你的同桌互相说一说。
师:让我们回到小军的班级,如果把每个学生的座位都用一个点来表示,会得到这样一幅图(见图3)。请你在图上标出每一列、每一行,并和你的同桌互相说一说。
师:你能在图上找到小军的位置吗?
师:小军坐在第4列第3行,可以用数对(4,3)表示。在写数对时,我们一般先写列、再写行,用逗号隔开,最后用小括号把这两个数括起来。
师:谁来给大家读一读?
生:四三。
师:数对中的4表示什么意思?3呢?
生:4表示第4列,3表示第3行。
●思考3:练习的设计应当关注什么?
初次试教:关注趣味,重体验。
1.火眼金睛。
师:小军班级还有其他同学,小芳和小刚又在哪里呢?看清楚就立刻将数对写在《学习单》上。
师:小伟的位置在(5,2),请你在图上涂色表示他的位置。
2.站!站!站!
师:现在让我们将目光投向教室,如果从老师的视角来观察,第1列在哪里?请起立!第3行呢?
师:你现在所在的位置用数对怎样表示?谁来说一说?
师:(4,1)、(4,2)、(4,3)这三个数对有什么共同点?猜猜老师接下来要请谁起立?(4,4)有什么特点?
师:(3,2)和(2,3)这两个数对,都用了2和3这两个数字,为什么站起来的同学却不同呢?你还能找一个和他们类似的数对吗?
师:看来,同学们不光清楚自己所在位置表示的数对,还能快速判断出其他同学对应的数对。那你能用数对介绍你的好朋友吗?你来描述,其他同学一起猜出他的名字。
师:接下来考验一下大家的反应能力。老师报一个数对,就请相应的同学起立,其他同学作出判断。准备好了吗?
师:为什么(4,■)、(▲,2)站起来这么多人?
师:(★,★)表示什么含义?
3.小小设计师。
师:这是小军班级为六一儿童节布置的盆花(见图4),你能用数对表示红花的位置吗?

图4
师:红花的位置有什么排列规律?
4.谁是幸运儿?
师:今天同学们的表现真不错,老师带了一些小奖品,想要奖励给大家,但数量有限,谁会是这个幸运儿呢?
线索1:数对中有个数字是4;线索2:(■,4);线索3:■是最小的单数。
5.幸运大抽奖。
师:刚刚的游戏很多同学都觉得不公平,幸运儿是老师事先确定好的。接下来,我们来一个公平的游戏:幸运大抽奖。抽中数对,请相应的同学起立,如果答对问题,就可以获得奖品;如果答错,机会就要让给其他人啦!
6.解密。
师:很多同学意犹未尽,老师今天还带来一个密令,你们有信心解出来吗?密令一共有五个字,就藏在这几句诗(见图5)里,给大家 一 些 提 示:(1,3),(6,5),(1,1),(6,4),(2,6)。

图5
师:“我思故我在”,这是著名数学家笛卡尔的至理名言,张老师今天把这句话送给爱思考的你们。发明数对的数学家正是笛卡尔,让我们一起看看他的故事吧!
(故事略)
7.魔方中的数对。
师:这是一个魔方,涂色小正方体的位置该用几个数来表示呢?
师:同学们的心中已经有了答案,这个问题留给你们课后研究。
研磨修改:关注深度,重内涵。
1.火眼金睛。(同前)
2.教室里的数对。
师:你在教室里的位置用数对怎样表示?谁来说一说?
师:(4,4)有什么特点?(3,2)和(2,3)这两个数对,都用了2和3这两个数字,为什么站起来的同学却不同呢?
师:看来用数对确定位置还要注意列和行的顺序。
3.数对接龙。
师:老师发现,大家不光清楚自己所在位置表示的数对,还能快速判断出其他同学对应的数对。接下来我们一起玩个游戏:数对接龙。由一名同学报一个数对,对应的同学迅速起立,并报下一个数对,以此类推……
师:同学们说得好,站的同学反应快,配合默契,掌声送给他们!
4.生活中的数对。
师:生活中也有许多数对。这是小军家厨房贴的瓷砖(见图6),请你用数对表示4块装饰瓷砖的位置。

图6
师:你有什么发现?
师:表示同一列的数对第一个数相同,表示同一行的数对第二个数相同。
5.点将台。
师:接下来,考验一下大家的反应能力。老师报一个数对,就请相应的同学起立,其他同学作出判断。准备好了吗?
师:为什么(4,■)、(▲,2)站起来这么多人?
师:(★,★)表示什么含义?
6.找邻居。
师:小红在教室里的位置用数对表示是(2,3),你能用数对分别表示出她前后左右四名同学的位置吗?先自己写一写,再和你的小组成员进行交流。
生:我是结合平面图看的,小红的前面是(2,2),后面是(2,4),她的左面就是我们的右面,所以是(3,3),她的右面就是我们的左面,所以是(1,3)。
生:我是结合教室座位看的,(2,3)是小红,她的前面是(2,2),后面是(2,4),左面是(3,3),右面是(1,3)。
师:看来,我们下次遇到这样的问题可以借助教室里的座位来思考。
7.图形中的数对。
师:请你用数对表示点A、B、C的位置(见图7)。

图7
师:如果有一个点D,并且连接这四个点能得到一个平行四边形,你能画出这个平行四边形,并用数对表示点D吗?
师:同学们一共找到了三种情况。看来,我们要多思考,才会有更多的收获。

