小讲师教学法

陈思思

【摘要】随着教育改革的不断推进，传统教学模式已难以服务于新课程改革的目标，提升数学教学质量已成为教师面临的难题.“双减”政策背景下，数学教师更应注重实施减负增效的新模式，从而减轻学生学习负担，以提升学生的学习效率，对于初中数学学习，避开题海战术、克服学生的畏难心理、培养学生举一反三的能力是数学核心素养的必然要求，本文以“小讲师教学法”为例，通过对例题、练习题和复习题等的变式训练，改变问题的呈现方式，促使学生养成多角度、多侧面分析问题的习惯，以培养学生核心素养发展.

【关键词】“双减”政策;变式训练;减负增效

“双减”政策背景下，教师应秉持减负增效的教学理念，引导学生进行题后反思.数学题目千变万化，但核心的数学思想却只有分类讨论、数形结合、图形变换、方程思想等，抓住了数学思想方法，将会事半功倍. 其中，尤其要加强几何教学中基本图形的变式拓展研究，培养学生识图（从复杂图形中抽象出基本图形）的能力，加强基本图形、基本方法、基本结论的渗透、复习，帮助学生建立几何模型、构建数形思维.

1精选作业设计

本文根据2021年武汉市四月调考第23题进行了改编，当做作业，同学们在30分钟内陆续完成，在校内完成数学家庭作业的效率大大提升.

23.（本小题满分10分）

如图1，P是正方形ABCD边BC上一个动点，线段AE与AD关于直线AP对称，连接EB并延长交直线AP于点F，连接CF.

（1）若∠BAP=30°，求∠AFE的大小;

（2）若∠BAP=α，∠AFE的大小是否发生变化，并说明理由;

（3）连FD，求证∠CFD=45°;

2引导学生探究思考

同学们在做题过程中提出问题：如图2，推导得∠EFA=45°，根据对称性得∠DFA=∠EFA=45°，先证∠CFD=45°（后面直接用）.

3让学生上台讲解

第一问同学们很快就做出来了，信心满满解决第二问和第三问，同学们先后想出不同的方法，并一一上讲台解答展示，分享自己的方法和思路，下列仅以部分学生成果.

（1）方法归纳：出发角度一，关注同侧的Rt△DBF和Rt△DBC.

方法1

作GC⊥CF交DF于点G，

则△CFB≌△CGD（ASA），

?△GCF为等腰直角三角形，

?∠CFD=45°（如图3）.

方法2

取BD中点O，

则OD=OC=OF=OB，

所以D、C、F、B四点共圆，

所以∠CFD=∠CBD=45°（如图4）.

（2）方法归纳：出发角度二，关注“异侧的Rt△ACD和Rt△ACF”.

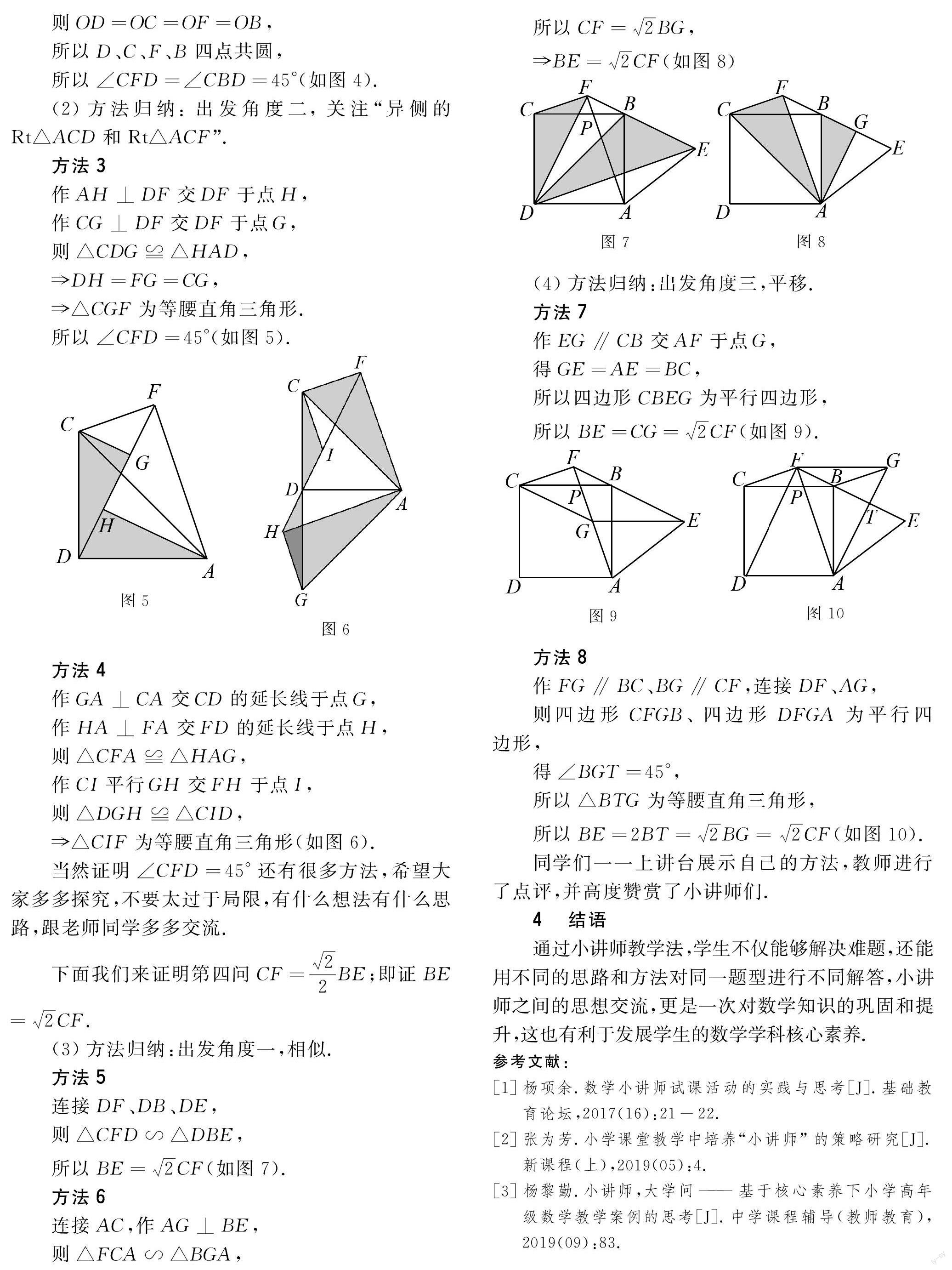
方法3

作AH⊥DF交DF于点H，

作CG⊥DF交DF于点G，

则△CDG≌△HAD，

?DH=FG=CG，

?△CGF为等腰直角三角形.

所以∠CFD=45°（如图5）.

方法4

作GA⊥CA交CD的延长线于点G，

作HA⊥FA交FD的延长线于点H，

则△CFA≌△HAG，

作CI平行GH交FH于点I，

则△DGH≌△CID，

?△CIF为等腰直角三角形（如图6）.

当然证明∠CFD=45°还有很多方法，希望大家多多探究，不要太过于局限，有什么想法有什么思路，跟老师同学多多交流.

（3）方法归纳：出发角度一，相似.

方法5

连接DF、DB、DE，

则△CFD∽△DBE，

方法6

连接AC，作AG⊥BE，

则△FCA∽△BGA，

（4）方法归纳：出发角度三，平移.

方法7

作EG∥CB交AF于点G，

得GE=AE=BC，

所以四边形CBEG为平行四边形，

方法8

作FG∥BC、BG∥CF，连接DF、AG，

则四边形CFGB、四边形DFGA为平行四边形，

得∠BGT=45°，

所以△BTG为等腰直角三角形，

同学们一一上讲台展示自己的方法，教师进行了点评，并高度赞赏了小讲师们.

4结语

通过小讲师教学法，学生不仅能够解决难题，还能用不同的思路和方法对同一题型进行不同解答，小讲师之间的思想交流，更是一次对数学知识的巩固和提升，这也有利于发展学生的数学学科核心素养.

参考文献：

[1]杨项余.数学小讲师试课活动的实践与思考[J].基础教育论坛，2017（16）：21-22.

[2]张为芳.小学课堂教学中培养“小讲师”的策略研究[J].新课程（上），2019（05）：4.

[3]杨黎勤.小讲师，大学问——基于核心素养下小学高年级数学教学案例的思考[J].中学课程辅导（教师教育），2019（09）：83.