N(2,2,0)代数的(λ,μ)-反犹豫模糊子代数
姜 曼
(西安交通工程学院 数学教研室,陕西 西安 710000)
文献[1]给出了一种新的(2,2,0)代数(S,*,Δ,0),并称其为N(2,2,0)代数. 文献[2]给出了N(2,2,0)代数子代数的概念,对于N(2,2,0)代数结构的研究,更多结论可参见文献[3-6]. 自1965年Zadeh提出了模糊集[7]后,模糊集理论被广泛应用于各个领域. 经过不断的发展和研究,模糊集在理论和应用两方面取得了很大的进展. 文献[8-10]将N(2,2,0)代数与模糊集相结合,研究了N(2,2,0)代数上不同类型的模糊子代数及相关性质. 2010年,Torra提出了犹豫模糊集[2]概念,犹豫模糊数比传统模糊元更全面,在多个数学模型中都有应用. 关于犹豫模糊集和代数系统的研究,可参见文献[11-14].论文把犹豫模糊集与N(2,2,0)相结合,提出了N(2,2,0)代数的(λ,μ)-反犹豫模糊子代数的概念,得到了若干个等价刻画,讨论了同态映射下N(2,2,0)代数的反犹豫模糊子代数的像与原像之间的关系,给出了犹豫模糊集下的反直积定义,研究了犹豫模糊反直积的相关性质,相关结果进一步完善了模糊代数和N(2,2,0)代数的理论研究.
1 预备知识
定义1[1]设S是有0元素的集合. 在S中定义两个二元运算*和Δ,若它们满足下列公理,即对∀x,y,z∈S,都有:
(1)x*(y*z)=z*(x*y);
(2) (xΔy)*z=y*(x*z);
(3) 0*x=x.
则称(S,*,Δ,0)是一个N(2,2,0)代数,简称S是一个N(2,2,0)代数.
论文约定S表示N(2,2,0)代数(S,*,Δ,0).
定义2[2]设Q是S的子集,若对∀x,y,z∈S,都有:①0∈Q;②由∀x,y∈S,可推出x*y∈Q,yΔx∈Q. 则称Q是S上的一个子代数.
引理[2]Q是S上的一个子代数当且仅当0∈Q且∀x,y∈S,x*y∈Q.
定义3[7]设A∈F(K)是一个非空经典集合,一个A∈F(K)上的犹豫模糊集A定义如下
A:{(x,hA(x))|x∈X},
其中:hA(x)是由区间[0,1]上若干个不同值构成的集合,表示A∈F(K)中的元素x属于集合A的若干种可能隶属度.
设A为A∈F(K)中的犹豫模糊集,P([0,1])为区间[0,1]的幂集. 称集合
K(A,γ):={x∈K|γ⊆hA(x)}
为A的犹豫水平集,其中:γ∈P([0,1]).
定义4[7]设X是一个非空经典集合,F和G是X上的犹豫模糊集,且具有如下形式
F:{(x,hF(x))|x∈X},G:{(x,hG(x))|x∈X}.
规定如下运算:
(1) 对于F,它的补元Fc定义为
补运算满足对合律,即(Fc)c=F.
(2)F和G的并F∪G定义为
hF∪G(x)=hF(x)∪hG(x)={h∈hF(x)∪hG(x)|h≥max(hF(x),hG(x))}.
(3)F和G的交F∩G定义为
hF∩G(x)=hF(x)∩hG(x)={h∈hF(x)∩hG(x)|h≤min(hF(x),hG(x))}.
定义5[14](反扩张原理) 设X,Y是两个集合,f:X→Y是一个映射.A和B是两个分别定义在X,Y的犹豫模糊子集.x∈X,∀y∈Y,定义Y的犹豫模糊子集f(A)为
∀x∈X,定义X的犹豫模糊子集f-1(y)为hf-1(B)(x)=hB(f(x)).
2 N(2,2,0)代数的(λ,μ)-反犹豫模糊子代数
定义6设A是S上的犹豫模糊子集,若∀x,y∈S,0≤λ<μ≤1,有:
(1)hA(0)∩μ⊆hA(x)∪λ;
(2)hA(x*y)∩μ⊆hA(x)∪hA(y)∪λ;
(3)hA(xΔy)∩μ⊆hA(x)∪hA(y)∪λ.
则称A是S的(λ,μ)-反犹豫模糊子代数.
注意到N(2,2,0)代数满足x*y=yΔx,从而定义6中的(2)和(3)等价. 故S上的犹豫模糊集A是(λ,μ)-反犹豫模糊子代数的充要条件是(1)和(2)成立,或者(1)和(3)成立.
定理1给出了N(2,2,0)代数的(λ,μ)-反犹豫模糊子代数与子代数的关系.
定理1设A是S的一个非空犹豫模糊子集,则A是S的(λ,μ)反犹豫模糊子代数,如果∀ε∈[λ,μ),L(A;ε):={hA(x)⊆ε|x∈L}(≠∅),则L(A;ε)是S的子代数.
证明∀ε∈[λ,μ),因为L(A;ε):={hA(x)⊆ε|x∈S}非空,所以存在x0∈L(A;ε),从而有hA(x0)⊆ε. 因为A是S的(λ,μ)反犹豫模糊子代数,从而∀x∈S,有hA(0)∩μ⊆hA(x)∪λ,因此有hA(0)∩μ⊆hA(x0)∪λ⊆ε∪λ=ε,又由于λ≤ε<μ,所以hA(0)⊆ε,即0∈L(A;ε). 另外,如果x∈L(A;ε),y∈L(A;ε),则hA(x)⊆ε,hA(y)⊆ε,且hA(x*y)∩μ⊆hA(x)∪hA(x)∪λ⊆ε∪ε∪λ=ε,这表明hA(x*y)⊆ε,即x*y∈L(A;ε). 故L(A;ε)是S的子代数.
定理2设A是S的一个非空犹豫模糊子集,如果∀ε∈[λ,μ),L(A;ε):={hA(x)⊆ε|x∈S}非空,且L(A;ε)是S的子代数,则A是S的(λ,μ)-反犹豫模糊子代数.
证明假定存在x0∈S,使得hA(0)∩μ⊃hA(x0)∪λ,取ε=hA(x0)∪λ,则hA(x0)⊆ε,并且hA(0)⊃ε,λ≤ε<μ. 因为L(A;ε):={hA(x)⊆ε|x∈S}非空,且L(A;ε)是S的子代数,从而0∈L(A;ε),即hA(0)⊆ε与hA(0)⊃ε矛盾,因此对∀x∈S,有hA(0)∩μ⊆hA(x)∪λ.
假定x0,y0∈S,有hA(x0*y0)∩μ⊆hA(x0)∪hA(y0)∪λ成立,令ε=hA(x0)∪hA(y0)∪λ,则有hA(x0)⊆ε,hA(y0)⊆ε,hA(x0*y0)∩μ⊃ε,因此hA(x0*y0)⊃ε. 由于x0,y0∈L(A;ε),且L(A;ε)是S的子代数,所以x0*y0∈L(A;ε), 这与hA(x0*y0)⊃ε矛盾. 因此对∀x,y∈S,有hA(x*y)∩μ⊆hA(x)∪hA(y)∪λ.
所以,根据定义6 可知A是S的(λ,μ)-反犹豫模糊子代数.

定理4设A和B都是S的(λ,μ)-反犹豫模糊子代数,则A∪B也是S的(λ,μ)-反犹豫模糊子代数.
证明因为A和B都是S的(λ,μ)-反犹豫模糊子代数,所以∀x,y∈S,0≤λ<μ≤1,那么有hA(0)∩μ⊆hA(x)∪λ,hA(x*y)∩μ⊆hA(x)∪hA(y)∪λ;hB(0)∩μ⊆hB(x)∪λ,hB(x*y)∩μ⊆hB(x)∪hB(y)∪λ.
于是hA∪B(x)∪λ=hA(x)∪hB(x)∪λ=(hA(x)∪λ)∪(hB(x)∪λ)⊇(hA(0)∩μ)∪(hB(0)∩μ)=(hA(0)∪hB(0))∩μ=hA∪B(0)∩μ,hA∪B(x*y)∩μ=hA(x*y)∪hB(x*y)∩μ=(hA(x*y)∩μ)∪(hB(x*y)∩μ)⊆(hA(x)∪hA(y)∪λ)∪(hB(x)∪hB(y)∪λ)=(hA(x)∪hB(x))∪(hA(y)∪hB(y))∪λ=hA∪B(x)∪hA∪B(y)∪λ.
因此A∪B也是S的(λ,μ)-反犹豫模糊子代数.

定理5设S1和S1是两个N(2,2,0)代数,f:S1→S2为同态映射且f(0)=0.B是S2的(λ,μ)-反犹豫模糊子代数,则f-1(B)是S1的(λ,μ)-反犹豫模糊子代数.
证明∀x1,y1∈S1,因为f:S1→S2为同态映射,且B是S2的(λ,μ)-反犹豫模糊子代数,所以hf-1(B)(x1*y1)∩μ=hB(f(x1*y2))∩μ=hB(f(x1)*f(y1))∩μ⊆hB(f(x1))∪hB(f(y1))∪λ=hf-1(B)(x1)∪hf-1(B)(y1)∪λ.
又因为x∈S1,B是S2的(λ,μ)-反犹豫模糊子代数,因此有hf-1(B)(0)∩μ=hB(f(0))∩μ⊆hB(f(x))∪λ=hf-1(B)(x)∪λ,故f-1(B)是S1的(λ,μ)-反犹豫模糊子代数.
定理6设S1和S1是两个N(2,2,0)代数,f:S1→S2为同态映射且f(0)=0,A是S1的(λ,μ)-反犹豫模糊子代数,则f(A)是S2的(λ,μ)-反犹豫模糊子代数.
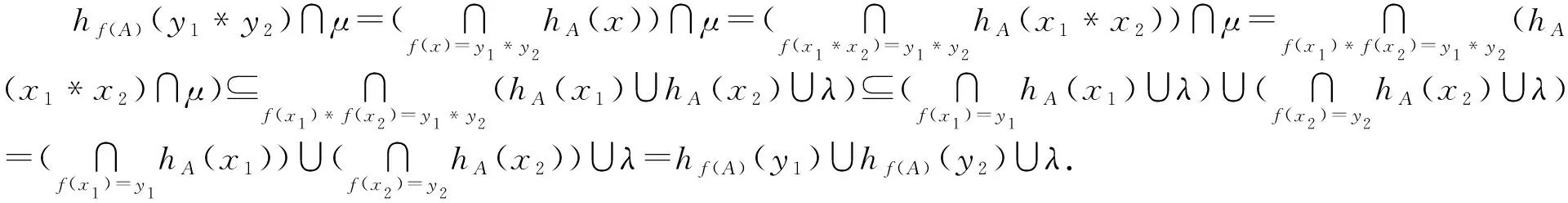

定义7设A,B分别是非空集合S1,S2的犹豫模糊子集,对∀(x,y)∈S1×S2,定义映射A⊗B:S1×S2→P([0,1]),其中hA⊗B(x,y)=hA(x)∪hB(y),则A⊗B是S1×S2的犹豫模糊子集,并称A⊗B为A和B的反直积.
定理7如果A和B分别是N(2,2,0)代数S1和S2的(λ,μ)-反犹豫模糊子代数,则A⊗B也是N(2,2,0)代数S1×S2的(λ,μ)-反犹豫模糊子代数. 其中规定∀(x1,y1)∈S1×S2,则(x1,y1)*(x2,y2)=(x1*x2,y1*y2),(x1,y1)Δ(x2,y2)=(x1Δx2,y1Δy2).
证明∀(x,y)∈S1×S2,因为A和B分别是S1和S2的(λ,μ)-反犹豫模糊子代数,有hA⊗B(0,0)∩μ=(hA(0)∪hB(0))∩μ=(hA(0)∩μ)∪(hB(0)∩μ)⊆(hA(x)∪λ)∪(hB(y)∪λ)=(hA(x)∪hB(y))∪λ=hA⊗B(x,y)∪λ.
对∀(x1,y1),(x2,y2)∈S1×S2,由于A和B分别是N(2,2,0)代数S1和S2的(λ,μ)-反犹豫模糊子代数,因此有hA(x1*x2)∩μ⊆hA(x1)∪hA(x2)∪λ,hB(y1*y2)∩μ⊆hB(y1)∪hB(y2)∪λ,hA⊗B((x1,y1)*(x2,y2))∩μ=hA⊗B(x1*x2,y1*y2)∩μ=(hA(x1*x2)∪hB(y1*y2))∩μ=(hA(x1*x2)∩μ)∪(hB(y1*y2)∩μ)⊆(hA(x1)∪hA(x2)∪λ)∪(hB(y1)∪hB(y2)∪λ)=hA⊗B(x1,y1)∪hA⊗B(x2,y2)∪λ.
所以A⊗B是S1×S2的(λ,μ)-反犹豫模糊子代数.

