最优外插Jacobi信号检测算法

许耀华,丁梦琴,蒋 芳,王 翊

(安徽大学 电子信息工程学院, 安徽 合肥 230601)

大规模多输入多输出(multiple input multiple output, 简称MIMO)极大地提高了系统容量和频谱利用率，已成为无线通信的重要技术之一[1].大规模 MIMO系统数量较多的天线给信号检测带来巨大挑战[2].信号检测算法中，最大似然检测算法性能最优，但其复杂度会随着发射天线数量的增加呈指数级增长，其最优性能在实际应用中难以实现[3].线性检测类算法，能实现近似最优的检测性能，但这类算法需矩阵求逆，复杂度高达O(K3)(K为发射天线数量)[4].为了避免复杂的矩阵求逆、降低复杂度，研究人员提出了一系列低复杂度检测算法[5-7].文献[8]提出一种基于Neumann级数展开的最小均方误差信号检测算法，当展开阶数小于3时，算法矩阵求逆复杂度较低，但当展开阶数大于3后，算法矩阵求逆复杂度变得很高.文献[9]对共轭梯度检测算法进行改进，改进后的算法收敛速度较快.文献[10]提出Jacobi迭代检测算法，该算法的复杂度较低，但收敛速度慢.文献[11]提出阻尼Jacobi(damped Jacobi, 简称DJ)算法，在Jacobi算法的迭代过程中引入阻尼参数，DJ算法的复杂度低于Jacobi算法的复杂度.

针对最小均方误差(minimum mean square error，简称MMSE)信号检测算法复杂度较高、传统Jacobi(conventional Jacobi, 简称CJ)算法收敛速度慢的问题，该文基于外插因子[12]提出最优外插Jacobi (optimal extrapolation Jacobi, 简称OEJ)信号检测算法，以降低算法复杂度、提高收敛速度.

1 系统模型

该文采用的大规模MIMO系统，是一个单基站多用户系统，由一个配备N根天线的基站和K个单天线用户组成，其中N≫K.基站接收的信号[4]为

y=Hx+n,

(1)

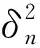
2 信号检测算法

2.1 Jacobi信号检测算法

MMSE信号检测算法是传统信号检测算法之一，在发射天线数远小于接收天线数时，可获得近似最优的检测性能.随着发射天线数量的增加，矩阵求逆的复杂度逐渐提高，MMSE信号检测算法的复杂度也越来越高.Jacobi信号检测算法避免了矩阵求逆，将信号检测问题转变为线性方程组的求解，降低了信号检测算法的复杂度.

MMSE信号检测算法中的关键表达式[10]为

(2)

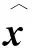
Jacobi信号检测算法将滤波矩阵W分解为对角矩阵D、上三角矩阵L和下三角矩阵U之和，即

W=D+L+U，

(3)

其中：L=UH.Jacobi信号检测算法第t次迭代的估计信号[10]为

(4)

其中：t为迭代次数.

在大规模MIMO系统中，当用户数远小于基站侧天线数时，矩阵W是对角占优矩阵，Jacobi信号检测算法收敛[13].

2.2 OEJ信号检测算法

2.2.1 OEJ信号检测算法

为降低信号检测算法的复杂度，提升信号检测算法的收敛速度，该文基于外插因子ωt，提出OEJ信号检测算法.

为了提高Jacobi信号检测算法的收敛速度，使每次迭代均获得更接近最优解的解，需在下一次迭代时保留一定比例的当前解[14].引入外插因子ωt动态调节保留的当前解比例.OEJ信号检测算法第t+1次迭代解的表达式[12]为

(5)

其中

(6)

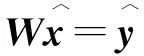
(7)

信号检测算法的性能最好，故最优ωt可通过下式求得

(8)

解(8)式，可得

(9)

OEJ信号检测算法的步骤如下：

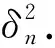
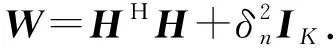
(3)D=diag(W).

(4)F=D-W.

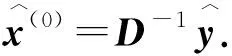
(7) forn=0:t-1.

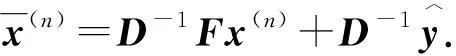
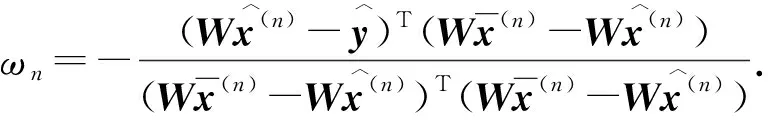
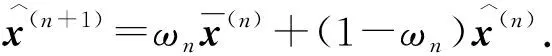
2.2.2 复杂度分析

3 仿真实验

为验证OEJ信号检测算法的性能，将其与DJ，CJ，MMSE信号检测算法进行对比.在MATLAB平台上进行仿真实验，传输信道为瑞利衰落信道，调制方式为16-QAM调制.图1和2分别给出K=16，N=128和K=16，N=64时4种算法的误码率.

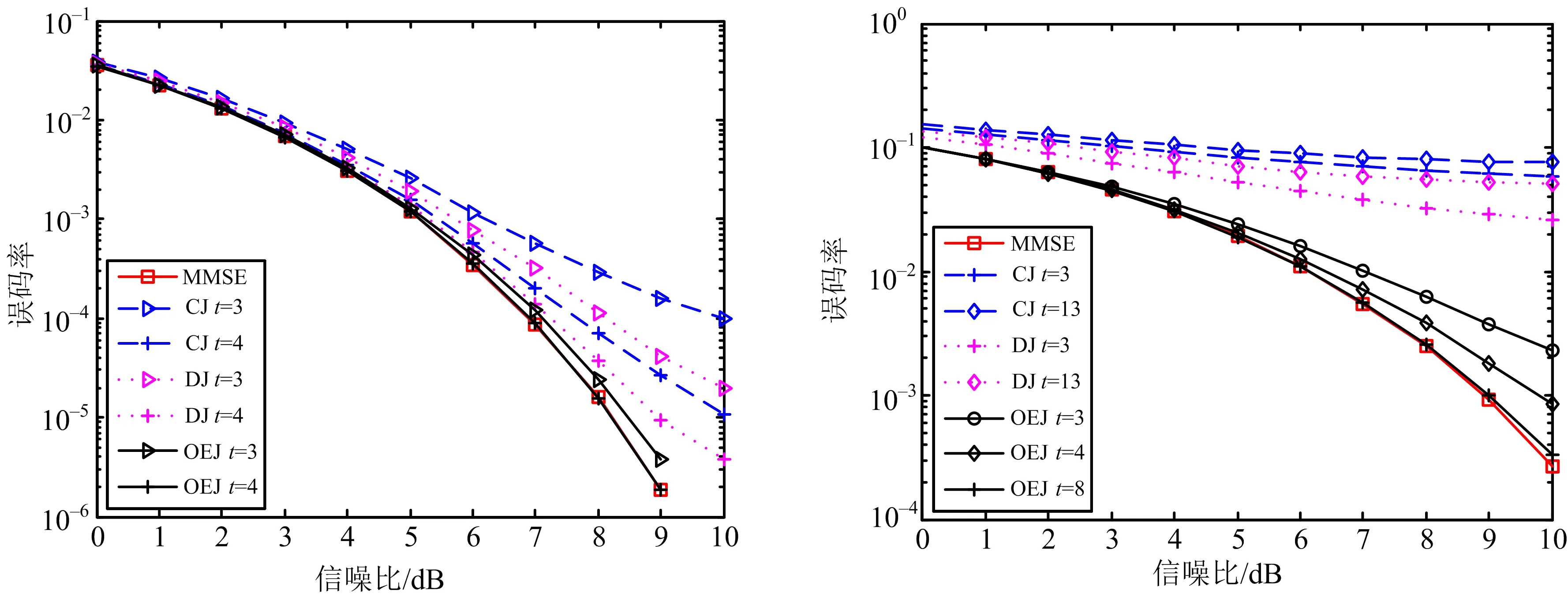
图1 K=16，N=128时4种信号检测算法的误码率 图2 K=16，N=64时4种信号检测算法的误码率

由图1可知：当迭代次数为3时，OEJ信号检测算法的误码率明显低于CJ，DJ信号检测算法；当迭代次数为4时，OEJ，CJ，DJ信号检测算法的误码率均降低，但OEJ信号检测算法的误码率仍低于CJ，DJ算法的误码率；迭代次数为4时的OEJ信号检测算法的误码率曲线与MMSE算法的误码率曲线完全重合，表明OEJ信号检测算法具有近似最优的检测性能.

由图2可知：CJ，DJ信号检测算法的误码率均较高，CJ算法迭代13次时的误码率反而高于迭代3次时的误码率，DJ算法在信噪比为10 dB、迭代次数为13次时的误码率高达0.02；OEJ信号检测算法误码率随迭代次数的增加而降低，8次迭代后的误码率非常接近MMSE算法.对比图1，2可知，OEJ，CJ，DJ信号检测算法在基站天线数与用户数比值较大时误码率较低，但当该比值变小时，3种信号检测算法的误码率均出现不同幅度的升高，CJ和DJ算法误码率升高的幅度较大，OEJ算法误码率升高的幅度较小， OEJ算法8次迭代后仍可获得较低的误码率，表明CJ和DJ算法均不适用于基站天线数与用户数比值较小的场景，而OEJ算法则可以.

图3为用户数为16、基站天线数为128、信噪比为9 dB时3种算法的误码率随迭代次数变化的情况.

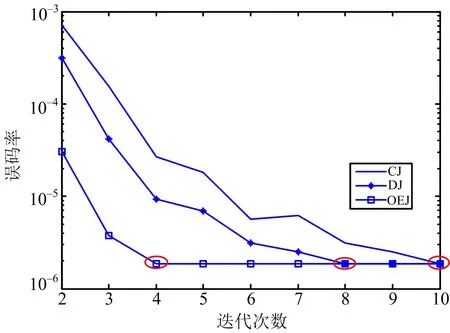
图3 误码率与迭代次数的关系曲线

由图3可知，相对于CJ，DJ信号检测算法，该文提出的OEJ信号检测算法随迭代次数的增加误码率减小最明显、收敛最快.

4 结束语

该文基于外插因子，提出了OEJ信号检测算法.复杂度分析及仿真实验结果表明：OEJ信号检测算法的复杂度为O(K2)，比MMSE信号检测算法的复杂度低一个数量级；相对于CJ和DJ信号检测算法，OEJ信号检测算法的误码率最低，随迭代次数的增加误码率减小最明显、收敛最快；迭代次数为4时的OEJ信号检测算法具有近似最优的检测性能； CJ和DJ算法均不适用于基站天线数与用户数比值较小的场景，而OEJ算法则可以.因此，该算法可作为大规模MIMO系统的低复杂度信号检测的有效算法.