方程的可解性

李昌吉

(阿坝师范学院 藏汉双语学院，四川 汶川 623002)

数论学家F.Smarandache在其《Only Problems,Not Solution》一书中定义了Smarandache函数S(n)和伪Smarandache无平方因子函数Zω(n).Smarandache函数S(n)=min{m∈+|n|m!}表示使n|m!成立的最小正整数m，伪Smarandache无平方因子函数Zω(n)表示最小的正整数m,使得n|mn，即Zω(n)=min{m∈+|n|mn}.很多学者对函数S(n)和Zω(n)的性质进行了研究，如文献[1-5].文献[6]研究了方程的可解性.文献[7-9]研究了方程φ(n)的可解性.文献[10]研究了方程φ(n)=S(nk)或σ(2αq)/S(2αq)的可解性.文献[11]研究了方程Zω(φ(n))=φ(Zω(n))和Zω(n)+φ(n)=2n的可解性等.论文将研究数论函数方程

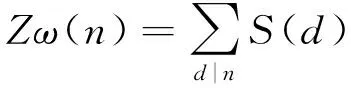
(1)

的可解性，结合Zω(n)函数和S(n)函数的性质，利用初等方法给出了方程(1)在一些情况下的解的情况.

1 引 理

S(n)=max{S(p1a1),S(p2a2),…,S(pkak)}.

引理3[13]对于素数p和正整数k，有(p-1)k+1≤S(pk)≤kp；如果k

引理4[14]设a与m是整数，gcd(a,m)=1，则存在无穷多个素数p，满足p≡a(modm).

2 定理及其证明

定理1当n仅有一个素因子或无平方因子时，方程(1)无正整数解.

证明当n仅有一素因子，设n=pa，a≥1，此时Zω(n)=p，而

有

此时方程(1)无解.

当p1=2时，有

而Zω(n)≡0(mod2)，此时方程(1)无解.

当p1≠2，k=2时，有

此时方程(1)无解.

当p1≠2，k≥3时，有

此时方程(1)无解.

定理2当n含有平方素因子且仅有两个素因子时，方程(1)有无穷多组正整数解.

证明设n=paqb，(p,q)=1，p>q，则若q=2，即n=pa2b，b≥1，有

此时方程(1)无解.

若p≤a，则

即

此时方程(1)无解.

若n=pqb，q>b≥2，且S(n)=S(p)，则

方程(1)化为

即

(2)

当b≡0(mod4)时，有

p(q-b-1)≡0(mod2)，

此时方程(1)无解.

当b≡1(mod4)时，有

p(q-b-1)≡1(mod2)，

此时方程(1)无解.

当b≡2(mod4)，b≡3(mod4)时，对b进行讨论：当b=2时，方程(2)化为1+3q=p(q-3)，所以2≤q-3<3，易知此时方程(1)无解.当b=3时，方程(2)化为1+6q=p(q-4)，所以1≤q-4<6，易知此时有p=31，q=5，经检验，n=31·53是方程(1)的解.

同理，对b≤100进行计算检验，得到方程(1)的解有：n=31·53，103·117，499·1914，1601·2923，23 311·3735，31 981·4139，32 713·6762，17 333·7162，9 643·7962，7 177·8963，90 703·7370，15 199·10983，340 693·8987，216 553·9794，75 161·10194，57 487·10394.

由引理5知满足条件的素数p有无穷多个，所以方程(1)有无穷多解.

若n=paq，p>a≥2，此时有S(n)=S(pa)，则

方程(1)化为1+q+pa(a+1)=pq，而1+q+pa(a+1)≡0(mod2)，pq≡1(mod2)，所以此时方程(1)无解.

若n=paqb，p>a，q>b≥2，t=max{a,b}，则

即

同理，有

即

所以，有

故方程(1)有解的必要条件之一是

综上，定理2得证.

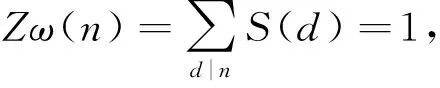
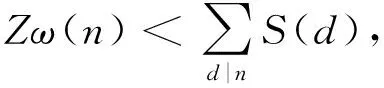
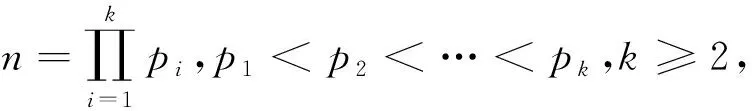
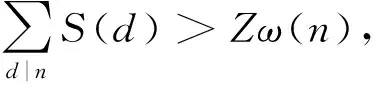
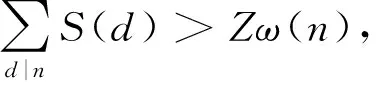
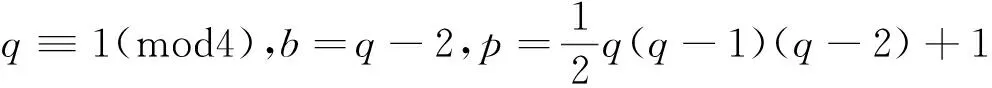
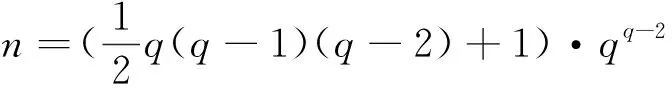
3 结束语