拓展验证方法 学会理性思考
□孙保华
荷兰数学教育家弗赖登塔尔说:“真正的数学家常常凭借数学的直觉思维做出各种猜想,然后加以证实。”因此,教师要鼓励学生提出猜想并积极验证,增强主动探究、获取数学知识的能力,促进学生创新思维的发展。在实际教学中,教师要根据学生的年龄特点和活动经验尝试从不同的角度,拓展验证的方法,培养学生严谨的思维方式。
一、片面与全面——取长补短
小学数学中有归纳数学规律的学习。教学中,教师通常会先呈现几个具体例子让学生进行猜想,再让学生自主举几个例子来验证。如果学生举的例子可能导致得出错误的结论,那么教师有必要对这种枚举验证进行优化。在枚举验证时,要考虑的不在于例子的个数,而在于例子的类型。因此在教学中,教师要引导学生全面地思考问题,验证时要从多种类型、多个角度来举例子,说明猜想的正确性。请看以下教学片段。
在教学完乘法口诀后,教师出示如下三组不等式。
3×7>3+7 3×8>3+8 3×9>3+9
师:请同学们仔细观察这三组不等式,你有什么发现?
生:我发现3×7的积21大于3+7的和10。
生:我发现3×9的积27大于3+9的和12。
生:从这三个不等式中我发现两个数的乘积大于这两个数的和。
师:大家都有一双会发现的眼睛。是的,在这儿两数之积大于这两个数之和。请大家再举例验证一下。
生:5×6>5+6,5×7>5+7,5×8>5+8。
生:4×5>4+5,4×8>4+8,4×9>4+9。
……
很多教师一般教学到此为止,不再引导学生继续思考。这里学生举的例子只是一些同类型的不等式,那么其他有关的不等式是否也有这样的规律呢?因此在学生枚举验证时,教师要及时进行引导与纠正,要强调例子的类型,而不只是盲目地举例。
师:这个猜想正确吗?这里只是列举了一些同类型的不等式。同学们可以再举一些与特殊数相关的不等式,如与0、1、2有关的不等式来验证我们提出的猜想。
生:0×7<0+7,0×9<0+9,0×6<0+6,我发现与0有关的不等式两数之积小于两数之和,与我们刚才的猜想正好相反。
生:1×5<1+5,1×7<1+7,1×8<1+8,我发现与1有关的不等式两数之积小于两数之和,与我们刚才的猜想也正好相反。
生:2×1<2+1,2×2=2+2,2×3>2+3,2×4>2+4……我发现与2 有关的不等式,另一个乘数等于1时两数之积小于两数之和,另一个乘数等于2时两数之积与两数之和相等,另一个乘数是3时两数之积大于两数之和。
师:通过进一步举例,你们认为我们刚才的猜想还正确吗?看来,举例子验证的时候,要找不同类型的例子。
当学生只举出一些同类型的例子时,教师要及时进行点拨,引导学生发现规律。如当学生举出与0、1有关的不等式时,发现的规律与之前的猜想正好相反;当学生举出与2 有关的不等式时,发现有三种不同的情况。通过这样的教学活动,学生发现举例需要全面考虑,要举出不同的类型,甚至发现只要举出一个反例就能推翻之前的猜想。
二、枚举与推理——相辅相成
在枚举验证过程中,教师要引导学生全面地思考问题,要从多种类型、多个角度来进行分类举例,同时所举的例子要具有一定的代表性和典型性。如此仍不能保证前期的猜想一定是正确的。因此教师可以引领学生向推理验证转变,让学生经历推理过程,进一步来验证猜想的可靠性,提升学生思维的深刻性。
例如,苏教版教材四年级下册“加法交换律和结合律”的教学。
生:交换两个加数的位置,和不变。
师:这只是一个猜想,那么这个猜想到底对不对呢?还需要我们进一步验证。你们认为可以怎样进行验证?
生:再举一些例子,看是不是都符合“交换两个加数的位置,和不变”的规律。
师:请同学们在研究单上再写三个这样的等式。想一想这样的等式有怎样的规律。
生:3+5=5+3,24+27=27+24,126+213=213+126。
生:0+15=15+0,13+1=1+13,1+0=0+1。
生:0.6+0.2=0.2+0.6,0.3+0.5=0.5+0.3,0.4+0.3=0.3+0.4。
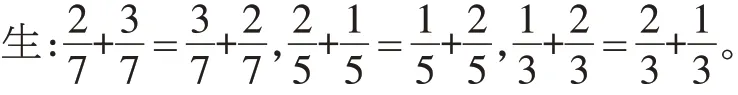
……
生:我发现不管是整数,还是小数和分数,交换两个加数的位置,它们的和都不变。
师:瞧,这些同学举的例子可真丰富,有整数的例子,有小数和分数的例子,还有与0有关的例子,它们相加的和都不变。这样的例子能列举得完吗?
生:不能。
师:有哪位同学找到交换两个加数的位置之后和不相等的例子吗?
生:没有。
师:同学们举的例子各不相同,但得到的规律是一致的。其实,我们也可以用线段图来表示加法交换律。
(教师出示线段图,如图1)
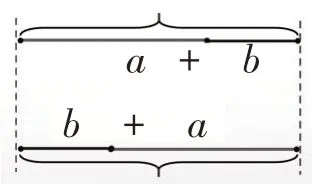
图1
师:谁来说说示意图表示的意思?
生:第一条长线段可以用a+b表示,交换a、b两条线段的位置,第二条长线段可以表示为b+a。
生:交换位置以后这两条长线段的总长度没有变化。也就是交换两个加数的位置,它们的和不变。
当学生提出猜想后,教师及时让学生进行举例验证。学生举出的例子有整数、小数和分数,还有与0有关的特殊例子,分类举出一些例子且具有一定的代表性。同时学生举不出反例。教师并没有满足于此,继续引导学生用数形结合的方式进行推理验证,这种从特殊例子到一般表达进一步确保了猜想的正确性,促进了学生思考问题的完整性。
三、操作与推理——相得益彰
虽然学生可以通过操作,在具体感知和直接观察中验证猜想,但测量、撕拼、折拼等操作实验不可避免地会存在误差,这是操作验证的局限性。如何弥补这种局限性?教师应该寻求更严密更科学的验证方法。可以把已知的对象进行转化和推理,经历从操作验证到推理验证的思维跨越,提升学生思维的缜密性和深刻性。
例如,苏教版教材四年级下册“三角形的内角和”的教学。
师:请同学们任选一个直角三角形,测量三个内角的度数,再算一算内角和是多少。
(学生进行测量并计算)
师:直角三角形的内角和是多少度?
生:直角三角形的内角和是180°。
师:有没有不是180°的?
生:我量的这个三角形三个角的度数和是182°。
生:我量的这个三角形三个角的度数和是177°。
生:测量会出现误差。
师:有同学提出把直角三角形的三个角取下来合在一起,可以怎样操作呢?
生:把三角形的三个角撕下来可以拼成一个平角,也就是180°。(边说边操作)
师:三角形的三个内角可以拼成一个平角,说明这个直角三角形的内角和是180°。能不能不破坏原来的三角形,直接把三个角拼在一起呢?
生:我是沿着两条边的中点折第一个角,其他两个角的顶点与第一个角的顶点重合,正好折成一个平角,也就是180°。
生:我这个折出来角与角之间有空隙,好像比一个平角大一些。
师:刚才我们采用的折拼的验证方法可能存在误差,有没有更加严谨、巧妙的验证方法呢?老师这里有一张长方形的纸,你能想到什么?
生:长方形对边相等,四个角都是90°。
生:可以沿着长方形的对角线对折,分成两个完全相同的直角三角形。
师:真会动脑筋,分成了两个完全相同的直角三角形。现在同学们能不能根据长方形的内角和来证明直角三角形的内角和呢?
生:因为我们是把一个长方形平均分成了两个完全相同的直角三角形,两个直角三角形的内角和正好等于这个长方形的内角和,所以只要用90°×4÷2=180°就可以得到一个直角三角形的内角和。
师:看来通过推理也能验证直角三角形的内角和是180°。
学生用量、撕、折、拼的方法探索直角三角形的内角和,这些验证方法都是属于操作层面的,存在着一定的误差。因此教师可以引导学生寻求更加严谨的验证方法,利用长方形的特征来推导直角三角形的内角和。通过这样的推理验证会使结论更具一般性和科学性。
四、抽象与形象——有机结合
在验证环节,很多教师喜欢带领学生用严密的演绎推理来验证猜想。这些严密的演绎推理很多是全符号的,这样的验证虽然短小精悍但很抽象,学生不易接受。根据学生的年龄特点,教师可以对验证过程进行改造,用“形象”化的演绎推理来验证猜想。这一验证过程将一些非本质的东西进行改造使其形象化,既保持了演绎推理中原本所蕴含的逻辑关系和相对严谨的思维过程,又让学生充分理解了验证过程,加深了对知识的理解。
例如,苏教版教材五年级下册《和与积的奇偶性》的教学。
师:奇数与奇数的和是奇数还是偶数?请同学们任意找两个奇数,把它们相加,观察结果说说你的发现。
生:我用3+5=8,7+9=16,5+7=12,发现两个奇数相加的和是偶数。
生:我用111+213=324,123+17=140,23+13=36,同样发现两个奇数相加的和是偶数。
……
师:两个奇数相加的和是偶数,这只是我们的一个猜想,如何来验证这一猜想呢?
教师引领学生经历严密的演绎推理,验证过程如下。
证明:假设这两个奇数分别是a=2k1+1,b=2k2+1,那么a+b=2k1+1+2k2+1=2k1+2k2+2=2(k1+k2+1),所以2(k1+k2+1)是一个偶数,即a 加b 的和是一个偶数。
这是一个严密的代数推理验证,学生需要理解奇数与偶数的代数式,还要对用字母表示的代数式进行恒等变形,并通过变形后的代数式进行奇偶性判断。这种符号化的代数推理很有数学味,但不符合小学生的认知水平。教师需要对验证过程进行改造,将奇数与偶数的代数式表示进行直观化,变成让学生能充分理解的方式,将原本抽象的代数推理过程形象化。
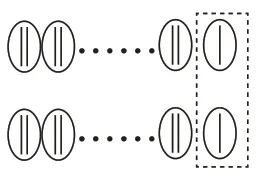
奇数和偶数的代数式表示用图形来直观化,这种“形象”化的逻辑推理,大大降低了学生理解的难度,同时也能达成一个相对严谨的思维过程,更有利于培养学生的抽象思维能力。
真正的数学教学不仅只停留在通过归纳和类比得到猜想,更应该在验证环节予以重视。如果猜想是学生数学思维发展的风帆,那验证就是轻舟前行的双桨,只有扬起风帆撑起双桨,才能让学生在数学的海洋中畅游。

