（三年级）如何用好习题巩固“周长”和“面积”

□许玉燕

“周长”和“面积”是两个抽象且内涵丰富的数学概念，在实际教学中学生很容易对它们的概念和计算方法产生混淆。在练习课中可通过合理设计习题，促进学生对“周长”和“面积”关系的辨析。

一、“源”题分析，小“材”大“用”

在长方形的面积教学后，教材编排了这样一道习题（如图1）。通过让学生比较剩下部分的周长与面积，进一步巩固相关概念。知道面积相等的图形，周长不一定相等。

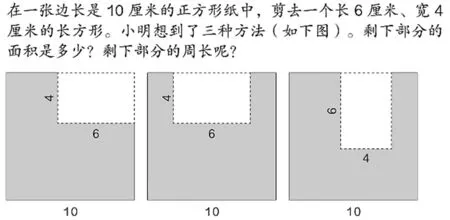
图1

在实际教学中，教师不妨给这道习题动个“小手术”，更好地将知识本质与学生思维联结起来。

1.出示要求，明确题意

在边长为10 厘米的正方形纸中，沿着它的边剪去一个长6 厘米、宽4 厘米的长方形，可以怎样剪？再算一算余下图形的周长是多少，你有什么发现？

提示：可以将长方形纸片，在正方形格子纸上“摆一摆”代替“剪一剪”。

2.交流汇报，说说想法

预设可能出现的情况：学生动手操作探索，并通过计算发现剪法③的周长最长（如图2）。

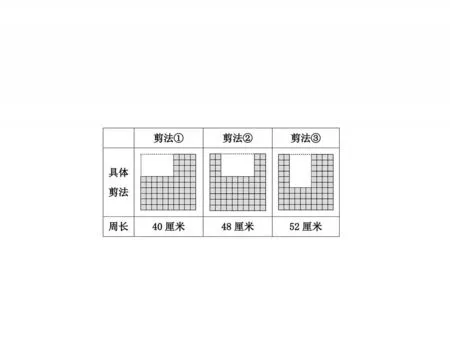
图2

交流小结：有两种剪法，第一种，剪去的长方形在角上，第二种，剪去的长方形在边上。第二种剪法又分为两种情况，一种情况“长”在边上，另一种情况“宽”在边上。要让剪去的边最短，这样加上的边才会更长，才能使余下图形的周长最长。

3.计算反思，发现规律

教师提问：通过对图2中图形周长和面积的比较，有什么发现？引导发现：无论是哪一种剪法，面积相等的图形，周长不一定相等。

二、“源”题改造，别出心裁

1.出示题目，动手操作

在边长是10 厘米的正方形纸中剪去一个周长是16 厘米的长方形或正方形（边的长度是整厘米数），要使余下图形的面积最小，应该剪去怎样的一个图形？请你在下面的正方形中先“画一画”表示剪去，再算一算余下图形的面积。

让学生先独立思考，再在正方形纸上“画一画”，并计算余下图形的面积。

2.比较验证，交流总结

教师出示不同的三种剪法（如图3），引导学生进行比较验证。学生汇报交流：因为周长相等的长方形或正方形，正方形的面积最大，所以应该剪去边长4厘米的正方形，这样余下图形的面积才会最小。

图3

三、思维贯通，灵活应用

出示情境：张爷爷有一片边长10 米的正方形菜园，他想用12 米长的篱笆从菜园里围出一个长方形或正方形鸡舍（边的长度是整米数）。

（1）思考：鸡舍的形状有哪几种可能？

学生计算后得出：①长方形2 种：长5 米，宽1米；长4米，宽2米。②正方形1种：边长3米。

（2）请你根据要求帮张爷爷从以下几种方案中做选择（如图4）。

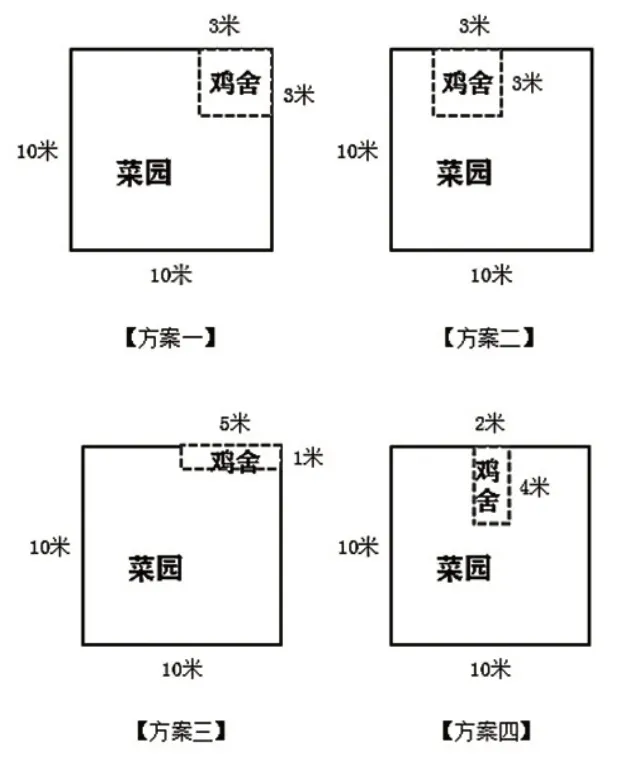
图4

①使剩下的菜园面积最大，应选择（ ）号方案。

②使剩下的菜园面积最小，应选择（ ）号方案。

③使剩下的菜园周长最长，应选择（ ）号方案。

④使剩下的菜园周长最短，应选择（ ）号方案。

以上教学在诊断学情、分析教材的基础上将习题进行分解、补充、重构，通过“化静为动”，让学生在观察、操作中找联系、辨差异，从而厘清“周长”与“面积”的概念本质及计算方法，加深了学生对周长和面积相关知识的理解和应用。