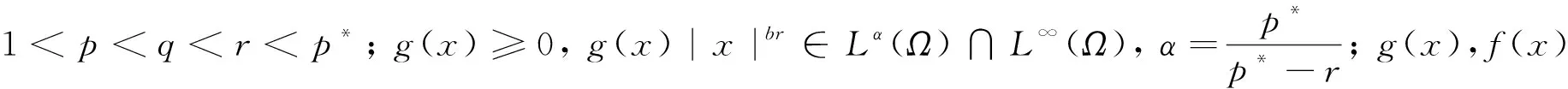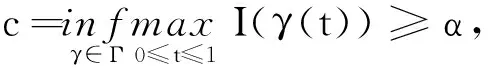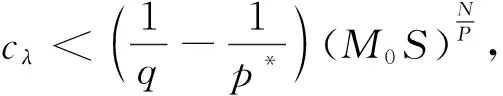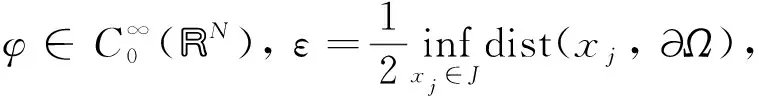拟线性Kirchhoff型问题解的存在性①
邹小林
西南大学 数学与统计学院,重庆 400715
考虑如下p阶Kirchhoff问题:
(1)


问题(1)有非局部项M(‖u‖p),因此问题(1)是一个非局部问题,与下面的Kirchhoff方程有关:
(2)
方程(2)由Kirchhoff提出,该方程推广了弹性弦自由振动的经典D′A lembert’s波动方程. 在之后,有许多学者对Kirchhoff方程进行了研究,可以参见文献[1-4].
对于带有狄利克雷边界条件的临界Kirchhoff问题,可以参见文献[5-7]. 特别地,文献[8]用变分方法研究了如下问题解的存在性和多解性:
其中
M(t)=a+btm
并且λ>0,a>0,b>0,p(m+1) 文献[9]利用Nehari流形和纤维映射方法得到了下列问题弱解的多解性: 这里M(s)=a+bsk,其中a,b,k>0. 并且1 文献[10-12]研究了具有非线性边界条件的问题. 文献[13]利用集中紧性原理和山路引理研究了下列拟线性椭圆问题解的存在性和多解性: 受文献[13]的启发,我们考虑问题(1)解的存在性. 我们对Kirchhoff函数M作如下假设: 若u∈W1,p(Ω)满足 则称u是问题(1)的弱解. 定理1假设1 定义X=W1,p(Ω)为索伯列夫空间,相应的范数为 当r∈[p,p*)时,嵌入XLr(Ω)是紧的. 设S为嵌入XLp*(Ω)的最佳常数,即 问题(1)的能量泛函为 易得Iλ(u)∈C1(X,R),于是对∀φ∈X,有 引理1[14,定理2.8]设(X,‖·‖X)是实Banach空间,I∈C1(X,R)满足I(0)=0,并且: (i) 存在常数ρ,α>0,使得I|∂Bρ≥α; (ii) 存在e∈XBρ,使得I(e)<0. Γ={γ∈C1([0,1],X)|γ(0)=0,γ(1)=e} 引理2假设定理1的条件成立,则: (i) 存在常数α,ρ>0,使得‖u‖=ρ时,有Iλ(u)≥α; (ii) 存在e∈X,使得‖e‖>ρ,且Iλ(e)≤0. 证利用迹定理和索伯列夫不等式,存在C1>0,使得 由1 由引理2可知,泛函Iλ(u)满足山路定理的几何结构,从而存在(PS)cλ序列,其中 且 Γ={γ∈C[0,1]|γ(0)=0,γ(1)=e} 证取u0∈X使得‖u0‖Lp*=1,则有 从而存在tλ>0,使得 且tλ满足 事实上,{tλ}是有界的. 由条件(M2)有 (3) 不妨假设对λ>0,有tλ≥1. 从(3)式可以得到 若t0>0,可得 从而存在λ*>0,使得λ≥λ*, 证步骤1 证明(PS)cλ序列的有界性. (4) 则 因为δ∈(ξ,1],1 ‖un‖p⇀μ|un|p*⇀υ 这里μ,υ是非负有界测度,M(RN)是RN上的有界测度空间. 在至多可数的集J上,存在RN中的不相等的点族{xj∈Ω|j∈J},以及一个正数族{vj∈Ω|j∈J},使得 (5) 即 (6) 由{‖un‖}有界和勒贝格控制收敛定理以及迹定理,可得 (7) 由Hölder不等式可得 (8) (9) (10) 由Hölder不等式和迹嵌入定理,对r∈[p,p*),嵌入XLr(∂Ω)是紧的,可得 (11) 由(9)-(11)式和{M(‖un‖p)}是有界的,可得 (12) 在证明中将会用到下面不等式: (13) 其中C1p,C2p是与p有关的正数. 分为以下两种情况讨论: 情形1 当p≥2时,由(12),(13)式以及{un}在X中弱收敛,un⇀u,可得 情形2 当1 我们有 定理1的证明 通过引理4可知Iλ(u)满足(PS)cλ条件,由极大极小值原理可知,泛函Iλ在cλ处存在临界点uλ,由Iλ(uλ)=cλ>0,故uλ≠0.